Bubble Sort in C++

9 mins readComment

Updated on Feb 26, 2024 12:32 IST

Bubble Sort in C++ involves repeatedly stepping through the list, comparing adjacent elements and swapping them if they are in the wrong order. The pass through the list is repeated until the list is sorted. This algorithm is known for its simplicity but is inefficient for large datasets.

Bubble sort is a simple sorting algorithm that is easy to understand and implement. This algorithm repeatedly compares the adjacent elements in an array or list and swaps them if they are not in the correct order. This process continues until the entire array is sorted.

Table of Content

Algorithm and Pseudocode for Bubble Sorting Algorithm
Working of Bubble Sort Algorithm
Bubble Sort implementation in C++
Result of different Test Cases
Complexity Analysis of Bubble Sort
Real-life Example of Bubble Sort
Applications of Bubble Sort
Advantages of Bubble Sort
Limitations of Bubble Sort

Algorithm and Pseudocode for Bubble Sorting Algorithm

Let's talk about the pseudocode for the bubble sort. In this, we traverse the entire array using two for loops. The first loop starts from the 0^th index, and the next loop starts from the adjacent element. Inside the inner loop, adjacent elements are compared and swapped if their order is incorrect. As a result, at the end of each iteration of the outer loop, the largest element bubbles up at the end of the list.

Algorithm

Step 1: Take input of the number of elements and array from the user.

Step 2: Start the outer loop, which will iterate over the array.

Step 3: Inside it, start the inner loop, which will compare adjacent elements and perform swapping.

Step 4: The process will repeat until the array is sorted.

PseudoCode

Procedure bubbleSort(array, M)
	array - list of elements to be sorted
	M - size of the input array
begin
	for i = 0 to M-1 do
		for j = 0 to M-1-i do
			if array[j] > array[j+1] then
				swap array[j] and array[j+1]
			end if
		end for
	end for
end procedure

Copy code

Recommended online courses

Best-suited Project Management courses for you

Learn Project Management with these high-rated online courses

Project Management

IACT GlobalCertificate

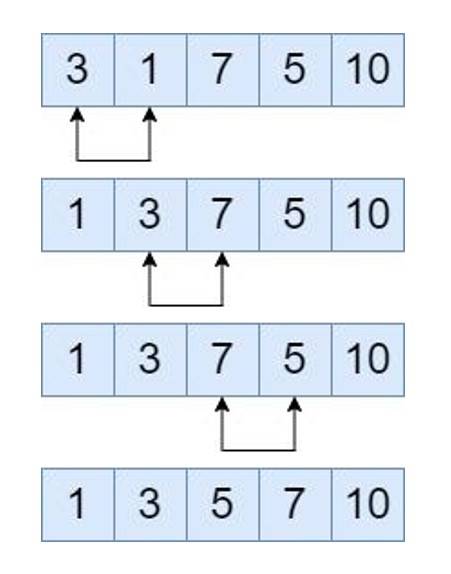
To understand the working of the bubble sort technique, let's take an example. Suppose an array of 5 elements [7, 3, 1, 10, 5] is given, and we need to sort. We use two for loops, the outer one will iterate over the array, and the inner loop will compare adjacent elements and perform swapping.

Iteration 1

Compare elements 7 and 3, swap them since 7>3, the new order is 3, 7, 1, 10, 5.
Compare elements 7 and 1, swap them since 7>1, the new order is 3, 1, 7, 10, 5.
Compare elements 7 and 10, not swap them since 7<10, the new order is 3, 1, 7, 10, 5.
Compare elements 10 and 5, swap them since 10>5, the new order is 3, 1, 7, 5, 10.

Iteration 2

Compare elements 3 and 1, swap them since 3>1, the new order is 1, 3, 7, 5, 10.
Compare elements 3 and 7, not swap them since 3<7, the new order is 1, 3, 7, 5, 10.
Compare elements 7 and 5, swap them from 7>5, the new order is 1, 3, 5, 7, 10

Iteration 3

Compare elements 1 and 3, not swap them since 1<3, the new order is 1, 3, 7, 5, 10.
Compare elements 3 and 5, not swap them since 3<5, the new order is 1, 3, 7, 5, 10.

Iteration 4

Compare elements 1 and 3, not swap them since 1<3, the new order is 1, 3, 7, 5, 10.

The input list is now sorted in ascending order.

Bubble Sort implementation in C++

The bubble sort approach can be implemented in any programming language. Below is its implementation in the C++ programming language.

/*
 * C++ Program to Implement Bubble Sort Approach
 */
 
#include <iostream>
 
using namespace std;
 
// The function will sort arry[] of size m using Bubble Sort.
void BubbleSort (int arry[], int m)
{
    int i, j;
    for (i = 0; i < m; ++i)
    {
        for (j = 0; j < m-i-1; ++j)
        {
            // Comparing consecutive elements and switching values when value at j > j+1.
            if (arry[j] > arry[j+1])
            {
                arry[j] = arry[j]+arry[j+1];
                arry[j+1] = arry[j]-arry[j + 1];
                arry[j] = arry[j]-arry[j + 1];
            }
        }
    }  
}  
 
// Main method
int main()
{
    int m, i;
    cout<<"\nEnter the total number of elements to be sorted: ";
    cin>>m;
 
    int arry[m];
    for(i = 0; i < m; i++)
    {
        cout<<"Enter element "<<i+1<<": ";
        cin>>arry[i];
    }
 
    // Call BubbleSort() function with arry[] of size m
    BubbleSort(arry, m);
 
    // Display the sorted array.
    cout<<"\nSorted Array is ";
    for (i = 0; i < m; i++)
    cout<<"->"<<arry[i];
 
    return 0;
}

Copy code

Program Explanation

The program takes input of the array and its size.
Next, it calls the BubbleSort() function with the array ‘arry’ and ‘m’ number of values as its arguments.
Implement the bubble sort using the nested for loop.
Loop 1 will iterate from 0 to m-1.
And Loop 2 will iterate from 0 to m-i-1.
The consecutive elements are compared and swapped if arry[j+1]<arry[j].
The flow then returns to the main function, and the sorted array is displayed.

Result of different Test Cases

Test Case 1: Best Case

Enter the total number of elements to be sorted: 5

Enter element 1: 9

Enter element 2: 20

Enter element 3: 69

Enter element 4: 290

Enter element 5: 2000

Sorted Array is ->9->20->69->290->2000

Test Case 2: Average Case

Enter the total number of elements to be sorted: 5

Enter element 1: 990

Enter element 2: 300

Enter element 3: 6

Enter element 4: 29

Enter element 5: 1200

Sorted Array is ->6->29->300->990->1200

Test Case 3: Worst Case

Enter the total number of elements to be sorted: 5

Enter element 1: 9908

Enter element 2: 3210

Enter element 3: 602

Enter element 4: 104

Enter element 5: 10

Sorted Array is ->10->104->602->3210->9908

Optimized Bubble Sort implementation in C++

In the above scenario, all comparisons are made even if the array has already been sorted. This increases the execution time of the algorithm. To solve this, we use an optimized approach; a new boolean variable swapped is introduced. Its value is set to be true if swapping of elements occurs; otherwise, it is false. When the swapped value becomes false, it signifies that the array is already sorted; there is no need to do further iterations.

/*
 * C++ Program to Implement Optimized Bubble Sort Approach
 */
 
#include <iostream>
 
using namespace std;
 
// The function will sort arry[] of size m using Bubble Sort.
void BubbleSort (int arry[], int m)
{
    int i, j;
    for (i = 0; i < m; ++i)
    {
        // Create boolean variable swapped and initialize it with false
        bool swapped = false;
        for (j = 0; j < m-i-1; ++j)
        {
            // Comparing consecutive elements and switching values when value at j > j+1.
            if (arry[j] > arry[j+1])
            {
                arry[j] = arry[j]+arry[j+1];
                arry[j+1] = arry[j]-arry[j + 1];
                arry[j] = arry[j]-arry[j + 1];
                // Its value becomes true if swapping takes place
                swapped = true;
            }
        }
        // Checking the value of swapped
        if(!swapped)
            break;
    }  
}  
 
// Main method
int main()
{
    int m, i;
    cout<<"\nEnter the total number of element to be sorted: ";
    cin>>m;
 
    int arry[m];
    for(i = 0; i < m; i++)
    {
        cout<<"Enter element "<<i+1<<": ";
        cin>>arry[i];
    }
 
    // Call BubbleSort() function with arry[] of size m
    BubbleSort(arry, m);
 
    // Display the sorted array.
    cout<<"\nSorted Array is ";
    for (i = 0; i < m; i++)
    cout<<"->"<<arry[i];
 
    return 0;
}
Copy code

Complexity Analysis of Bubble Sort

Now let's see the time and space complexity of bubble sort.

In the best-case scenario, bubble sort has a linear time complexity when the array is already sorted. Whereas, in average and worst-case scenarios, it has quadratic complexity when the array is unsorted.
The space complexity of bubble sort is constant, as it requires a small amount of additional space for storing temporary variables.

Cases	Time Complexity	Space Complexity
Best Case	O(n)	O(1)
Average Case	O(n²)	O(1)
Worst Case	O(n²)	O(1)

Real-life Example of Bubble Sort

Scenario: You are a teacher at Bubble Public School. It is time for morning assembly, and students must stand in ascending order of height, but your class students are standing randomly. There can be at most 20 students in a class. Your task as a teacher is to arrange the students in ascending order of their height.

Task: Implement an idea that allows the teacher to sort the students in ascending order on the basis of height.

Solution: Considering the size of the students, bubble sort is a reasonable choice because of its simplicity. The teachers can just swap the adjacent students, and the tallest student will be moved to the last on every pass.

Code:

#include <iostream>
using namespace std;

// Function to sort arr[] of size n using Bubble Sort.
void BubbleSort(int arr[], int n) {
    int i, j;
    for (i = 0; i < n; ++i) {
        for (j = 0; j < n - i - 1; ++j) {
            // Comparing consecutive elements and swapping if needed.
            if (arr[j] > arr[j + 1]) {
                // Using a temporary variable for swapping
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

// Main method
int main() {
    int n = 20; // Since there are 20 students
    // Array with the heights of all 20 students in centimeters
    int arr[n] = {100, 130, 99, 120, 80, 123, 102, 101, 122, 113, 95, 100, 132, 127, 85, 98, 122, 108, 96, 106};

    // Display the heights array before sorting.
    cout << "Height Array before sorting: ";
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";

    // Call BubbleSort() function
    BubbleSort(arr, n);

    // Display the sorted height array.
    cout << "\nHeight Array after sorting: ";
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";

    return 0;
}
Copy code

Output:

Height Array before sorting: 100 130 99 120 80 123 102 101 122 113 95 100 132 127 85 98 122 108 96 106

Height Array after sorting: 80 85 95 96 98 99 100 100 101 102 106 108 113 120 122 122 123 127 130 132

Applications of Bubble Sort

Bubble sort has its own set of applications, which are listed below:

Education: It is generally used for teaching sorting algorithms and basic programming concepts.
Small Datasets: It is suitable for sorting small arrays or limited datasets.
Testing: It can help in testing and verifying other sorting algorithms.
Understanding: It illustrates basic sorting principles like swaps and comparisons.

Advantages of Bubble Sort

Some advantages of using bubble sort are:

It is easy to understand and implement.
It requires no or a small amount of additional memory.
It can handle partially sorted and nearly sorted lists very efficiently.
It is simple to debug and helps in identifying and fixing issues.

Limitations of Bubble Sort

Below are the limitations of using bubble sort:

It is not suitable for large datasets, partially sorted arrays, or complex sorting tasks.
It is inefficient compared to other sorting algorithms and lacks stability in some scenarios.

Contributed By: Vansh

About the Author

Shiksha Online

This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio

Bubble Sort in C++

Algorithm and Pseudocode for Bubble Sorting Algorithm

Algorithm

PseudoCode

Best-suited Project Management courses for you

Project Management

Lean Six Sigma Green Belt Certification

Global Infrastructure Management Specialist

6 Month's Live Project Based Industrial Training on .NET / PHP Platform, with Placement Support

Live Project / Website Designing and Development Training Programme

Website Design and Development

Certificate in Software Corporate Training

Global Infrastructure Management Specialist (GIMS)

Industrial Research Program

Foundation Electronics

Working of Bubble Sort Algorithm

Bubble Sort implementation in C++

Program Explanation

Result of different Test Cases

Complexity Analysis of Bubble Sort

Real-life Example of Bubble Sort

Applications of Bubble Sort

Advantages of Bubble Sort

Limitations of Bubble Sort

Top Picks & New Arrivals