Central Limit Theorem

Introduction

Central limit theorem one of the most important and used theorem in statistics and data science, it is in the heart of Hypothesis testing. 

Being in the core of the data science and machine learning, it is quiet confusing.

So, in this we will briefly discuss Central limit Theorem, it’s , assumption and implementation in python.

Table of Content:

• Central Limit Theorem
• Mean and Standard Deviation of Sample Mean
• Assumption for Central Limit Theorem
• Implementation in Python

Central Limit Theorem

Then the distribution of the sample mean will be approximately normally distributed regardless of whether the population is normal or skewed.

Provided that sample size is sufficiently large (n > 30).

To know more about mean and variance read the article Measure of Central Tendency and Measures of Dispersion.

Confused! So let’s understand it through an example:

Mean and Standard Deviation of Sample Mean

Mean of the sample means:

Standard deviation of the sample means:

Assumptions

• Data must be randomly sampled
• Samples should be independent
• Sample size should be sufficiently large
  • When population is skewed, sample size should be large
  • When population is symmetric, sample size of 30 is sufficient
• Sample size should not be more than 10% of the population (when sampling is done without replacement)

Implementation in Python

Before directly going for python implementation, let’s understand the step by step process:

Let X be any random variable having finite mean and variance

1. Randomly pick m samples each of size n
2. Calculate the mean of each sample
3. Plot the distribution of m samples

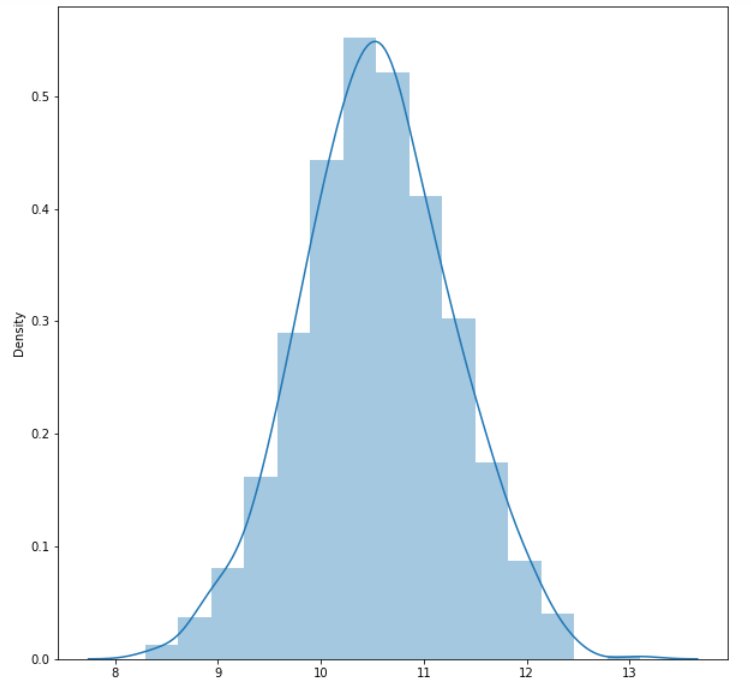
Let’s plot the normal distribution curve using CLT in Python

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# defining the sample size and number of samples we want to have
sample_size = 50
sample_number = 1000
sample_means = []
for i in range(0, sample_number):
    # randomly picking sample from the population distribution
    # In this case the population distribution is an Uniform distribution
    sample = np.random.uniform(1, 20, sample_size)
    sample_mean = sample.mean()
    sample_means.append(sample_mean)
 
plt.figure(figsize = (10, 10))
sns.distplot(sample_means, bins = 15);

Conclusion

In this article, we briefly explained CLT one of the most important and used theorem in statistics and data science.

Hope this article will help you in your data science and machine learning journey.