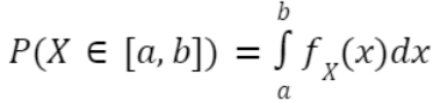PDF vs. CDF: Difference Between PDF and CDF
PDF describes the probability distribution of a continuous random variable, while PDF describes the probability distribution of both discrete and continuous random variables.
Discover the key difference between PDF and CDF. Understand how they shape data distribution and drive statistical analysis. Uncover the pivotal variance between these fundamental statistical concepts.
Best-suited Statistics for Data Science courses for you
Learn Statistics for Data Science with these high-rated online courses
The probability distribution of a random variable is a list of all possible outcomes with corresponding probability values, and different functions are used to describe this probability distribution. Probability Density Function and Cumulative Distribution Function are among such functions.
The probability Density Function describes the probability distribution of continuous random variables. The Cumulative Distribution Function deals with continuous and discrete random variables.
In this article, we will learn the difference between PDF and PDF in probability.
Must Explore – Statistics for Data Science Online Courses
Before starting the article, let’s discuss random variables.
A Random Variable is a numerical description of the outcome of a random experiment. Generally, it is represented by X.
It is of two types:
Discrete Random Variable: It has a countable number of values between two values.
Example: Number of Heads
Continuous Random Variable: It has an infinite number of values between two values.
Example: Distance Travelled
Now, let’s start with the probability density function vs cumulative distribution function based on the different parameters.
Table of Content
- PDF vs CDF
- What is Probability Density Function (PDF)
- What is Cumulative Distribution Function (CDF)
- Relation between PDF and CDF
- Key Difference between PDF and CDF
CDF vs PDF: Difference Between PDF and CDF
| Parameter | CDF | |
| Definition | PDF is the probability that a random variable (let X), will take a value exactly equal to the random variable (X). | CDF is the probability that a random variable (let X) will take a value less than or equal to the random variable (X). |
| Variable | Applicable only for Continuous Random Variable. | Applicable for both continuous and discrete random variables. |
| Value | The value lies between 0 and 1. | The value of CDF is always non-negative. |
| Formula | P (a <= X <= b) = F(b) – F(a) | FX(X) = P (X<= X) |



What is the Probability Density Function
A probability density function (PDF) is a fundamental concept in probability theory and statistics. It is used to describe the probability distribution of a continuous random variable. The PDF represents the likelihood of the random variable taking on a specific value or falling within a particular range of values. Mathematically, the PDF is a function that, when integrated over a range, gives the probability that the random variable falls within that range. It is a crucial tool for understanding and analyzing continuous probability distributions in various scientific and engineering fields.
- It tells the probability that a random variable takes on a certain value.
Must Read: Probability Density Function
Your Career Awaits: Discover the Best Government Job-Oriented Courses After 10 & Online Government Certification Opportunities
Formulas
The Probability density function of a continuous random variable X is a function fX: R -> [0, inf) such that:
Where R is a real number.



Properties
- The value of PDF is always greater than or equal to 1.
- The area under the PDF curve is always equal to 1.
- The median divides the PDF curve into two equal halves.



Example
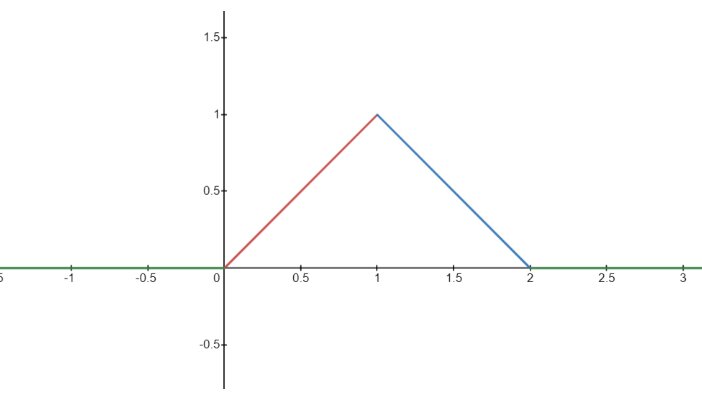
If
f(x) = x, if 0 < x < 1
f(x) = 2 – x, if 1 < x < 2 and
f(x) = 0, otherwise
Then, f(x) is a probability density function centred at x = 1.
What is the Cumulative Distribution Function?
A cumulative distribution function (CDF) is a function that gives the probability that a random variable is less than or equal to a certain value. In other words, it provides the cumulative probability of the random variable taking on a value less than or equal to a given value. The CDF is an essential concept in probability theory and statistics and is widely used to analyze and understand the behaviour of random variables.
Formula
The CDF (Cumulative Distribution Function) of a random variable X is defined as
FX(X) = P (X <= X),
for all x in R.



Properties
- CDF is a non-decreasing.
- The minimum of CDF is 0 when x = – infinity: Fx(- inf) = 0.
- The maximum of CDF is 1 when x = infinity: Fx(inf) = 1
- P [a <= x <= b] = FX(b) – FX(a)
Example
Consider the pdf function given in the above example and find the CDF for ½ <= x <= 3/2.
Answer:
| Programming Online Courses and Certification | Python Online Courses and Certifications |
| Data Science Online Courses and Certifications | Machine Learning Online Courses and Certifications |
Relation Between PDF and CDF
- The probability distribution function (PDF) gives the probability that a random variable takes on a specific value.
- The cumulative distribution function (CDF) gives the probability that a random variable is less than or equal to a certain value.
- The CDF is the integral of the PDF, which means the CDF accumulates the probabilities from the PDF up to a certain point.
- The PDF and CDF are related such that the CDF can be obtained by integrating the PDF, and the PDF can be obtained by differentiating the CDF.
- The CDF provides a complete picture of the probabilities associated with a random variable, while the PDF focuses on the probability density at specific points.
What are the key differences between PDF and CDF?
- The probability distribution function (PDF) gives the probability that a random variable takes on a specific value, while the cumulative distribution function (CDF) gives the probability that a random variable is less than or equal to a certain value.
- The PDF provides the probability density at specific points, while the CDF accumulates the probabilities up to a certain point.
- The CDF is always non-decreasing, as it represents the accumulation of probabilities, whereas the PDF does not have this restriction.
- The CDF ranges from 0 to 1, while the PDF can take any non-negative value.
- The CDF can be obtained by integrating the PDF, and the PDF can be obtained by differentiating the CDF.



Conclusion
In this article, we have discussed the probability density function (PDF) and cumulative density function (CDF), their properties and the difference between CDF and PDF with the help of examples.
PDF (or Probability Density Function) is a function that describes the probability of a continuous random variable. The PDF function’s curve looks like a bell-shaped curve, taking the value between the given intervals. In contrast, CDF or Cumulative Distribution Function is a probability that a random variable takes on a value less than or equal to X. The CDF can be defined. for both the random variables: continuous and discrete random variables.
Hope you will like the article.
Keep Learning!!
Keep Sharing!!
Also Read






FAQs on Difference Between
What is PDF?
PDF (or Probability Density Function) is a function that describes the probability of a continuous random variable. The PDF function's curve looks like a bell-shaped curve, and it takes the value between the given intervals.
What is CDF?
CDF (or Cumulative Distribution Function) is a probability that a random variable takes on a value less than or equal to X. The CDF can be defined. for both the random variables: continuous and discrete random variables.
What is the difference between PDF and CDF?
A PDF, or Probability Density Function, shows the likelihood of a continuous random variable assuming specific values. In contrast, a CDF, or Cumulative Distribution Function, represents the probability that the variable is less than or equal to a particular value. The PDF is used more for continuous variables, while the CDF can be applied to both continuous and discrete variables.
When to use PDF and CDF?
PDF is mainly used in statistical analysis and modeling to describe the distribution of data, whereas CDF are commonly used in statistical analysis and modeling to calculate probabilities and percentiles.
Can a PDF convert to a CDF?
Yes, PDF can be converted to a CDF by integrating the PDF over its entire domain. The resulting function will be the CDF of the random variable and vice versa.
How do PDF and CDF function for discrete random variables?
For discrete random variables, the PDF (in this case, more accurately referred to as a Probability Mass Function or PMF) outlines the probabilities for each specific value. The CDF accumulates these probabilities, showing the cumulative probability for values up to and including a specific point.
Can you calculate probabilities using both PDF and CDF?
Yes, both can be used to calculate probabilities, but in different ways. For continuous random variables, the PDF can find cumulative probabilities over a range, whereas the CDF gives the cumulative probability up to a specific value.

Vikram has a Postgraduate degree in Applied Mathematics, with a keen interest in Data Science and Machine Learning. He has experience of 2+ years in content creation in Mathematics, Statistics, Data Science, and Mac... Read Full Bio