What is a Feasible Solution in LPP?

Imagine you're building a treehouse! You need the right materials (wood, nails) and to follow the instructions (blueprint). A feasible solution is kind of like that in math. It's an answer to a problem that follows all the rules. This article will explain what feasible solutions are and why they're important. We'll use fun examples to show how finding a feasible solution is like following a recipe or playing a game with specific rules. So, get ready to explore the world of possible answers and see how they help us solve problems!

In the previous articles, we have discussed Linear Programming Problems and, its special case Transportation Problems. Now we will learn how to solve the linear programming problem, and for that, in this article, we will discuss one of the key concepts used to solve the LPP, i.e., ‘feasible solution’.

This article is all about a feasible solution, a basic feasible solution, and the different methods to find the feasible solution in LPP.

So, let’s start with the formal definition of a Feasible Solution.

Must Check: Top Math Courses for Data Science

Must Check: Top Data Science Online Courses and Certifications

What is a Feasible Solution?

Feasible solutions are the fundamental concepts used in the Linear Programming Problem. It is defined as “the solution that satisfies all the constraints of a problem“.

Confused!!

Don’t worry.

Let me explain to you with the help of an example.

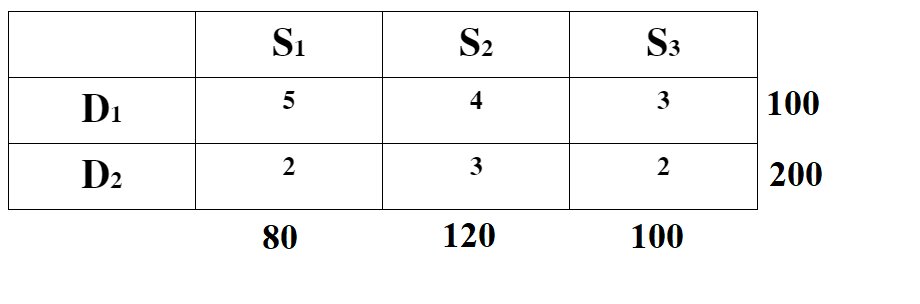
Example: A company has two warehouses (W₁ and W₂) with a production capacity of 100 and 200 units per week of a product, respectively. The company needs to ship all these products to its three stores (S1, S2, and S3), which require 80, 120, and 100 units, respectively. The transportation cost per unit between the warehouse and the store is given in the table below.

Now, let’s formulate the above Transportation Problem to minimize the total transportation cost.

Model Formulation

Let x_ij = Number of the product to be transported from a warehouse i (i = 1, 2) to the stores j (j = 1, 2, 3)

The mathematical formulation of the above transportation problem is as follows:

Min Z (total transportation cost) = 5x₁₁ + 4x₁₂ + 3x₁₃ + 2x₂₁ + 3x₂₂ + 2x₂₃

Subject to the constraints:

Supply Constraints

x₁₁ + x₁₂ + x₁₃ = 100

x₂₁ + x₂₂ + x₂₃ = 200

Demand Constraints

x₁₁ + x₂₁ = 80

x₁₂ + x₂₂ = 120

x₁₃ + x₂₃ = 100

and

x_ij >= 0, for i = 1, 2 and j = 1, 2, and 3

Note:

1. The above formulation can be represented as:

Min Z = ΣΣ c_ij * x_ij, i = 1, 2, and j = 1, 2, 3

Subject to the constraints:

Σ x_ij = a_i (supply constraints)

Σ x_ij = b_j (Demand Constraints)

2. In the above Linear Programming Problem, there are 

Number of Decision Variable (x₁₁, x₁₂, x₁₃, x₂₁, x₂₂, and x₂₃) = m * n = 2 * 3 = 6

Number of Constraints (= Number of Supply Constraint + Number of Demand Constraint) = m + n = 2 + 3 = 5

where,

m = Number of Rows

n = Number of Columns

Existence of Feasible Solution

A necessary and sufficient condition for a feasible solution to the LPP is:
Total Supply = Total Demand, i.e.,

Σ a_i = Σ b_j, for i = 1, 2 and j = 1, 2, 3

In simple terms, the feasible solution for any given linear programming problem exists if and only if Total Supply = Total Demand.

Here, in the above problem:

Total Supply = 80 + 120 + 100 = 300

Total Demand = 100 + 200 = 300

=> Total Demand = Total Supply = 300

Hence, the above transportation problem has a feasible solution.

Note:

• In the above problem, there are m + n (2 + 3 = 5) constraints and m * n (2 * 3 = 6) variables. Since all the constraints are equations.
  • i.e., we have 6 variables and 5 equations.
• Therefore, we have 5 independent variables and one dependent variable. The value of the one dependent variable can be derived from the remaining 5 constraints.
• In any linear programming problem, there must be exactly (m + n – 1) non-negative basic variables satisfying the condition of a feasible solution.

• When the Total Supply = Total Demand, the problem is called a Balanced Transportation Problem, otherwise it is called Unbalanced Transportation Problem.
• When the number of Decision Variable is less than the required number (m + n – 1), then the solution is said to be a degenerate solution, otherwise a non-degenerate solution.
• Cells in the transportation problem having positive allocations x_ij > = 0 are called occupied cells, otherwise known as non-occupied cells.

Methods to Find the Feasible Solution

There are different methods to find the feasible solution for any given Linear programming Problem (LPP)

1. Graphical Method
2. Simplex Method
3. Dual Simplex Method
4. Interior Method
5. Sensitivity Analysis

Methods to Find the Feasible Solution to Transportation Problem

1. North-West Corner Method
2. Least Cost Method
3. Vogel’s Approximation Method
4. MODI Method (Modified Distribution Method)

Conclusion

The feasible solution to a transportation problem is defined as a solution that satisfies all the constraints of a problem.

In this article, we have briefly explained feasible solutions, their existence, and methods for finding them. We hope you will like the article.

Keep Learning!!

Keep Sharing!!