Handwritten Digit Recognition with 98% Accuracy

In this Tensorflow tutorial, you will learn how to train a multi layer perceptron on MNIST dataset for Handwritten Digit Recognition.

Almost everyone around as have different handwriting. Reading it might be easy for you, but when it comes to extract information out of it digitally might be bit tricky. Well not anymore, in this tutorial I will guide you with how you can use Tensorflow to train your machine with Handwritten Digit Recognition dataset with 98% accuracy. You can later modify it train on your own custom dataset.

Problem Statement: Handwritten Digit Recognition

MNIST (“Modified National Institute of Standards and Technology”) is considered an unofficial computer vision “hello-world” dataset. This is a collection of thousands of handwritten pictures used to train classification models using Machine Learning techniques.

As a part of this problem statement, we will train a multi layer perceptron using Tensorflow -v2 to recognize the handwritten digits.

Things to be covered in this blog:

• Install the latest Tensorflow library
• Prepare the dataset for the model
• Develop Single Layer Perceptron model for classifying the handwritten digits
• Plot the change in accuracy per epochs
• Evaluate the model on the testing data
• Analyze the model summary
• Add hidden layer to the model to make it Multi-Layer Perceptron
• Add Dropout to prevent overfitting and check its effect on accuracy
• Increasing the number of Hidden Layer neuron and check its effect on accuracy
• Use different optimizers and check its effect on accuracy
• Increase the hidden layers and check its effect on accuracy
• Manipulate the batch_size and epochs and check its effect on accuracy

MNIST Dataset Description

The MNIST Handwritten Digit Recognition Dataset contains 60,000 training and 10,000 testing labelled handwritten digit pictures.

Each picture is 28 pixels in height and 28 pixels wide, for a total of 784 (28×28) pixels. Each pixel has a single pixel value associated with it. It indicates how bright or dark that pixel is (larger numbers indicates darker pixel). This pixel value is an integer ranging from 0 to 255.

Install the latest Tensorflow 2.x version

For this tutorial blog we will be pip installing the latest version of Tensorflow:

Output: 2.8.0

Each time you will execute the above code it will install the latest version of Tensorflow for you. Currently for me its 2.8.0. We are importing keras from the Tensorflow library and checking its version to verify if our installation was successful. You will get an error as tensorflow not found on unsuccessful installation.

NOTE: Keras is now a part of Tensorflow 2.x

Preparing the Handwritten Digit Recognition dataset

Let’s fetch and explore MNIST dataset from the Keras library

This block of code will load the images of handwritten digits from mnist dataset and randomly split the it as X_train, Y_train (to separate the features and label of training data) and X_test, Y_test (features and label of testing data). These split datasets will be used to train and test our model.

Let’s check the number of entries in our dataset. For this we will be printing the shape of X_train and X_test.

Output:

(60000, 28, 28)

(10000, 28, 28)

From the above output we can see that we have 60000 entries (images) as part of train data with 28×28 pixel values and 10000 entries as a part of test of data of same size. You can check the individual pixels of any of the image, eg: X_train[0].

Let’s preprocess our data for further usage. We will reshape the dataset from 28×28 to 784 and convert it into float32 datatype for training our neural network.

• Reshape the data
• Change the datatype to float32
• Normalize the dataset
• Perform One-Hot Encoding on the labels

Output:

60000 train samples

10000 test samples

The output tells the number of records within the train and test data.

Now that we have prepared our data. Next we will be using this data to build our model.

Building the Handwritten Digit Recognition Models

Preparing the 1st Model: Single layer Perceptron

This model is the most basic sequential model with 0 hidden layers in it.

Adding the model layer

We will be building the simplest model defined in the Sequential class as a linear stack of Layers

Syntax:

For Example:

NOTE:

• Here the model will take input array of shape (*, 784) and outputs array of shape (*, 10).
• Dense layer is a fully connected layer and the most common type of layer used on multi layer perceptron models

Adding Activation Function to the model layer

Activation function is defined in the dense layer of the model and is used to squeeze the value within a particular range. In simple term it is a function which is used to convert the input signal of a node to an output signal. tf.keras comes with the following predefined activation functions to choose from:

• softmax
• sigmoid
• tanh
• relu

It is defined as below, example:

Lets stich them together

Code:

In the above code we are importing the sequential keras model with 0 hidden layers. We have defined the output layer as 10. This is our dense layer. 10 is chosen as we have numbers from 0 to 9 to be classified in the dataset. shape. Total number of neurons in the input layer is 784. The activation function chosen in the dense layer is softmax. We will learn more about the softmax function in detail in our next blog. In simple terms, the model will have 784 input neurons to give the output between 0-9 numbers.

Compiling the model

Next step is to compile the model. For compiling we need to define three parameters: optimizer, loss, and metrics.

Syntax:

model.compile (optimizer=…, loss=…, metrics = …)

1. Optimizer: While training a deep learning model, we need to alter the weights of each epoch and minimize the loss function. An optimizer is a function or algorithm that adjusts the neural network’s properties such as weights and learning rate. As a result, it helps to reduce total loss and enhance accuracy of your model.

Some of the popular Gradient Descent Optimizers are:

• SGD: Stochastic gradient descent, to reduce the computation cost of gradient
• RMSprop: Adaptive learning rate optimization method which utilizes the magnitude of recent gradients to normalize the gradients
• Adam: Adaptive Moment Estimation (Adam) leverages the power of adaptive learning rates methods to find individual learning rates for each parameter

For Example:

2. Loss: Loss functions are a measure of how well your model predicts the predicted outcome.
Some of the popular Model Loss Function are:

• mse : for mean squared error
• binary_crossentropy:for binary logarithmic loss (logloss)
• categorical_crossentropy: for multi class logarithmic loss (logloss)

For example:

Let’s put them together in the code:

Training the model

Model will be now trained on the on the training data. For this we will be defining the epochs, batchsize, and validation size

• epoch: Number of times that the model will run through the training dataset
• batch_size: Number of training instances to be shown to the model before a weight is updated
• validation_split: Defines the fraction of data to be used for validation purpose

Syntax:

Let’s put it together in the code,

Output:

Epoch 1/70

750/750 [==============================] – 1s 2ms/step – loss: 1.0832 – accuracy: 0.7526 – val_loss: 0.6560 – val_accuracy: 0.8587

Epoch 2/70

750/750 [==============================] – 1s 2ms/step – loss: 0.6081 – accuracy: 0.8562 – val_loss: 0.5083 – val_accuracy: 0.8778

Epoch 3/70

750/750 [==============================] – 1s 2ms/step – loss: 0.5130 – accuracy: 0.8701 – val_loss: 0.4506 – val_accuracy: 0.8865

Epoch 4/70

750/750 [==============================] – 1s 2ms/step – loss: 0.4667 – accuracy: 0.8784 – val_loss: 0.4181 – val_accuracy: 0.8929

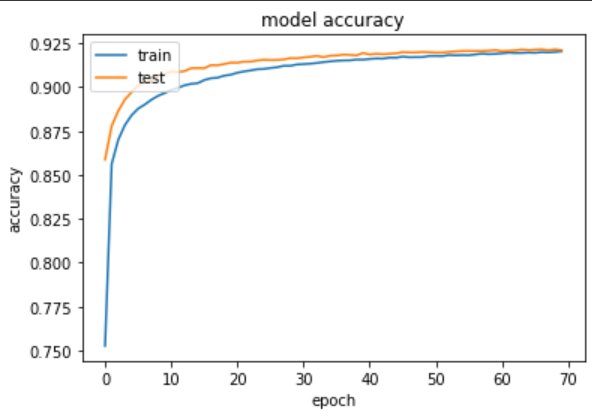
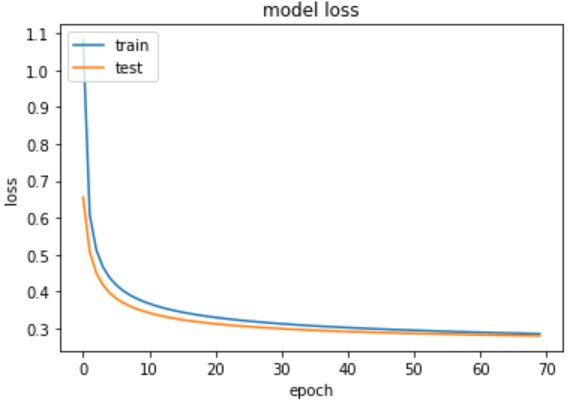
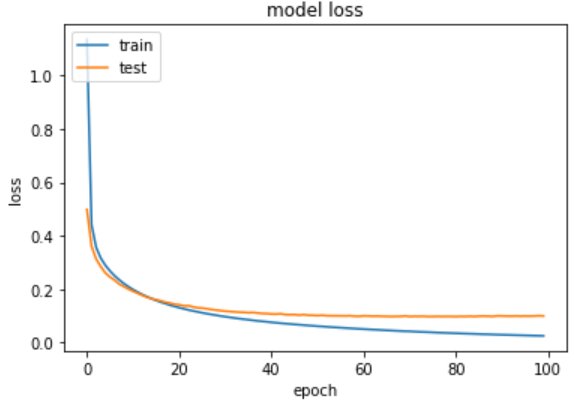
From the above output you can see that with each epoch the loss is reduced and the val_accuracy is being improved.

Plot the change in accuracy and loss per epochs

You can plot a curve to check the variation of accuracy and loss as the number of epochs increases. For this you can use, matplotlib to plot the curve.

Output:

Evaluating the Handwritten Digit Recognition Model on Test Data

We will now test the accuracy of the model on the testing dataset.

Output:

313/313 [==============================] – 0s 1ms/step – loss: 0.2827 – accuracy: 0.9210

Test accuracy: 0.9210000038146973

Finally you can check the configuration of the model using get_config()

Output:

{‘build_input_shape’: TensorShape([None, 784]),
‘layers’: [{‘class_name’: ‘Dense’,
‘config’: {‘activation’: ‘softmax’,
‘activity_regularizer’: None,
‘batch_input_shape’: (None, 784),
‘bias_constraint’: None,
‘bias_initializer’: {‘class_name’: ‘Zeros’, ‘config’: {}},
‘bias_regularizer’: None,
‘dtype’: ‘float32’,
‘kernel_constraint’: None,
‘kernel_initializer’: {‘class_name’: ‘GlorotUniform’,
‘config’: {‘seed’: None}},
‘kernel_regularizer’: None,
‘name’: ‘dense_layer’,
‘trainable’: True,
‘units’: 10,
‘use_bias’: True}}],
‘name’: ‘sequential_8’}

Next step is to improve the base model we just created. This base model is a single layer perceptron with zero hidden layers. Let’s add some hidden layers to our model to check if it improves the accuracy.

Improved Model 2: Adding Hidden Layer – Multi Layer Perceptron

In the model we will add a hidden layer and 3 dense layer. The hidden layer consists of 64 neurons. The new dense_layer_2 has 64 neurons and relu activation layer. Let’s experiment by increasing the number of epochs to 100 in this model.

Output:

Epoch 1/100

750/750 [==============================] – 2s 2ms/step – loss: 1.1360 – accuracy: 0.7017 – val_loss: 0.4982 – val_accuracy: 0.8706

Epoch 2/100

750/750 [==============================] – 2s 2ms/step – loss: 0.4416 – accuracy: 0.8785 – val_loss: 0.3600 – val_accuracy: 0.8966

Epoch 3/100

750/750 [==============================] – 2s 2ms/step – loss: 0.3561 – accuracy: 0.8987 – val_loss: 0.3126 – val_accuracy: 0.9104

Epoch 4/100

750/750 [==============================] – 2s 2ms/step – loss: 0.3161 – accuracy: 0.9096 – val_loss: 0.2842 – val_accuracy: 0.9181

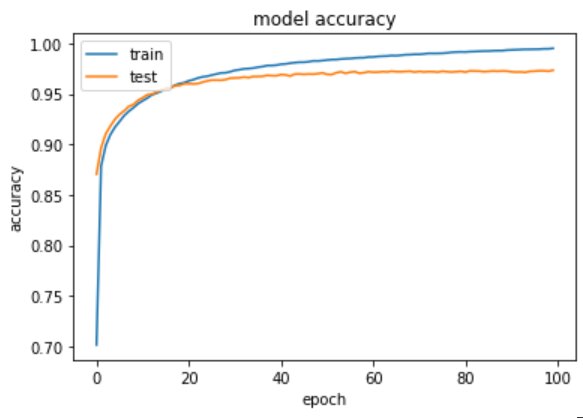
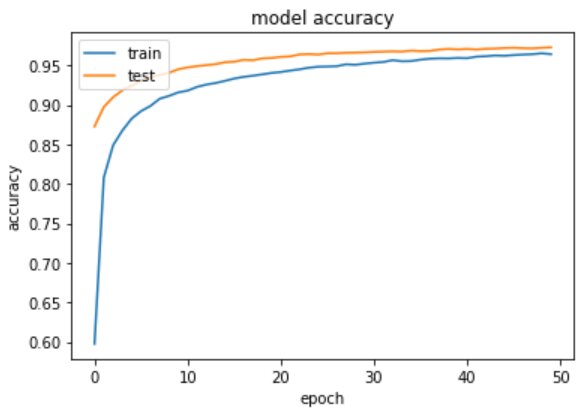
As compared to the previous model the loss is further reduced and the val_accuracy is improved.

Plot the change in accuracy and loss per epochs

Plotting the change in metrices per epochs using matplotlib

Model 2 – Evaluate the Handwritten Digit Recognition Model on Test Data

Output:

313/313 [==============================] – 0s 1ms/step – loss: 0.0935 – accuracy: 0.9737

Test accuracy: 0.9736999869346619

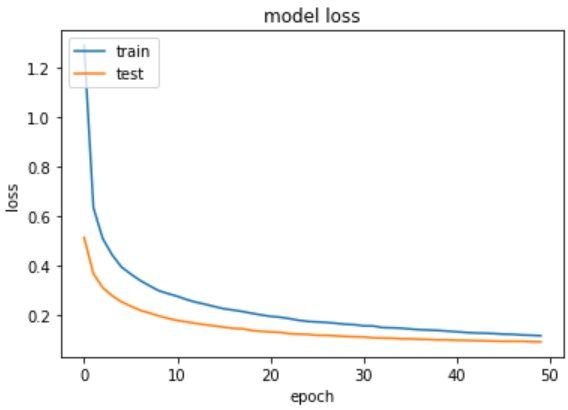
The second model is giving an output of 97%. Further we can improve the model by adding a dropout to avoid overfitting.

Improved Model 3 – Adding Dropout to Avoid Overfitting

In this new improved model we will be adding an dropout of 0.3 to avoid the overfitting.

Output:

Epoch 1/50

750/750 [==============================] – 2s 3ms/step – loss: 1.2920 – accuracy: 0.5974 – val_loss: 0.5148 – val_accuracy: 0.8725

Epoch 2/50

750/750 [==============================] – 2s 3ms/step – loss: 0.6353 – accuracy: 0.8080 – val_loss: 0.3688 – val_accuracy: 0.8972

Epoch 3/50

750/750 [==============================] – 2s 3ms/step – loss: 0.5108 – accuracy: 0.8489 – val_loss: 0.3122 – val_accuracy: 0.9096

Epoch 4/50

750/750 [==============================] – 2s 3ms/step – loss: 0.4453 – accuracy: 0.8675 – val_loss: 0.2800 – val_accuracy: 0.9183

Model 3 – Plot the change in metrices per epochs

Model 3 – Evaluate the Handwritten Digit Recognition Model on Test Data

Output:

313/313 [==============================] – 0s 1ms/step – loss: 0.0870 – accuracy: 0.9728

Test accuracy: 0.9728000164031982

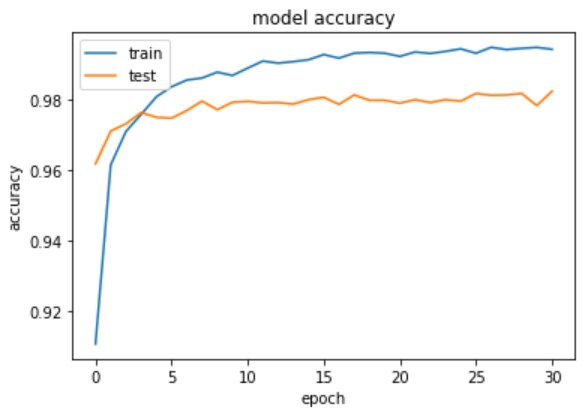
Improved Model 4: Increasing the number of Hidden Layer neuron

Output:

Epoch 1/31

375/375 [==============================] – 6s 16ms/step – loss: 0.2993 – accuracy: 0.9108 – val_loss: 0.1264 – val_accuracy: 0.9619

Epoch 2/31

375/375 [==============================] – 6s 15ms/step – loss: 0.1253 – accuracy: 0.9616 – val_loss: 0.0939 – val_accuracy: 0.9712

Epoch 3/31

375/375 [==============================] – 6s 15ms/step – loss: 0.0913 – accuracy: 0.9711 – val_loss: 0.0869 – val_accuracy: 0.9732

Epoch 4/31

375/375 [==============================] – 6s 15ms/step – loss: 0.0741 – accuracy: 0.9759 – val_loss: 0.0789 – val_accuracy: 0.9764

Model 4 – Plot the change in metrices per epochs

Output:

Model 4 – Evaluate the Handwritten Digit Recognition Model on Test Data

Output:

313/313 [==============================] – 1s 3ms/step – loss: 0.0831 – accuracy: 0.9824

Test accuracy: 0.9824000000953674

Final accuracy of our trained model comes to be 98%.

Conclusion

I hope I was able to explain how to train a multilayer perceptron step by step. Our final model accuracy is 98%. In our next blog I will show you how you can use Convolutional Neural Network to train your model built on a custom dataset. For more detail on Tensorflow you can check out these Top Tensorflow courses and certifications in the industry.