Introduction to Inferential Statistics

Introduction:

The branch of mathematics that deals with the collection, analysis, prediction, and presentation of numerical data is known as Statistics.

Statistics is mainly categorized into two types:

• Descriptive Statistics
• Inferential Statistics

Table of Content:

• What are Population and Sample?
• What is Inferential Statistics?
  • Probability
  • Probability Distributions
  • Confidence Interval
  • Hypothesis Testing
  • p-value
  • z-test and t-test
  • Chi-square test
  • ANOVA test

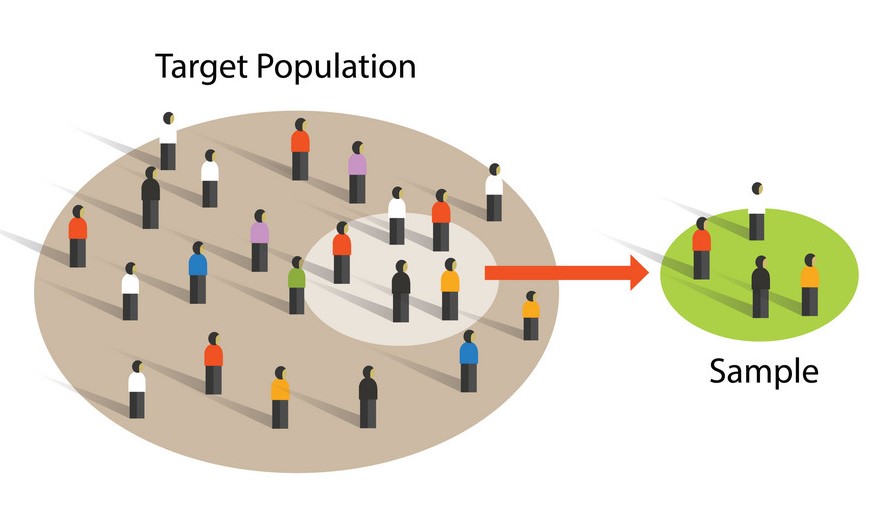
What are Population and Sample?

• The population is the set of all the data points that you draw to make an experiment.
• The sample is a subset of the population that is used to make a conclusion about the population.

Characteristics of Sample:

• Randomly Selected
• Unbiased
• Represents all types of data points from the population

What is Inferential Statistics?

Inferential statistics is a tool that makes inferences (conclusions) about the population data using the sample set.

Example: Average number of hours school students play video games

There are two ways to collect the data

1. Visit all the schools of your district
2. Visit all the schools in the country

The second method is expensive, time-taking while collecting the information of your district need less effort, money and time.

It may be possible that the average time spent on video games in your district is:

• quite low or
• extremely high,

due to the other facilities available in your district and elsewhere in the other parts of the country.

In inferential statistics, we will discuss probability, probability distribution, hypothesis testing, t-test, chi-square test and ANOVA test.

Let’s start with the probability

Probability:

Probability is defined as the likeliness of something to occur or happen.

Example: Getting head on tossing a coin

Now, let’s discuss some basics concepts of Probability:

• Random Experiment: 

Random experiment is a process for which outcome can’t be predicted with certainty

Or 

A random experiment is a process by which we observe something uncertain.

Example: Rolling a dice

• Outcome: 

Outcome is a result of a random experiment.

Example: In rolling dice, there are 6 possible outcomes 1, 2, 3, 4, 5, 6

• Sample Space: 

Set of all possible outcomes.

Example: Sample space of rolling dice: {1, 2, 3, 4, 5, 6}

• Trials:

When a random experiment is repeated, then each random experiment is known as Trials.

Example: Flipping of a coin

• Event:

A subset of the sample space

Example: Set of even {2, 4, 6} or odd {1, 3, 5} outcomes on rolling dice

• Random Variable: 

A real valued function defined on the sample space is called Random Variable.

Example: Sum of outcomes on rolling two dice

Probability Distributions:

A Probability Distribution of a random variable is a list of all possible outcomes with corresponding probability values.

Example:

Types of Probability Distributions:

• Uniform Distribution
• Bernoulli Distribution
• Binomial Distribution
• Poisson Distribution
• Normal Distribution

To know more about probability distributions read the article on Probability Distributions.

Confidence Interval:

Confidence interval is the range of values that is likely to include a population value with a certain degree of confidence.

It is expressed in %, where a population mean lies between the range of confidence intervals.

Example: 95% confidence interval for the population mean height of Males (150 cm, 180 cm) indicates that we are 95% confident that the mean height of the male lies between 150 cm and 180 cm.    

Hypothesis Testing:

A Hypothesis is an assumption or an idea that is proposed for the sake of argument so that it can be tested to see if it might be true.

Example: COVID Vaccine: Covaxin might work for COVID-19 or not

Hypothesis testing is a statistical method to validate your assumptions whether they are True or False or they have some significance.

Types of Hypothesis:

A hypothesis is classified into two types:

• Null Hypothesis

• • • A statement about a population parameter
    • States that the population parameter ( mean, variance etc.) is equal to the assumed value
    • Represented by H0.

• Alternate Hypothesis

  • • A statement that directly contradicts the Null Hypothesis
    • states that the population parameter is smaller, greater or different from our assumption
    • Represented by Ha.

Example:

We want to test whether the mean score of students in statistics is different from 35 (out of 50). The null and alternative hypotheses are

H0: μ = 2.0

Ha: μ ≠ 2.0

p-value:

P-value is a numeric value use to reject or accept the null hypothesis.

The most common used p-value is 0.05.

• If p ≤ 0.05, reject the null hypothesis.
• If p > 0.05, accept the null hypothesis

z-test and t-test:

z-test	t-test
Hypothesis test used when the sample size is greater than 30	Hypothesis test used when the sample size is less than 30
Population variance and standard deviation are known	Population variance and standard deviation are not known
All the elements of the sample are independent	All the elements of sample need not be independent

Chi-squared test: 

Chi-square test used for Hypothesis testing of the categorical data to compare the observed result with the expected result.

Test is used for sample size of less than 50.

ANOVA Test:

Analysis of variance(ANOVA) is used to check whether the means of two or more groups are significantly different from each other.

It checks the impact of one or more factors by comparing the means of different samples.

Conclusion:

In this article, we cover all the topics of inferential statistics starting with the probability, distribution, hypothesis testing, p-value, z-test, t-test, and chi-squared test. Hope you will enjoy the article.

————————————————————————————————————–
If you have recently completed a professional course/certification, click here to submit a review.

Frequently Ask Question (FAQ)

Ques 1. What are Population and Sample?

Ans 1.

• The population is the set of all the data points that you draw to make an experiment.
• The sample is a subset of the population that is used to make a conclusion about the population.

Ques 2: What is Inferential Statistics?

Ans 2. Inferential statistics is a tool that makes inferences (conclusions) about the population data using the sample set.

Example: Average number of hours school students play video games

Ques 3. What is Hypothesis Testing?

Ans 3. A Hypothesis is an assumption or an idea that is proposed for the sake of argument so that it can be tested to see if it might be true.

Example: COVID Vaccine: Covaxin might work for COVID-19 or not.

Top Trending Articles in Statistics:

Skewness In Statistics | Statistics Interview Question | Basics Of Statistics | Measure Of Central Tendency | Probability Distribution | Inferential Statistics | Measure Of Dispersion | Introduction To Probability | Bayes Theorem | P-Value | Z-Test | T-Test | Chi-Square Test | Outliers In Python | Sampling and Resampling | Regression Analysis In Machine Learning | Gradient Descent | Normal Distribution | Poisson Distribution | Binomial Distribution | Covariance And Correlation | Conditional Probability | Central Limit Theorem