Merge Sort Algorithm (With Code)
In programming, sorting data is as crucial as organizing a messy library. Imagine you have a vast library with books scattered everywhere, and your job is to arrange them. It might seem like a big task, right? That's where sorting algorithms come in – they're like the librarians of the digital world.
Among these sorting algorithms, Merge Sort is a standout. Think of it as a powerful tool. Imagine a digital library with thousands of e-books all mixed up. People are having a hard time finding the books they want to read. That's where Merge Sort comes to help. It acts like an organized librarian.
So, how does Merge Sort work? It's like this librarian divides the e-books into smaller groups, sorts each group, and then puts them all back together neatly. That's the essence of Merge Sort – it takes a big problem, breaks it down into smaller parts, and then combines them to create a perfectly sorted collection.
Table of Contents
- How Does Merge Sort Work?
- Algorithm
- Initial Array
- Dry Run Table
- Pseudo Code
- Time Complexity
- Space Complexity
- Real-World Problem
- Advantages and Disadvantages of Merge Sort in C
How Does Merge Sort Work?
Merge Sort is like a wise sage who knows that the best way to tackle a problem is by breaking it down. It is a recursive method, which means it calls itself to solve smaller parts of a larger problem. Imagine splitting a deck of cards into halves, over and over, until you have piles so small they're already sorted.
Illustration:
Here's a simple way to visualize Merge Sort:
- Divide: Split your array of data in half, again and again, until each piece can't be divided further (you'll end up with arrays of just one element).
- Conquer: Now, with each piece being sorted (since it's just one element), you start combining them.
- Merge: As you combine these pieces, you sort them along the way. Think of merging two small stacks of cards where each stack is already in order.
This process continues until all the small, sorted pieces are merged back into a single, sorted array.

Best-suited Data Structures and Algorithms courses for you
Learn Data Structures and Algorithms with these high-rated online courses
Algorithm
Step 1: Create two pointers, one for each sorted half.
Step 2: Initialize an empty temporary array to hold the merged result.
Step 3: Compare the elements at the pointers of the two halves:
Copy the smaller element into the temporary array.
Move the pointer of the sublist with the smaller element forward.
Step 4: Repeat step 3 until one of the sublists is empty.
Step 5: Copy the remaining elements from the non-empty sublist to the temporary array.
Step 6: Copy the elements back from the temporary array to the original list.

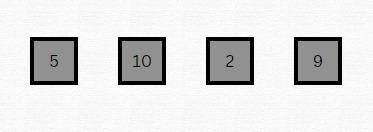
Initial Array
We start with an unsorted array of numbers. The purpose of Merge Sort will be to sort this array in ascending order.
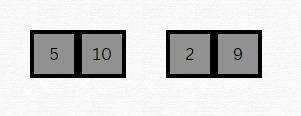
Step 1: Dividing the Array
Merge Sort begins with a divide-and-conquer approach. The array is divided into two halves, which is represented in the second image where the array [5, 10, 2, 9] is split into two subarrays: [5, 10] and [2, 9]. This division continues recursively until we cannot divide the arrays any further, typically when we reach arrays of single elements.
Step 2: Sorting Subarrays
Once we have our subarrays, each is sorted individually. In the case of single-element arrays, they are already sorted by definition. So, our subarrays [5, 10] and [2, 9] are considered sorted because they are composed of single elements after further division.
Step 3: Merging Subarrays
After sorting the subarrays, Merge Sort enters the conquer phase, which involves merging the sorted subarrays. This is where we combine our subarrays into larger, sorted arrays. We compare the elements at the beginning of each subarray and place the smaller one into the new array first.
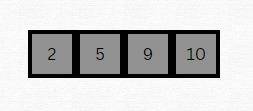
Step 4: Final Merging
The last image represents the final merge where two sorted halves of the original array are combined to form the final sorted array. If there were more elements, the merge process would continue until all subarrays are merged into a single sorted array.
In each merging step, the algorithm follows the same principle: comparing the front elements of each subarray and picking the smaller one to place into the new, sorted subarray. This process is repeated until all elements are sorted and merged.

Dry Run Table
| Step |
Left Subarray |
Right Subarray |
Merged Array |
|
|
[5, 10, 2, 9] |
|
|
| 1 |
[5, 10] |
[2, 9] |
|
| 2 |
[5] |
[10] |
[5, 10] |
| 3 |
[2] |
[9] |
[2, 9] |
| 4 |
|
|
[2, 5, 9, 10] |
To summarize, Merge Sort divides the array into smaller subarrays until each subarray is trivially sorted (containing a single element), and then merges those subarrays back together in a way that results in a sorted array. The key operation in this algorithm is the merge step, which takes two sorted arrays and merges them into a single sorted array. This process, applied recursively, results in the entire array being sorted.
Pseudo Code
Before diving into C code, let's sketch a roadmap with pseudo-code:
function mergeSort(array) if length of array <= 1 return array middle = length of array / 2 leftArray = mergeSort(first half of array) rightArray = mergeSort(second half of array) return merge(leftArray, rightArray)
Code (C):
Now, let's translate our pseudo-code into C:
#include <stdio.h>
// Function to merge two sorted subarraysvoid merge(int arr[], int l, int m, int r) { // Calculate sizes of two subarrays to be merged int n1 = m - l + 1; int n2 = r - m;
// Create temporary arrays to hold the subarrays int L[n1], R[n2];
// Copy data to temporary arrays for (int i = 0; i < n1; i++) L[i] = arr[l + i]; for (int j = 0; j < n2; j++) R[j] = arr[m + 1 + j];
// Merge the temporary arrays back into arr[l..r] int i = 0, j = 0, k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; }
// Copy remaining elements of L[], if any while (i < n1) { arr[k] = L[i]; i++; k++; }
// Copy remaining elements of R[], if any while (j < n2) { arr[k] = R[j]; j++; k++; }}
// Recursive function to perform merge sortvoid mergeSort(int arr[], int l, int r) { // Base case: If there is only one element, do nothing if (l < r) { // Find the middle point to divide the array into two halves int m = l + (r - l) / 2;
// Recursively sort the left and right halves mergeSort(arr, l, m); mergeSort(arr, m + 1, r);
// Merge the sorted halves merge(arr, l, m, r); }}
int main() { int arr[] = {5, 10, 2, 9}; int n = sizeof(arr) / sizeof(arr[0]);
printf("Unsorted array: \n"); for (int i = 0; i < n; i++) printf("%d ", arr[i]);
mergeSort(arr, 0, n - 1);
printf("\nSorted array: \n"); for (int i = 0; i < n; i++) printf("%d ", arr[i]);
return 0;}
Output:
Unsorted array:
5 10 2 9
Sorted array:
2 5 9 10
Time Complexity
The time complexity of an algorithm quantifies the amount of time it takes to run as a function of the length of the input. For Merge Sort, this is particularly interesting.
- Divide Step: This step divides the array into halves, and it takes constant time, O(1), for each level of recursion.
- Conquer Step: Here, we recursively solve two subproblems, each of size roughly half of the original problem. This gives us a time complexity of 2T(n/2) for this step, where T(n) is the time complexity of Merge Sort.
- Combine Step (Merging): The merging of two sorted halves can be done in O(n) time.
Merge Sort follows the Master Theorem for dividing recursive algorithms. The Master Theorem tells us that the time complexity of Merge Sort is O(n log n), where 'n' is the number of elements in the array. This O(n log n) complexity holds true for the worst, average, and best cases, which is one of the strengths of Merge Sort.

Space Complexity
Space complexity measures the total amount of memory that an algorithm or operation needs to run according to its input size.
- Auxiliary Space for Merging: Merge Sort is not an in-place sorting algorithm. It requires additional space to merge two sorted arrays. This additional space is proportional to the size of the input array, i.e., O(n).
- Recursion Stack Space: Merge Sort is a recursive algorithm, and it requires additional space on the stack. The depth of the recursion tree is log n (since the array is divided into half in each step). Therefore, the space complexity due to the recursion stack is O(log n).
Combining these two, the overall space complexity of Merge Sort is O(n) + O(log n), which simplifies to O(n), as the O(n) term dominates the O(log n) term. Thus, the space complexity of Merge Sort is O(n).
In summary, Merge Sort has a time complexity of O(n log n) and a space complexity of O(n). This efficiency in time comes at the cost of space, as Merge Sort requires additional memory for its operations.

Real-World Problem
Problem:
Visualize: Imagine a doctor has a list of patients waiting for surgery, each needing the procedure urgently but with varying priority levels based on medical severity. The doctor needs to efficiently schedule the surgeries to prioritize the most critical patients while minimizing wait times for all.
Task:
- Sort the patient list in descending order of priority, ensuring the most critical patients are at the top of the list.
Solution:
Divide: Divide the list of patients into two halves based on their current wait times or other factors affecting urgency.
Conquer: Recursively sort each half using Merge Sort, ensuring proper ordering within each sub-list.
Combine: Merge the two sorted sub-lists into a single, prioritized list, placing the most critical patients at the beginning.
Code in C:
#include <stdio.h>#include <stdlib.h>
// Structure to represent a patient with name and priority leveltypedef struct Patient { char name[50]; int priority;} Patient;
// Function to compare two patients by priority (descending)int comparePatients(const void *a, const void *b) { const Patient *patient1 = (const Patient *)a; const Patient *patient2 = (const Patient *)b; return patient2->priority - patient1->priority;}
// Function to merge two subarrays of patients (descending priority)void merge(Patient patients[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m;
Patient L[n1], R[n2];
for (i = 0; i < n1; i++) { L[i] = patients[l + i]; } for (j = 0; j < n2; j++) { R[j] = patients[m + 1 + j]; }
i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (comparePatients(&L[i], &R[j]) > 0) { patients[k] = L[i]; i++; } else { patients[k] = R[j]; j++; } k++; }
while (i < n1) { patients[k] = L[i]; i++; k++; }
while (j < n2) { patients[k] = R[j]; j++; k++; }}
// Function to perform merge sort on the patient listvoid mergeSortPatients(Patient patients[], int l, int r) { if (l < r) { int m = l + (r - l) / 2; mergeSortPatients(patients, l, m); mergeSortPatients(patients, m + 1, r); merge(patients, l, m, r); }}
int main() { Patient patients[] = { {"John Smith", 5}, {"Jane Doe", 3}, {"Alice Jones", 1}, {"Bob Lee", 4}, {"Mike Brown", 2}, }; int n = sizeof(patients) / sizeof(patients[0]);
printf("Unsorted patient list:\n"); for (int i = 0; i < n; i++) { printf("%s (priority: %d)\n", patients[i].name, patients[i].priority); }
mergeSortPatients(patients, 0, n - 1);
printf("\nSorted patient list (high priority first):\n"); for (int i = 0; i < n; i++) { printf("%s (priority: %d)\n", patients[i].name, patients[i].priority); }
return 0;}
Output:
Unsorted patient list:
John Smith (priority: 5)
Jane Doe (priority: 3)
Alice Jones (priority: 1)
Bob Lee (priority: 4)
Mike Brown (priority: 2)
Sorted patient list (high priority first):
John Smith (priority: 5)
Bob Lee (priority: 4)
Jane Doe (priority: 3)
Mike Brown (priority: 2)
Alice Jones (priority: 1)
Advantages and Disadvantages of Merge Sort in C
Following are the advantages and disadvantages of Merge sort in C:
Advantages of Merge Sort
- Guaranteed worst-case complexity: Merge Sort has a guaranteed O(n log n) time complexity, even in the worst-case scenario. This means the sorting time increases logarithmically with the number of elements, making it efficient for large datasets.
- Stable sorting: Merge Sort preserves the relative order of equal elements. This is useful in situations where the order of identical elements matters, like sorting files by name and creation date.
- Efficient for external sorting: Merge Sort can be efficiently used for external sorting, where the data is too large to fit in memory at once. It breaks down the data into smaller chunks and sorts them on disk before merging them back together.
- Parallelizable: Merge Sort can be easily parallelized by dividing the sorting task across multiple processors or cores, further improving its speed for large datasets.
- No in-place modification: Merge Sort requires additional memory to store the sorted sub-arrays during the merging process. While this can be a disadvantage for small datasets with limited memory, it avoids overwriting the original data, which can be useful for certain applications.
Disadvantages of Merge Sort
- Higher memory usage: As mentioned above, Merge Sort requires additional memory to store the sub-arrays during merging. This can be a disadvantage for small datasets or systems with limited resources.
- Not as efficient for small datasets: For small datasets, Merge Sort's overhead in dividing and merging sub-arrays can make it slower than simpler sorting algorithms like Bubble Sort or Insertion Sort.
- Cache inefficiencies: Merge Sort might suffer from cache inefficiencies due to its access patterns, especially for small datasets. This can be mitigated by careful coding and data organization.
In conclusion, Merge Sort is like a wise, experienced librarian, adept at organizing vast collections of data with precision and efficiency. By understanding and implementing this algorithm in C, you unlock the potential to manage and sort through data with the grace of a well-organized library.
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio