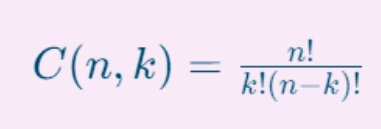Pascal’s Triangle – Definition, Properties, Applications and More
Pascal’s Triangle, named after the French mathematician Blaise Pascal, has roots that stretch much further back in history. The discovery of Pascal’s Triangle wasn’t a single event but rather a gradual development over centuries across different cultures. Let us understand more!
Pascal’s Triangle is a triangular array of numbers. It is a mathematical concept that forms a triangle with numbers, where each number is the sum of the two numbers directly above it. The outer edges of the triangle are always 1. It starts with a single “1” at the top and expands outward with each additional row, making a symmetric, triangular array of binomial coefficients. It looks like this:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
... and so on
Explore Top Pattern Programs in C
The mathematical formula to find the entry in the nth row and kth column (starting from 0) of Pascal’s Triangle is given by the binomial coefficient formula:
It has the following properties:
- Edges are 1s: The numbers on the outer edge of the triangle are all 1s.
- Row Number: If you start numbering rows from 0, the nth number in the nth row is n.
- Binomial Expansion: The coefficients in the binomial expansion of (a+b)n are the numbers in the nth row. For example, for (a+b)4, the coefficients are ‘1 4 6 4 1’, corresponding to a4 + 4a3b + 6a2b2 + 4ab3 + b4.
- Combinatorial Interpretation: The entry in the nth row and kth column (starting counting from 0) of Pascal’s Triangle gives the number of ways to choose k items from n items, also known as “n choose k” or the binomial coefficient.
- Hockey Stick Pattern: If you start from any number and follow a diagonal down and to the right, then turn to follow another diagonal down and to the left, the sum of the numbers in the first diagonal is given by the number where you turn.
- Fibonacci Sequence: If you sum the diagonals’ numbers starting from the 1s on the outer edges, you get the Fibonacci sequence.
- Symmetry: Each row in Pascal’s Triangle is symmetric; the numbers on the left side of the row mirror those on the right.
- Sum of Rows: The sum of rows in the nth row is 2n. For instance, the sum of numbers in a row in 3 is 1+3+3+1 = 8, which is 23.
- Triangles within the Triangle: Pascal’s triangle contains other number triangles like Catalan numbers and triangular numbers.
- Connection to Sierpinski’s Triangle: When you highlight the odd numbers in Pascal’s triangle, a pattern similar to Sierpinski’s Triangle emerges, which is a fractal pattern.
- Hexagonal Numbers: The difference between numbers along diagonals gives the sequence of hexagonal numbers.
- Catalan Numbers: You can find Catalan numbers in Pascal’s triangle by summing entries along shallow diagonals.
- Connection with Lucas Numbers: Similar to the Fibonacci sequence, the Lucas numbers can also be found in Pascal’s triangle but with a slightly different summation rule along the diagonals.
- Power Sums: The sum of the kth entries in the first n rows yields power sums and can be used to find sums of sequences of numbers raised to power k.
- Square Numbers: If you add the numbers in the diagonals parallel to the left-to-right diagonal, the sums are the square numbers.
- Pi Approximation: There are methods to approximate Pi using certain properties of Pascal’s Triangle.
- Multinomial Coefficients: Generalized binomial coefficients called multinomial coefficients can also be represented using Pascal’s Triangle’s extended version.
- Magic 11s: Each row represents the digits of the powers of 11 (up to a point, after which carrying is necessary).
Best-suited Programming courses for you
Learn Programming with these high-rated online courses
Let’s See How We Can Print Pascal’s Triangle Using C++, Python & Java.
Pattern output for 5 rows:
Using C++
Code in C++
#include <iostream>using namespace std;
int main() { int rows, coef = 1, space, i, j; cout << "Enter number of rows: "; cin >> rows;
for(i=0; i<rows; i++) { for(space=1; space <= rows-i; space++) cout << " "; for(j=0; j <= i; j++) { if (j==0 || i==0) coef = 1; else coef = coef*(i-j+1)/j; cout << coef << " "; } cout << endl; } return 0;}
Using Python
Code in Python
def generate_pascals_triangle(rows): triangle = [] # List to hold the rows of Pascal's Triangle
for row_num in range(rows): row = [1] # Every row starts with 1 if triangle: # Check if triangle is not empty (i.e., not the first row) last_row = triangle[-1] # Generate the values for the current row based on the previous row row.extend([last_row[i] + last_row[i + 1] for i in range(len(last_row) - 1)]) row.append(1) # Every row ends with 1 triangle.append(row)
return triangle
def print_pascals_triangle(triangle): # Formatting each row for display row_length = len(' '.join(map(str, triangle[-1]))) # Get the length of the last row when printed for row in triangle: print(' '.join(map(str, row)).center(row_length)) # Center align each row
# Main coderows = int(input("Enter the number of rows: "))triangle = generate_pascals_triangle(rows)print_pascals_triangle(triangle)
Using Java
Code in Java
import java.util.Scanner;
public class PascalTriangle { public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.print("Enter the number of rows: "); int rows = scanner.nextInt();
for(int i = 0; i < rows; i++) { for(int space = 0; space < rows - i; space++) { System.out.print(" "); }
int number = 1; for(int j = 0; j <= i; j++) { System.out.print(number + " "); number = number * (i - j) / (j + 1); } System.out.println(); } scanner.close(); }}
Thus, this is one way of printing Pascal’s triangle using different programming languages.
Applications of Pascal’s Triangle
There are so many applications of this concept, out of which a few are listed below:
- Geometry: It is used to find the number of distinct paths (without backtracking) from one corner to another in a grid.
- Fractal geometry: Pascal’s Triangle modulo 2 is used to create a type of fractal called the Sierpinski Triangle.
- Computer science: It helps in dynamic programming approaches, particularly in problems involving combinations and permutations.
- Computer graphics: It is used in Bezier curves, which are used in various graphic design and drawing applications.
- Finance: Particularly in pricing certain types of financial options, binomial methods that utilize Pascal’s triangle can be used.
Thus, Pascal’s Triangle is an amazing example of how seemingly simple can have deep and varied applications, showcasing the wonder and depth hidden within mathematics. Keep learning, keep exploring!
FAQs
What is Pascal's Triangle?
Pascal's Triangle is a triangular array of numbers where each number is the sum of the two numbers directly above it in the previous row. It starts with a single digit at the top, usually 1, and expands outward with increasing rows, creating a pyramid-like shape. This mathematical concept is used in combinatorics to find combinations and has applications in probability and algebra.
How do you generate Pascal's Triangle?
To generate Pascal's Triangle, start with a 1 at the top. For each subsequent row, place a 1 at the beginning and end. Each interior number is calculated by adding the two numbers directly above it from the previous row. This process is repeated for as many rows as needed.
Can Pascal's Triangle be used to expand binomials?
Yes, Pascal's Triangle can be used to expand binomials through the binomial theorem. Each row of Pascal's Triangle represents the coefficients of the expanded terms of a binomial raised to the power corresponding to the row number, starting from 0. For example, the third row (1, 2, 1) corresponds to the expansion of (a + b)².
What is the relationship between Pascal's Triangle and Fibonacci Sequence?
There is a fascinating relationship between Pascal's Triangle and the Fibonacci Sequence. By summing up the numbers in the diagonals of Pascal's Triangle, you can produce the Fibonacci Sequence. Each diagonal sum represents a term in the Fibonacci Sequence, showcasing a hidden connection between these two famous mathematical concepts.
Are there any interesting patterns in Pascal's Triangle?
Pascal's Triangle is rich with patterns and properties. Besides the well-known vertical, horizontal, and diagonal sum patterns, it contains patterns related to prime numbers (for example, rows numbered with a prime number have all their elements divisible by that prime, except the 1s). Other patterns include the triangular numbers, hexagonal numbers, and the Sierpiński triangle pattern observed when coloring odd and even numbers differently.
Hello, world! I'm Esha Gupta, your go-to Technical Content Developer focusing on Java, Data Structures and Algorithms, and Front End Development. Alongside these specialities, I have a zest for immersing myself in v... Read Full Bio
Top Picks & New Arrivals
