Perfect Binary Tree
This article includes examples,implementations of Perfect Binary Tree and non perfect binary tree.
Binary tree data structures in computer programming store and organize the data efficiently, and it is popular for quick data retrieval. A binary tree has a tree-like structure and comprises nodes and edges. As its name suggests, a basic binary tree has a parent node and a maximum of two children of the parent node. Binary trees have numerous types and forms, like a complete binary tree, full binary tree, perfect binary tree, balanced binary tree, and skewed binary tree (left-skewed tree, right-skewed tree).In this article, we will learn about the perfect binary tree, examples of the perfect binary tree, properties of the perfect binary tree, and how to check whether a tree is a perfect binary tree.
Table of contents
Best-suited Data Structures and Algorithms courses for you
Learn Data Structures and Algorithms with these high-rated online courses
Perfect Binary Tree
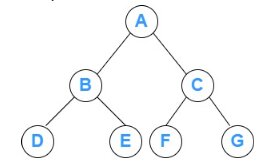
In a perfect binary tree, the internal node has exactly two child nodes, and all the child nodes are at the same level. Each level of the perfect binary is filled.
Example of a perfect binary tree
Ex1:
Ex 2:
Ex 3:
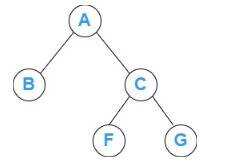
Example of non-perfect binary trees:
Ex 1:
Ex 2:



You can also explore: Queue Data Structure: Types, Implementation, Applications
Also explore: Data Structures and Algorithms Online Courses & Certifications
ou must explore: Deque – All That You Need To Know
You can also explore: Difference between Stack and queue
Properties of Perfect Binary Tree
- All internal nodes have a degree 2. Degree two means each node has two child nodes.
- A binary tree with no nodes or with a height of zero is known as a perfect binary tree.
- If the tree’s height is greater than zero, both tree subtrees should be of height (height-1) and non-overlapping.
- If the tree’s height is h, then the total number of leaves should be 2^h.
- Depth of the perfect binary tree is log(n).
- Total Number of leaf nodes= Number of non-leaf nodes + 1.
- Total Number of nodes in the tree is 2(h+1) – 1.
- Height of the tree is log (N+1)-1 = O(log (n)).
Implementation of Binary Tree in C
A perfect binary tree is a binary tree in which all leaf nodes are at the same depth and all non-leaf nodes have two children. Here is an example of how you might implement a perfect binary tree in C:
- First, define a struct to represent a node in the binary tree. The node should have fields for the data stored at the node, and pointers to the left and right children of the node:
struct Node { int data; struct Node *left; struct Node *right;};
- Next, define a function to create a new node. This function should allocate memory for the node using malloc, initialize the node’s data and left and right child pointers to NULL, and return a pointer to the new node:
struct Node* createNode(int data) { struct Node* node = (struct Node*) malloc(sizeof(struct Node)); node->data = data; node->left = NULL; node->right = NULL; return node;}
3. Now, you can use the createNode function to build the perfect binary tree. For example, to create the following perfect binary tree:
struct Node* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->left = createNode(6);root->right->right = createNode(7);
Let’s see the complete code in action:
#include <stdbool.h> // for the bool type#include <stdio.h> // for printf#include <stdlib.h> // for malloc
// Define a struct to represent a node in the binary tree.struct node { int data; // data stored at the node struct node *left; // pointer to left child struct node *right; // pointer to right child};
// Create a new node and return a pointer to it.struct node *createNode(int data) { // Allocate memory for the new node. struct node *node = (struct node *)malloc(sizeof(struct node)); // Initialize the node's fields. node->data = data; node->left = NULL; node->right = NULL;
// Return a pointer to the new node. return (node);}
// Return the depth of the given node in the binary tree.int depth(struct node *node) { // Initialize a counter to 0. int x = 0; // Traverse the tree starting from the given node. while (node != NULL) { // Increment the counter. x++; // Move to the left child of the current node. node = node->left; } // Return the depth of the node. return x;}
// Check whether the given binary tree is a perfect binary tree.// The function returns true if the tree is perfect, and false otherwise.bool perfect(struct node *root, int d, int level) { // If the root is NULL, the tree is empty, so it is a perfect binary tree. if (root == NULL) return true;
// If the root is a leaf node, check whether its depth is equal to d + 1. // If it is, then the tree is a perfect binary tree. if (root->left == NULL && root->right == NULL) return (d == level + 1);
// If the root has only one child, then the tree is not a perfect binary tree. if (root->left == NULL || root->right == NULL) return false;
// Recursively check the left and right subtrees. // If both are perfect binary trees, then the entire tree is a perfect binary tree. return perfect(root->left, d, level + 1) && perfect(root->right, d, level + 1);}
// Wrapper function to call the recursive perfect function.bool perfect(struct node *root) { // Get the depth of the tree. int d = depth(root); // Call the recursive function, starting at the root with level 0. return perfect(root, d, 0);}
int main() { // Create a binary tree.
struct Node* root = createNode(1); root->left = createNode(2); root->right = createNode(3); root->left->left = createNode(4); root->left->right = createNode(5); root->right->left = createNode(6); root->right->right = createNode(7);
The program begins by including the required header files and defining a struct node to represent a node in the binary tree. Each node has three fields: data to store the data at the node, and left and right pointers to the left and right children of the node.
Next, the program defines the newnode function, which creates a new node and returns a pointer to it. The function takes an integer data as input and uses the malloc function to allocate memory for the new node. It then initializes the node’s data and left and right child pointers to NULL , and returns a pointer to the new node.
The depth function takes a pointer to a node as input and returns the depth of that node in the binary tree. It does this by traversing the tree starting from the given node and counting the number of nodes it encounters until it reaches a leaf node (a node with no children).
The perfect function takes a pointer to the root of the binary tree and checks whether the tree is a perfect binary tree. It does this by performing a depth-first traversal of the tree and checking whether each node satisfies the conditions of a perfect binary tree. A perfect binary tree is a tree in which all leaf nodes are at the same depth and all non-leaf nodes have two children. The perfect function has three parameters: root, which is a pointer to the root of the tree; d, which is the depth of the tree; and level, which is the current depth in the traversal.
The main function creates a binary tree and calls the perfect function to check whether it is a perfect binary tree. If the tree is perfect, it prints “Tree is perfect binary tree”. Otherwise, it prints “Tree is not a perfect binary tree”.
How to Check IF a Tree is a Perfect Binary Tree or NOT?
To check whether a binary tree is a perfect binary tree, you can follow these steps:
- Define a struct to represent a node in the binary tree. The node should have fields for the data stored at the node, and pointers to the left and right children of the node.
- Write a function that takes a pointer to the root of the binary tree as input and returns a boolean value indicating whether the tree is a perfect binary tree or not.
- In the function, perform a depth-first traversal of the tree, starting from the root.
- At each node in the tree, check whether it satisfies the conditions of a perfect binary tree:
- If the node is a leaf node, check whether it is at the correct depth in the tree (all leaf nodes in a perfect binary tree are at the same depth).
- If the node is not a leaf node, check whether it has two children. If it does not, the tree is not a perfect binary tree.
- If the function reaches a leaf node and the depth of the node is correct, or if it reaches a non-leaf node with two children, continue the traversal. If the function encounters any other condition, return false to indicate that the tree is not a perfect binary tree.
- If the function completes the traversal of the tree without encountering any of the conditions that would cause it to return false , return true to indicate that the tree is a perfect binary tree.
Here is an example of how you might implement this in C:
#include <stdbool.h>#include <stdio.h>#include <stdlib.h>
// Define a struct to represent a node in the binary tree.struct Node { int data; struct Node *left; struct Node *right;};
// Create a new node and return a pointer to it.struct Node* createNode(int data) { // Allocate memory for the new node. struct Node* node = (struct Node*) malloc(sizeof(struct Node)); // Initialize the node's fields. node->data = data; node->left = NULL; node->right = NULL;
// Return a pointer to the new node. return node;}
// Check whether the given binary tree is a perfect binary tree.// Returns true if the tree is perfect, and false otherwise.bool isPerfectBinaryTree(struct Node* root) { // If the root is NULL, the tree is empty, so it is a perfect binary tree. if (root == NULL) { return true; } // If the root is a leaf node, then the tree is a perfect binary tree. if (root->left == NULL && root->right == NULL) { return true; } // If the root has only one child, then the tree is not a perfect binary tree. if (root->left == NULL || root->right == NULL) { return false; } // Recursively check the left and right subtrees. // If both are perfect binary trees, then the entire tree is a perfect binary tree. return isPerfectBinaryTree(root->left) && isPerfectBinaryTree(root->right);}
int main() { // Create a binary tree. struct Node* root = NULL; root = createNode(1); root->left = createNode(2); root->right = createNode(3); root->left->left = createNode(4); root->left->right = createNode(5); if (isPerfectBinaryTree(root)) { printf("Tree is perfect binary tree\n"); } else { printf("Tree is not a perfect binary tree\n"); } return 0;}
Contributed by Kanika Joshi
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio