Prioritizing Tasks: The Use of Heap Data Structure

The use of heaps in algorithms can help you manage your priority list and focus on the most important tasks. Read this article to learn how to use a heap in algorithms.

Heap is a unique linear tree-based data structure in which the tree is always fully constructed. Max heaps and Min heaps are two sorts of heaps. The max-heap will have a root node valued higher than its sub-tree, while the min-heap will have a root node valued lower than its sub-tree.

Read: What is Data structure?

Table of Content

• Introduction: Heap Data Structure
• Characteristics of a Heap Tree
• Max.heap and Min.heap
• Pros: Heap Data Structure
• Cons: Heap Data Structure
• The Use of a Heap in Algorithms

Introduction: Heap Data Structure

A particular kind of tree data structure is called a heap. A binary tree whereby every tree element has a minimum of two offspring is known as a heap. The source node located at the peak of this tree would indicate the smallest kid, and the nodes situated at the bottom would be the eldest iterations of relatives represented in the tree. 

A genetic ancestry tree is a typical illustration of a binary tree in which each child has precisely two parents. In most cases, heaps are either min-heap or max-heap trees, which will be discussed in the following section.

Heap tasks:

• Heapify: It is a technique for making a heap out of an array.
• Insertion: time-consuming procedure of adding a new element to a current heap (log N).
• Deletion: arranging the heap and providing the unit with time complexity O after removing the element with the greatest priority or at the top of the heap (log N).
• Peek: to look at or locate the piece at the front of a pile

Explore- Data Structures and Algorithms Courses

Characteristics of a Heap Tree

There are a few characteristics that all heaps have, irrespective of whether they are min-heap trees or max-heap trees. Because each sibling in max-heap trees has a bigger value than its early years’ educators and each father in min-heap trees has a lower value than its kid’s nodes, there is an inferred hierarchy between each parent node and its children.

• Ordering

A heap tree’s usefulness depends on the nodes’ arrangement. All heap tree conditions must be met for each subset in a heap tree. Every parent node in a min-heap tree is lower than its offspring. As an outcome, a binary tree is created, with the root node being the simplest model and the branches (the elements at the bottom of the tree) being the greatest values. Every parent node in a max-heap tree is bigger than its siblings. Consequently, a binary tree is created, with the root node being the biggest element and the leaves being the shortest.

• Structure

Heap trees have the same structure as a typical binary tree. The result is a tree with a maximum of two offspring for each parent node. The unique structure of min-heap trees makes it possible to reach the substring in O(1) time quickly. In a max-heap tree, finding the biggest member is also O (1).

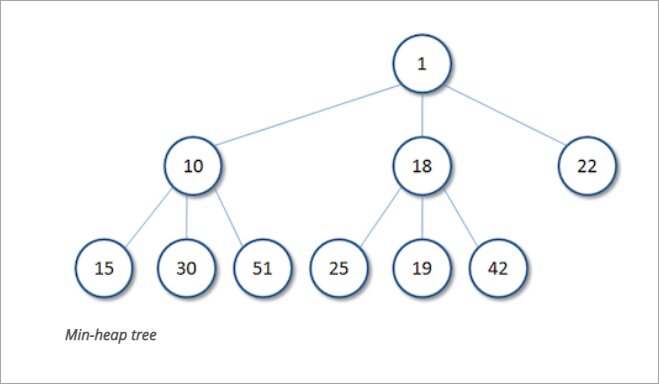
Max.heap and Min.heap

Based on whether it is a max-heap or a min-heap, a heap is a full binary tree in which the nodes are arranged differently.

• Max Heap: Each node’s value must be higher than its children’s. The maximum value is kept in the root node of the max heap.
• Min Heap: A node’s value should be lower than its offspring in the minimum heap. The minimal value is kept in the root node.

The root node of binary trees, such as min-heap trees and max-heap trees, is known as the key. The lowest value in the entire tree must be in the key of a min-heap tree. Additionally, the offspring of every preferred parent must be more significant than the parent node. The greatest value in the tree must be in the key of a max-heap tree. The offspring of each parent node must also be shorter than the neighbour nodes. 

In a max-heap tree, the youngest sibling would have the highest value, and each age would have lesser numbers than the children it produced, with the eldest relatives having a lower number than any subsequent generations. This is similar to the ancestor tree example from before.

Example:

Assume that R is the root element’s name and that the root’s left and right subtrees are already heaps. The following graphic represents this circumstance:

Node R’s two subtrees are heaps. R must now be lowered to its suitable position inside the stack.

There are two options in this situation.

• R’s value is larger than or equal to its two offspring’s. Construction is finished in this instance.
• R’s value is lower than any or both of its offspring.

R ought to be swapped out for the more valuable kid. R could still be smaller than one or both of its (new) children, but the outcome will be a heap. In this instance, we keep “pushing down” R until it surpasses its offspring or becomes a leaf node, in which case we stop. The exclusive method of siftdown is used to carry out this operation.

According to this method, which presupposes that the subtrees are already heaps, a full algorithm may be produced by visiting the nodes in a sequence in which the cluster children are examined before the node. Working from the high index of the collection to the low index is one quick technique to do this. The construction procedure can begin with the first internal node in the array’s centre, as the build process does not need to visit the leaf nodes.

The process is turned into the following:

The following formula calculates the summation of total distances:

It is known that the closed-form result of the total on the right is about 2. Hence the worst-case execution time of this method is (n) time. In comparison, creating the heap one member at a time would, in the worst scenario, cost nlogn. Moreover, it is quicker than the (nlogn) average-case and (n2) worst-case times needed to construct the BST.

Eliminating an item from the heap or altering its priority:

The cost of removing the highest element is (logn) in both the median and worst scenarios since the heap is logn levels deep.

Must Read – 8 Most Important Data Structures Every Programmer Must Know

Pros: Heap Data Structure

1. Effective element input and removal: The heap data structure enables effective element insertion and removal. A node is inserted into the heap at the bottom, and then, using the heapify process, it is raised to its proper position. The heap is reformed using the heapify procedure when an element is eliminated; the bottom element then substitutes it.
2. Storage capacity: Since the heap data structure stores components in a full binary tree structure, it uses lower memory than alternative data structures like clustering or arrays.
3. Heapsort algorithm: The heap data structure is the foundation for the efficient sorting algorithm known as the heap-sort, which has a worst-case computation time of O. (n log n).
4. Effective priority queue: A priority queue is frequently implemented using the heap data structure, where the primary concern component is always at the highest level of the heap. The heap is an effective data structure for building priority queues because it offers constant-time access to the element with the greatest priority.
5. Access to the highest or lowest element is always guaranteed: In a max-heap, the highest element is always the highest element, and in a min-heap, the highest element is always the lowest element. This is helpful for algorithms that need a reference to the extreme values since it guarantees access to either the heap’s maximum or smallest element.

Cons: Heap Data Structure

1. Limitation of adaptability: Since the heap data structure is intended to retain a particular sequence of components, it is not very versatile. As a result, it might not be appropriate for some applications that call for more adaptable data structures.
2. Not great for querying: While the heap data structure offers rapid access to the highest element, it is not suitable for looking for a particular element in a heap. Looking for an item in a heap involves navigating the entire tree, which has a temporal complexity of O(n) (n).
3. Not a reliable data structure: The heap data structure is not secure, which implies that when the heap is built or updated, the comparative position of equal components cannot be retained.
4. Memory management: The heap data structure necessitates the constant allocation of memory, which presents a problem in some memory-constrained systems. Moreover, managing the memory assigned to the heap might be difficult and error-prone.

The Use of a Heap in Algorithms

Scheduling Algorithms

Algorithms for task scheduling that prioritize or plan tasks according to deadlines employ the heap data structure. The heap data structure is beneficial for work scheduling applications because it enables quick access to the task with the greatest priority.

Graph Algorithm

Many graph algorithms, including Dijkstra’s, Prim’s, and Kruskal’s algorithms, use the heap data structure. The heap data structure may be used to construct priority queues efficiently for these methods.

Memory Management

Memory management systems employ the heap data structure to allocate and deallocate memory dynamically. The memory blocks are kept in a heap. The heap data structure manages them effectively and distributes them to applications as required.

Priority Queues 

Priority queues are frequently implemented using the heap data structure. Here, entries are piled up and sorted according to priority. This makes it an effective data structure for handling events and activities that require prioritizing since it enables constant access to the element with the greatest priority.

Heapsort Algorithm

The heap data structure is the foundation for the efficient sorting algorithm known as the heapsort, which has a worst-case computation time of O. (n log n). Many applications, such as database mining and quantitative simulation, employ the heapsort method.

Conclusion

We have covered several heap data structure applications in this post. In practice, heaps are employed when retrieving and managing components according to their priority effectively is necessary. Heaps are effective since they can obtain, add, and delete elements quicker than a linear search in O(log n) time instead of O(n) time. Moreover, heaps may be easily implemented and used for various algorithms and data structures.

Contributed By: Furkan Khan