RELU and SIGMOID Activation Functions in a Neural Network
Activation functions are one of the most important features of an artificial neural network. In this article we will briefly discuss about activation function and two of important types ReLU and Sigmoid Activation functions in complete detail.
This blog has a very well-seasoned approach with the Sigmoid and Relu Activation functions, as they have been cited as examples from my real-time notebook in Kaggle data source with the underlying source code in python for positive and negative slopes as well as gradient descent alongside the slopes and drills down to the biological neurons as they send spikes to other neurons and send impulses whether to activate the other neurons or not which is on or off. And thus would coin the term Activation function. In this article we will explore Relu and Sigmoid function.
Must Check: Top Neural Network Online Courses and Certifications
So, how do you define an Activation function?
Let’s explore the article
Table of Content
Best-suited Data Science courses for you
Learn Data Science with these high-rated online courses
What is an Activation Function?
An activation function is a very important feature of an artificial neural network that is used to determine what to do with the neurons, i.e., whether they will be activated or not. In artificial neural networks, the activation function defines the output of that node given an input set or just a single input.
One of the reasons for evincing interest in us is the hope to understand our mind, which emerges from neural processing in our brain. Advances in machine learning have been achieved in recent years by combining massive data sets and deep learning techniques.is yet another reason.
Types of Activation Functions
- Linear Activation Function
- Non-Linear Activation Function
- Sigmoid Activation Function
- Tanh Activation Function
- ReLU Activation Function
- Leaky ReLU
- Parametric ReLU
Also Read: Different Types of Neural Networks in Deep Learning
Weights and Inputs
In Linear and Logistic Regression, weights are the set of adaptive parameters in an artificial neuron model. These weights act as a multiplier on the inputs of the added neuron. The linear combination of these inputs is the sum of weight times the input.
Let’s take the shopping bill analogy to understand the above concept:
Shopping bills are a linear combination of the number of units purchased and the price of each unit, i.e., the total amount is each item’s product by its price and then added.
If there’s a neuron with six inputs (analogous to the amounts of the six shopping items: potatoes, carrots, beetroots, etc.), input1, input2, input3, input4, input5, and input6, we thereby need six weights. The weights are similar to the prices of the items. They worry about weight1, weight2, weight3, weight4, weight5, and weight6. We would want to include an intercept term as we did in linear regression. This can be considered an example of a fixed additional charge due to processing a credit card payment, for example, in the shopping cart analogy.
We could then calculate the linear combination as follows: linear combination = intercept + weight1 × input1 + … + weight6 × input6, whereby the … (Three dots) means that the sum includes all the terms from 1 to 6)
Similar to linear and logistic regression, weights in neural networks learn from the data.
Activations used in Activation Function and Outputs
After computing the linear combination, the neuron takes the linear combination (weights and biases) and puts it through a so-called activation function. Accurate examples of the activation function include:
Identity Function
Output the linear combination of weights and biases.
Step Function:
If the input is greater than zero, turn/send a pulse to activate (ON), otherwise (OFF).
Sigmoid Function:
A soft, smooth version of the step function.
Neural Activation:
Communication in biological neurons is done by sending out sharp, electrical pulses called “spikes” spontaneously so that at any given time, the outgoing signal is either on or off (1 or 0). The step function mimics this kind of behavior. However, artificial neural networks tend to use activation functions that output a continuous numerical activation level at all times, such as the sigmoid function.
The output of the neuron, established by the linear combination and the activation function, can be used to extract a prediction or a specific decision. For instance, if the network is designed to identify a HALT sign in front of a self-driving car, the input could be the image pixels, the photo captured by a camera attached to the front of the car itself. The output could activate a stopping procedure using an Activation function that stops the car before the sign.
The neural network adaptation occurs when the neurons’ weights are adjusted to make the network produce the correct outputs, the same as in linear or logistic regression. Many neural networks are very huge, and the largest contains hundreds of billions of weights. Optimizing them could be a real Hercules task that requires massive amounts of computing power.
Also Read: Introduction to Neural Networks in Deep Learning
Most ML models use rectified linear units (ReLU) as non-linearity instead of Sigmoid function in a deep neural network. The question is, why? That’s what we’re here to find out:
What is an activation function?
A nonlinear function used to send the output signal either on or off to a neuron is known as an activation function.
Sigmoid Function:
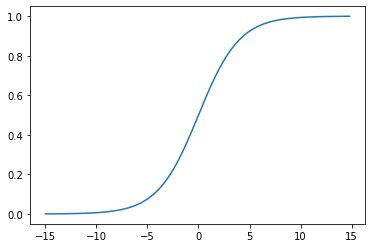
A mathematical function that transforms the values between the range 0 and 1 is known as the sigmoid function. It is an S-shape curve that mainly used with non-linear activation functions and is also known as the Sigmoidal Curve.
It is a smooth and continuously differentiable function that gives output after activation. This is a nonlinear function, almost like an S- shape. The typical reason to use the sigmoid function is its activation value between 0 and 1. It is used explicitly for models where we have to predict the probability as an output, especially statistical predictions. As the probability lies between the range 0 and 1 so, the sigmoid function is the best choice. Sigmoid is one of the most widely used non-linear activation functions. Sigmoid translates the values between the range 0 and 1.
Here is the mathematical expression for sigmoid-
f(x) = 1/(1+e^-x)
As we know, the sigmoid function sends the output values between 0 and 1. Statistically, a significantly negative number passed through the sigmoid function becomes 0, and a large positive number becomes 1.
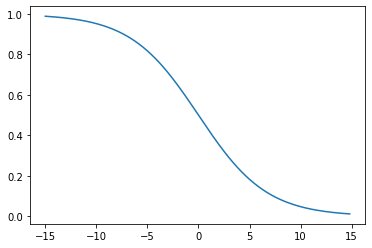
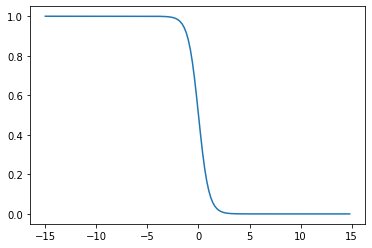
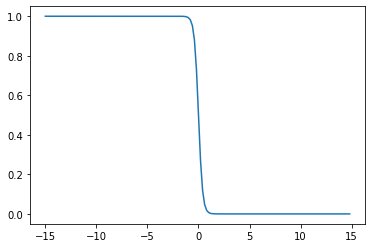
Now, we will analyze the source code and the graph of the sigmoid function for high positive and negative values and the relevant slopes for the same and for that we will use dummy dataset of sofa set image.
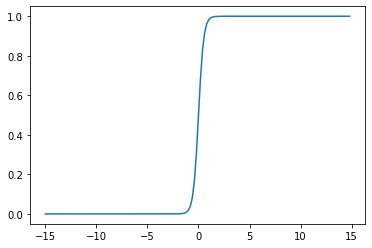
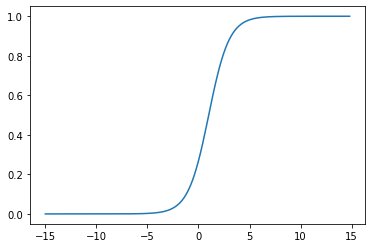
import numpy as npfrom matplotlib import pyplot as pltdef sigmoid(w,b,x): return 1.0/(1.0+np.exp(-(w*x+b)))x = np.arange(-15.0, 15.0, 0.2)y = sigmoid(-0.3,0,x)plt.plot(x,y)plt.show()
y = sigmoid(-2,0,x)plt.plot(x,y)
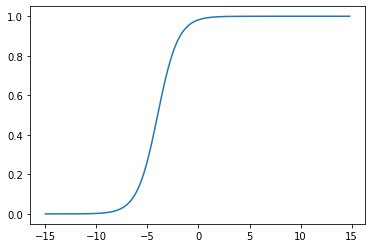
y = sigmoid(-5,0,x)plt.plot(x,y)
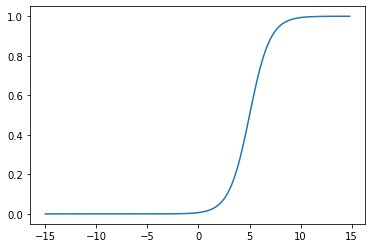
y = sigmoid(.5,0,x)plt.plot(x,y)
y = sigmoid(4,0,x)plt.plot(x,y)
y = sigmoid(1,4,x)plt.plot(x,y)
y = sigmoid(1,-1,x)plt.plot(x,y)
y = sigmoid(1,-5,x)plt.plot(x,y)
y = sigmoid(.5,1.2,1)print(y)0.845534734916465
Code for sigmoid function in Python
def sigmoid(x,Derivative=False): if not Derivative: return 1 / (1 + np.exp (-x)) else: out = sigmoid(x) return out * (1 - out)( The one to produce the derivatives)ordef sigmoid(x): return 1 / (1 + np.exp(-x))
While writing code for sigmoid, we could use this code for both forward propagations and compute derivatives.
ReLU
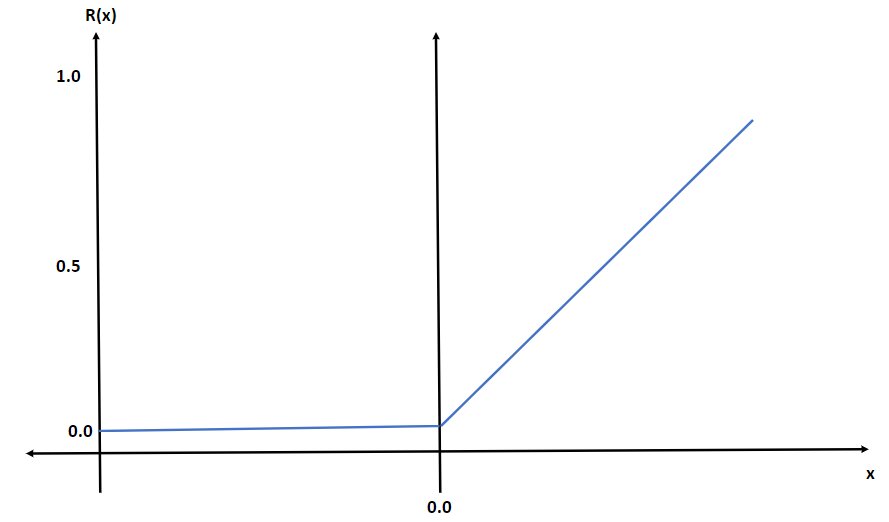
ReLU Rectified Linear Unit. This is the most frequently used activation unit in deep learning. R(x) = max(0, x) . Thereby, if x < 0, R(x) = 0 and if x ≥ 0, R(x) = x. It also enhances the convergence of gradient descent compared to sigmoid or tanh activation functions.
Advantage of ReLU Function:
- It doesn’t allow for the activation of all of the neurons at the same time.
- i.e., if any input is negative, ReLU converts it to zero and doesn’t allow the neuron to get activated. This means that only a few neurons are activated, making the network easy for computation.
- Rectifies the vanishing gradient descent problem.
Is ReLU Linear or Nonlinear
As Relu is defined by max(0,x) i.e.
R(x) = 0, if x < 0, and
R(x) = 0, if x >= 0
hence, the graph of ReLU, would be like:
So, there is no way to get the graph as a single straight line, therefore ReLU is a nonlinear function.
Sigmoid vs ReLU Activation Function:
Training deep neural nets was not possible using sigmoid-like activation functions.
ReLU (amidst other things) made the training of deeper nets feasible. And since then, we have been using ReLU as a default activation function for the hidden layers. So exactly what makes ReLU a better and best choice over Sigmoid?
RELU vs. Sigmoid:
| Parameters | Sigmoid | Relu |
| Role of Slope/Plateau in sigmoid/Relu activation functions | Once the sigmoid function reaches towards the left or the right Plateau, it would be rather impossible to do a backward propagation through the Slope as the derivative would reach to a 0. | Relu would saturate only while the input is less than zero which rather could be reduced by the use of Leaky ReLus only with respect to the Relu derivative ending the activated neuron during forward propagation to 0 for a larger gradient and thus ending with negative weights and biases during forward propagation again which would be a dead neuron in biological terms.To avoid this scenario, we multiply x by a constant value of 0.01 in Leaky ReLus. |
| Vanishing gradient problem | Sigmoid has this vanishing gradient problem as the output of this derivative is not zero-centered.power mathematical operations are consuming most of the time thereby increasing model complexity | Relu has a gradient of 1 when the input>0, else a gradient of zero, otherwise. Thereby, we could multiply a mix of ReLus in the backprop equations to maintain 1 or 0 for the gradient .Apparently, there is no vanishing gradient for Relus. |
| Computational power | Slow in training an ML model as the derivative is complex and requires huge computations. | Fast when compared to sigmoid as the derivative is a constant and constants always play a key role in training the ML model.Derivative is simply 0 or 1 based upon the input. |
| Model performance | The performance of a NN model is based upon a non- linear activation function and to backward propagate and adjust the weights and produce the desired result which is the actual output and the model retrains itself viably to adjust the difference between the actual and the desired output. The computational power of the sigmoid derivative is complex and always results in a zero when the x increases. Hence the gradient is 0 and when multiple layers are multiplied thereby the gradient would be zero thereby resulting in poor model performance.However, for classification problems like the autoencoder in tensorflow we could use sigmoid activation function in the final output layer. | Relu can be used in the hidden layers between the input layer and output layer because when x>0 the gradient would be either 1 ,or a 0, when x<= 0. This decreases the vanishing gradient problem thus improving the model performance and when multiple ReLus activated neurons multiply, the result of the derivative is simply a 0 or a 1 exception being the negative weights and biases, which could be solved by leaky ReLus with x being multiplied by a constant value of 0.01 And thereby reducing the vanishing gradient problem with NN model performance improvement during forward propagation. |
| Efficiency of NN | Very good. | Good with Leaky ReLus in a NN. |
| Type | Non-zero centered activation function | Derivative resorts to either 0 or 1.Leaky ReLus are best . |
Conclusion
ReLU boasts of training complex models/neural networks with constant values compared to sigmoid.
Relu exhibits better efficiency:
An advantage of ReLU, despite avoiding the vanishing gradients problem, is that it has a much lower run time max(0,f) and runs much faster than any sigmoid function.
Author: Aswini S.
FAQs
Why is Relu better than SIGMOID?
It is simple and faster to compute and does not activate all the neurons simultaneously. Even the derivation of Relu is easy to calculate, which makes a significant difference in training and inference time.
What makes the ReLU function more appropriate in some cases over a Sigmoid activation function?
ReLU prevents gradients from saturating in deep networks and thus mitigates the risk of vanishing gradients. Ideally, you should be coupling ReLUs and sigmoidal activation functions since sigmoidal activation functions are better at capturing nonlinearities. Clarification: you should mix ReLUs and sigmoidal activation functions across layers; each layer should use either of the two activations and still have the same activation for each hidden unit.
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio