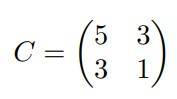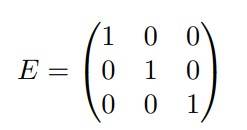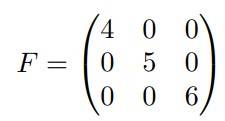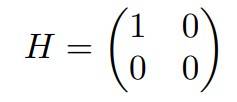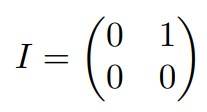Square Matrix Fundamentals: A Quick Guide

Explore the essentials of a square matrix: dive into its definition, properties, and real-world applications. Unlock the power of these fundamental mathematical tools.

 

A square matrix is a special matrix with an equal number of rows and columns, creating a perfect square grid of elements. 
Square Matrix Example

• It is used to represent linear transformation, which is mapping from one vector space to another. 
• For Example, A 2D rotation matrix R that rotates points by an angle theta is given by:

• Square matrices are used to solve the system of linear equations using the linear decomposition method.
• For Example, A system Ax = B can be solved by finding the inverse of A (if it exists) and then calculating x = A^-1 B.
• A 2 x 2 square matrix is used as the key for encryption, where the matrix is used to transform pairs of letters into encrypted pairs.

Square Matrix Properties

Diagonal Dominance

A matrix is diagonally dominant if, for every row of the matrix, the magnitude of the diagonal entry in a row is greater than or equal to the sum of the magnitude of all the other (non-diagonal) entries in that row.

Let's take an example to get a better understanding.

In the above matrix:

First Row:

|6| >= |-1| + |0|,

Second Row

|5| >= |-1| + |-2|,

Third Row

|4| >= |0| + |-2|

Which makes it diagonally dominant.

Symmetry

A square matrix is said to be a symmetric matrix if it is equal to its transpose.

Example

Here, C = C^T

Skew-Symmetry

A square matrix is said to be a skew-symmetric matrix if it is equal to its negative transpose.

Example:

Here, D = -D^T

Trace

The trace of the square matrix is the sum of its diagonal elements. If A is any matrix, then it is represented by tr(A).

Let's find the trace of the above matrices.

tr(C) = 5 + 1 = 6

tr(D) = 0 + 0 = 0

Invertibility

A square matrix A is said to be an invertible matrix when there exists another matrix B such that:

AB = I = BA,

where I is an identity matrix.

If the above condition is satisfied, then B is said to be the inverse of A and represented by A^-1.

Eigen Value and Eigen Vector

The eigenvalue in a square matrix is a scalar quantity that when multiplied by an eigenvector, gives the same result as when an eigenvector is multiplied by the matrix.

In simple terms, if k is an eigenvalue, v is an eigenvector, and A is any matrix, then:

Av = kv

Types of Square Matrix

There are different types of square matrices, such as Identity Matrix, Diagonal Matrix, Symmetric Matrix, Skew-Symmetric Matrix, Orthogonal Matrix, Idempotent Matrix, Nilpotent Matrix, and Invertible Matrix.

In this section, we will discuss these matrices in detail.

Identity Matrix

A square whose all diagonal elements are equal to one and all off-diagonal elements are zero is known as an Identity Matrix.

Diagonal Matrix

A square matrix is said to be a diagonal matrix if all off-diagonal elements are zero.

Orthogonal Matrix

A square matrix is said to be an orthogonal matrix if it returns an identity matrix when multiplied by the transpose of that matrix.

i.e., GG^T = I = G^TG

Idempotent Matrix

A square matrix, when multiplied by itself, returns itself, is known as an idempotent matrix.

Here, HH = H.

Nilpotent Matrix

A matrix, when raised to a certain power (denoted as k), results in the zero matrix, which is known as the nilpotent matrix.

Here, I² = 0.

Operations on Square Matrix

For this section, let's consider two square matrices.

Matrix Addition

Two matrices of the same size can be added together by adding their corresponding elements.
Example:

Matrix Multiplication

The product of two square matrices is a new matrix where each element is the sum of the product of elements from the rows of the first matrix and the column of the second matrix.
Example

Matrix Transpose

The transpose of a matrix is obtained by interchanging rows and columns, respectively.
Example:

Inverse of a Matrix

The inverse of a matrix A is another matrix A^-1 such that A*A^-1 = A^-1*A = I, where I is the identity matrix.

Conclusion

In conclusion, the square matrix is a key player in mathematics and beyond. Its unique properties enable efficient problem-solving across various disciplines, proving that these orderly arrays of numbers are as versatile as they are vital.