Creating XOR Gate Using NAND Gate

Have you ever thought about making an XOR gate using only NAND gates? It's quite fascinating that with a smart setup of NAND gates, you can achieve the exclusive OR operation, showing just how crucial NAND gates are in the world of digital circuits. Let's understand more!

Creating an XOR gate using NAND gates is a classic example of gate manipulation in digital logic design. An XOR (Exclusive OR) gate outputs true only when its two inputs differ. Let's explore how.

Also, Explore Universal Logic Gates

XOR Gate

An XOR Gate has a single output and two or more inputs & is called exclusive OR. The output is 1 only when an odd number of inputs are 1. The XOR gate’s Boolean logic for inputs A and B is Z=A⊕B = ~A.B+A.~B.

Truth Table:

Symbol :

 

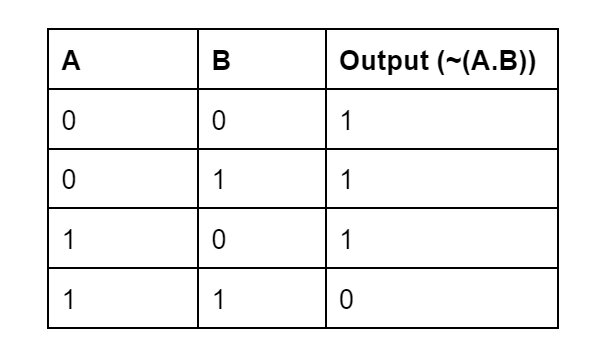
NAND Gate

A NAND gate has a single output and two or more inputs. The output is 0 only when all of the inputs are 1. For all other combinations, the output is 1. The NAND gate’s Boolean logic is Z= ~ (A.B) for inputs A and B.

Truth Table :

Symbol :

 

 

Let’s Create an XOR Gate Using the NAND Gate

To create an XOR gate using NAND gates, you’ll need four NAND gates.

Pre-requisites

• Simulation software (like Multisim or LTspice) or digital logic gates kit
• Understanding of logic gate symbols and truth tables

Let’s Set Up the Circuit

STEP 1:

NAND Gate 1: Connect input A to both inputs of the first NAND gate. This will give us an output ~A which is NOT A

The output of this gate will be: O_1​=∼(A⋅A) = ~A

STEP 2:

NAND Gate 2: Connect input B to both inputs of the second NAND gate. This will give us an output ~B which is NOT B.

The output of this gate will be: O₂​=∼(B.B​) = ~B

STEP 3:

NAND Gate 3: Connect ~A (output of gate 1) and B to the inputs of the third NAND gate. This gives us an output which is one part of the final XOR expression.

The output of this gate will be: O₃​=∼(~A.B​)

STEP 4:

NAND Gate 4: Connect A and ~B (output of gate 2) to the inputs of the fourth NAND gate. This gives us another output which is another part of the final XOR expression.

The output of this Gate: O_4​= ~(A. ~B)

STEP 5:

Connect O_3​ and O₄​ to another NAND gate to create the final XOR output.

Output: Y = ~(O₃.O₄) = A⊕B

Let’s Draw the Circuit for the Same

Where ⊕ represents the XOR (Exclusive OR) operation in Boolean algebra and digital logic design

Let’s Test Via Truth Table

Create a truth table for your new XOR gate to verify its functionality.

The truth table for an XOR gate is:

Where XOR = A⊕B (Y) = ~(O₃.O₄), Thus our functionality is verified.

Thus, we created an XOR Gate using the NAND Gate & it is a valid and effective approach in digital logic design.