Adjacency Matrix For Graphs
The adjacency matrix also called the connection matrix, is a matrix containing rows and columns which is used to represent a simple labelled graph. In this article, we will study the Adjacency Matrix for different types of graphs.
An Adjacency Matrix is a method of representing graphs in matrix form. The adjacency matrix plays a vital role in describing finite graphs, making them easier to understand and compact representation. A graph is a collection of nodes and edges. In an adjacency matrix, nodes and edges of the graph are used to describe the graph. The nodes are the graph’s vertices, whereas the edges are the finite set of ordered pairs. In this article, we will discuss the Adjacency Matrix For Graphs, the representation of the adjacency matrix, How to create an adjacency matrix from the graph, and the adjacency matrix for both undirected and directed graphs.
Table of contents
Best-suited Data Structures and Algorithms courses for you
Learn Data Structures and Algorithms with these high-rated online courses
Adjacency Matrix
An adjacency matrix is simply a square matrix or connection matrix used to describe a finite graph in matrix format. It maps the connection between the edges and vertices of the graph in a two-dimensional matrix.
If a graph is of n vertices or nodes, its corresponding adjacency matrix would be n x n size. Each matrix entry indicates the number of matrices from one vertex to another. It represents a weighted graph in matrix format as adj [x][y] = w, meaning there is an edge from vertex x to vertex y with a weight of w.
Read Later
Also explore: Data Structures and Algorithms Online Courses & Certifications.
Also read: Queue Data Structure: Types, Implementation, Applications
Adjacency matrix representation
If there is an undirected graph G that has n vertices, then the adjacency matrix A will be of n x n size, and if there is an entry in the matrix A = a[i]j], it will be defined as-
if there exists a path from vertex i to vertex j,
a[i][j] = 1
else
a[i][j] = 0
Some important points:
- If a path exists from vertex i to vertex j, then the entry at a[i][j] will be 1.
- If there is no path from vertex i to vertex j, the entry at a[i][j] will be 0.
- If all the diagonal entries of the matrix are 0, then the graph has no self-loops.
- If the value of the ith row and jth column is equal to the jth row and ith column, then the adjacency matrix is symmetric for the respective graph.
Also Read: Implementing ArrayList in Java
Also Read: ArrayList in Java
How to create an adjacency matrix?
After knowing what the adjacency matrix is and its representation, let’s learn how to create an adjacency matrix from a given graph.
Assume a graph G with n number of a vertex. Then the corresponding adjacency matrix is represented as
A=
| a11 | a12 | a13 | ….. | a1n |
|---|---|---|---|---|
| a21 | a22 | a23 | ….. | a2n |
| a31 | a32 | a33 | …. | a3n |
| :: | :: | :: | :: | :: |
| an1 | an2 | an3 | ….. | ann |
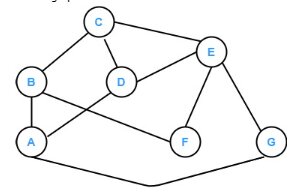
Creating Adjacency matrix for Undirected graph
In an undirected graph, edges do not have any directions, so the edge is assumed to be bi-directional. If there is an edge connecting nodes A and B, it is assumed that the data can be transferred from A to B and B to A.
Consider the following undirected graph, and we will design the corresponding adjacency matrix for that graph.
The undirected graph has seven vertices, then the matrix will have a total of 7 x 7 entries, and the corresponding adjacency matrix for the above undirected will be as
| i↓ j→ | A | B | C | D | E | F | G |
| A | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| C | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| D | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| E | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| F | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| G | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Creating Adjacency matrix for Directed graph
In a directed graph, edges are associated with the directions. Consider the following directed graph and design an adjacency matrix for the corresponding graph.
The directed graph has six vertices, so there will be 6 x 6 entries in the adjacency matrix.
| i↓ j→ | A | B | C | D | E | F |
| A | 0 | 1 | 0 | 0 | 0 | 1 |
| B | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 0 | 0 |
| D | 1 | 0 | 0 | 0 | 1 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 0 | 1 | 1 | 0 |
Algorithm
int main() { int adjMatrix[V][V];
init(adjMat); addEdge(adjMat, 0, 1); addEdge(adjMat, 0, 3); addEdge(adjMat, 2, 1); addEdge(adjMat, 2, 3); addEdge(adjMat, 3, 1);
printMatrix(adjMat);
return 0;}
#include <stdio.h>#define V 4
void init(int arr[][V]) { int i, j; for (i = 0; i < V; i++) for (j = 0; j < V; j++) arr[i][j] = 0;}
void addEdge(int arr[][V], int i, int j) { arr[i][j] = 1; arr[j][i] = 1;}
void printMatrix(int arr[][V]) { int i, j;
for (i = 0; i < V; i++) { printf("%d: ", i); for (j = 0; j < V; j++) { printf("%d ", arr[i][j]); } printf("\n"); }}
Illustration of the above code:
Example
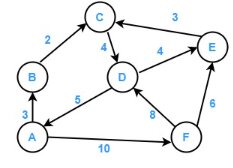
Consider a weighted directed graph, and design an adjacency matrix for that graph.
Adjacency Matrix for the weighted graph:
| i↓ j→ | A | B | C | D | E | F |
| A | 0 | 3 | 0 | 0 | 0 | 1 |
| B | 0 | 0 | 2 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 4 | 0 | 0 |
| D | 5 | 3 | 0 | 0 | 4 | 0 |
| E | 0 | 0 | 3 | 0 | 0 | 0 |
| F | 0 | 0 | 0 | 8 | 6 | 0 |
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio
Top Picks & New Arrivals
