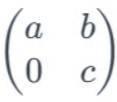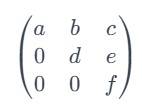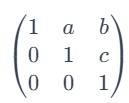Upper Triangular Matrix: Definition, Example, and Properties
A triangular matrix is a special type of square matrix where all the elements below or above the principal diagonal are always zero. There are different types of triangular matrices, but they are broadly classified into:
- Upper Triangular Matrix
- Lower Trinagular Matrix
This article will discuss upper triangular matrices in complete detail, starting with their definition, examples, and properties.
So, without further delay, let's get started.
Table of Content
- What is an Upper Triangular Matrix
- Example of Upper Triangular Matrix
- Properties of Upper Triangular Matrix
- Special Type of Upper Triangular Matrix
- Real-Life Examples of Upper Triangular Matrix
What is an Upper Triangular Matrix?
The upper triangular matrix is a type of triangular matrix where all the elements below the principal diagonal are zero.
In simple terms, a matrix U = {uij}nxn is known as an upper triangular matrix if and only if uij = 0, for all i>j.
i.e.,
Best-suited Maths for Data Science courses for you
Learn Maths for Data Science with these high-rated online courses
Example of Upper Triangular Matrix
A simple 2x2 Upper Triangular Matrix
A 3x3 Upper Triangular Matrix
The diagonal element can contain any value, including zero. If all the main diagonal elements are zero, then the matrix is known as a Strictly Upper Triangular Matrix.
Example of a Strictly Upper Triangular Matrix
Properties of Upper Triangular Matrix
- Elements below the principal diagonal in the Upper Triangular Matrix are always zero.
- When two Upper Triangular Matrix are added or subtracted, the result is also an Upper Triangular Matrix.
- The product of two Upper Triangular Matrix is again an Upper Triangular Matrix.
- The inverse (if it exists) of an Upper Triangular Matrix is again an Upper Triangular Matrix.
- The determinant of an Upper Triangular matrix is simply the product of the diagonal entries.
- Eigenvalues of an Upper Triangular Matrix are the elements on the principal diagonal.
Special Types of Upper Triangular Matrix
Diagonal Matrix
A special type of upper triangular matrix, where the elements below and above the principal diagonal are always zero.
Unit Upper Triangular Matrix
An Upper Triangular Matrix, where all the principal diagonal elements are equal to one.
Strictly Upper Triangular Matrix
An Upper Triangular Matrix, where all the principal diagonal elements are equal to zero.
Block Upper Triangular Matrix
The matrix is divided into blocks. In Block Upper Triangular Matrix, blocks are square matrices, and the blocks below the principal diagonal are null matrices.
Real-Life Examples of Upper Triangular Matrix
| Industry/Sector | Description of Application | Scenario-Based Example |
|---|---|---|
| Computational Science | Used in algorithms for numerical solutions of linear equations, eigenvalue problems, and matrix decompositions. | Solving a system of linear equations using LU decomposition, where the upper triangular matrix simplifies the process. |
| Finance | Applied in financial modelling for solving systems of linear equations in risk management and pricing models. | In portfolio optimization, upper triangular matrices are used to calculate the covariance matrix of asset returns. |
| Engineering | Utilized in structural analysis and design, particularly in solving linear systems in finite element analysis. | Analyzing the stress on a bridge structure by solving a set of linear equations with upper triangular matrices. |
| Data Science | Employed in machine learning algorithms, especially in linear regression and optimization problems. | In linear regression, upper triangular matrices are used to compute the regression coefficients efficiently. |
| Physics | Used in quantum mechanics and other theoretical physics models for simplifying complex linear equations. | Simplifying the calculation of quantum states in a system using upper triangular matrices in quantum mechanics. |
| Computer Graphics | Applied in 3D graphics for transformations and rendering processes. | In 3D rendering, using upper triangular matrices for efficient computation of object transformations. |
| Telecommunications | Used in signal processing, especially in algorithms for filtering and data compression. | In digital signal processing, upper triangular matrices are used to filter audio or video signals efficiently. |
| Cryptography | Employed in certain encryption algorithms for efficient matrix operations. | Using upper triangular matrices in public key cryptography algorithms for faster computations. |
| Meteorology | Utilized in weather prediction models for solving large systems of linear equations. | In weather modelling, using upper triangular matrices to solve equations predicting atmospheric changes. |
| Economics | Applied in econometric models for analyzing economic data and forecasting. | In economic forecasting, upper triangular matrices are used to analyze time-series data for predicting market trends. |
Conclusion
This article briefly discussed an upper triangular matrix, its properties, and some special types of upper triangular matrices. At the end, we have also discussed some real-life applications of the upper triangular matrix.
Hope you will like the article.
Keep Learning!!
Keep Sharing!!















Vikram has a Postgraduate degree in Applied Mathematics, with a keen interest in Data Science and Machine Learning. He has experience of 2+ years in content creation in Mathematics, Statistics, Data Science, and Mac... Read Full Bio