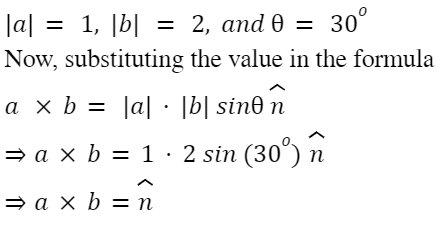Cross Product of two Vectors
Cross product is a binary operation (multiplication) that is performed on two vectors, and the resultant vector is perpendicular to both the given vectors. In this article, we will discuss cross product, right-hand thumb rule, properties of cross product and its implementation in python.
Vectors are the fundamental unit of linear algebra and are extensively used to describe machine learning algorithms, and we can perform algebraic operations over these vectors. In the previous article, we discussed one such operation, i.e., the dot product of vectors. This article will discuss another method of multiplication of vectors, i.e., cross-product of vectors.
Table of Content
Best-suited Data Science Basics courses for you
Learn Data Science Basics with these high-rated online courses
What is Cross Product
Definition
Cross product is a binary operation (multiplication) that is performed on two vectors, and the resultant vector is perpendicular to both the given vectors.
Dissimilar to the dot product, the result of the cross-product is a vector, i.e., it is also referred as a Vector Product.
Notation: If a and b are two vectors, then the cross-product is given by:
a x b.
Formula
- If a = a1 i + a2 j + a3 k, and b = b1 i + b2 j + b3 k, then
- If the angle between two vectors is given, then
where
|a| is the magnitude of a
|b| is the magnitude of b
theta: angle between a and b
n: unit vector at a right angle to both a and b
Note:
- The resultant vector of a x b is orthogonal (perpendicular) to both the vectors.
- Two non-zero vectors, a and b, are parallel if and only if a x b = 0
Example
- a = <1, 2, 3>, and b = <-1, -2, -3>. Find a x b.
Answer:
Here, a1 = 1, a2 = 2, a3 = 3, b1= -1, b2 = -2, and b3 = -3.
Now, substituting the value of a1, a2, a3, b1, b2, and b3 in the above-mentioned formula, we get
a x b = (a2b3 – a3b2)i – (a1b3 – a3b1)j + (a1b2 – a2b1)k
=> a x b = [(2)(-3) – (3)(-2)]i – [(1)(-3) – (3)(-1)]j + [(1)(-2) – (2)(-1)]k
=> a x b = [-6 + 6]i – [-3 + 3] j + [-2 + 2]k
=> a x b = 0
Hence, both the vector a and b are parallel to each other.
- If |a| = 1, |b| = 2, and the angle between both vectors is 30, then find a x b.
Answer:
Here, we have
| Programming Online Courses and Certification | Python Online Courses and Certifications |
| Data Science Online Courses and Certifications | Machine Learning Online Courses and Certifications |
Right-Hand Thumb Rule:
Until now, we clearly understand that the result of the cross product of two vectors is always perpendicular to both vectors. But how will you decide the direction of the resultant vector, i.e., whether it will point upward or downward?
The right-Hand Thumb Rule can resolve this problem.
It states, if:
Index finger: denotes the direction of vector a.
Middle finger: denotes the direction of vector b.
Then,
Thumb will denote the direction of a x b.
Properties of Cross Product
- If a, b, and c are three vectors, and k be any scalar, then
Non-Commutative: a x b = – a x b
Non-Associative: a x (b x c) != (a x b) x c
Distributive over addition
- a x (b + c) = a x b + a x c
- (a + b) x c = a x c + b x c
Dot Product: a (b x c) = (a x b) c
(ca) x b = c( a x b) = a x (cb)
a x (b x c) = (ac)b – (ab)c
- If i, j, and k are the components of the vectors, then:
i x j = k j x k = i k x i = j
j x i = -k k x j = -i i x k = -j
Till now, we have studied cross-product, their properties, right-hand thumb rule to find the directions, so I think that is enough to understand the cross-product. Isn’t it??
So, moving forward, we will see how to implement the cross-product in python with the help of an example.
Cross-Product of two vectors in Python
Method -1: Using Numpy
#cross-product of two vetcor using numpy import numpy as np # create vectorsa = [1, 2, 3]b = [ 4, 5, 6] #calculate the cross product of two vectors using np.cross(a,b) print("Cross-Product of a and b is: ", np.cross(a, b))
Output
Method -2: By defining a function
#cross-product by defining a function #if a = (a1, a2, a3), and b = (b1, b2, b3), then# a x b = [(a2b3 - a3b2)i - (a1b3 - a3b1)j + (a1b2 - a2b1)k] # create vectorsa = [1, 2, 3]b = [ 4, 5, 6] #define a function to calculate the cross-product def cross_prod(a, b): result = [a[1]*b[2] - a[2]*b[1], a[2]*b[0] - a[0]*b[2], a[0]*b[1] - a[1]*b[0]] return result #calculate cross-product print("Cross-Product of a and b is : ", cross_prod(a, b))
Output
Difference between Dot Product and Cross Product
| Cross-Product | Dot Product | |
| Definition | Product of magnitude of vectors and sin of the angle between them. | Product of the magnitude of vectors and cos of the angle between them. |
| Formula | |a||b|sin(theta) | |a||b|cos(theta) |
| Result | Resultant is a vector quantity. | Resultant is a scalar quantity. |
| Properties | Don’t satisfy commutative law. | Satisfies commutative law. |
| If two vectors are parallel, then the cross-product is zero. | If two vectors are perpendicular, then the dot product is zero. |
Conclusion
In this article, we have briefly discussed cross-product, right hand thumb rule, properties of cross-product, and implementation of cross-product in python.
Hope you will like the article.
Top Trending Article
Top Online Python Compiler | How to Check if a Python String is Palindrome | Feature Selection Technique | Conditional Statement in Python | How to Find Armstrong Number in Python | Data Types in Python | How to Find Second Occurrence of Sub-String in Python String | For Loop in Python |Prime Number | Inheritance in Python | Validating Password using Python Regex | Python List |Market Basket Analysis in Python | Python Dictionary | Python While Loop | Python Split Function | Rock Paper Scissor Game in Python | Python String | How to Generate Random Number in Python | Python Program to Check Leap Year | Slicing in Python
Interview Questions
Data Science Interview Questions | Machine Learning Interview Questions | Statistics Interview Question | Coding Interview Questions | SQL Interview Questions | SQL Query Interview Questions | Data Engineering Interview Questions | Data Structure Interview Questions | Database Interview Questions | Data Modeling Interview Questions | Deep Learning Interview Questions |
FAQs
What is a cross product?
Cross product is a binary operation (multiplication) that is performed on two vectors, and the resultant vector is perpendicular to both the given vectors.
What is Right Hand Thumb Rule?
Right hand thumb rule states if Index finger denotes the direction of vector a. Middle finger denotes the direction of vector b. Then, Thumb will denote the direction of a x b.
How Cross Product is different from Dot Product?
Dot product of two vectors is always a scalar, while the cross product of the two vectors will be a vector.
Vikram has a Postgraduate degree in Applied Mathematics, with a keen interest in Data Science and Machine Learning. He has experience of 2+ years in content creation in Mathematics, Statistics, Data Science, and Mac... Read Full Bio
Top Picks & New Arrivals
