Depth First Search Algorithm
Data structures like trees and graphs are traversed or explored by the depth-first search algorithm, or DFS. The algorithm starts at the root node (in the case of a graph, you can choose any random node as the root node) and analyses each branch as far as it can go before backtracking. This article will briefly discuss DFS and how it works.
The process of visiting each vertex (node) in a graph is known as graph traversal. A smaller graph is relatively simple to navigate. However, the process must be automated when navigating a graph with many nodes. Manual processes increase the likelihood of missing one or more vertices. And visiting nodes in a graph becomes crucial when you need to modify certain nodes, retrieve a value that was stored there, or do something else. Our graph traversing methods can help in this situation.
Two techniques exist for navigating a graph data structure:
- DFS, or the Depth-First Search algorithm
- BFS or the Breadth-First Search algorithm
Also Read: All you need to know about Data Structure and Algorithm
Also Read: Data Structures and Algorithms Online Courses & Certifications
Table of Content
Best-suited Data Structures and Algorithms courses for you
Learn Data Structures and Algorithms with these high-rated online courses
What is Depth First Search Algorithm (DFS)
Data structures like trees and graphs are traversed or explored by the depth-first search algorithm, or DFS. The algorithm starts at the root node (in the case of a graph, you can choose any random node as the root node) and analyses each branch as far as it can go before backtracking.
Also Read: What are Algorithms
Also Read: Bubble Sort Algorithm
How does the DFS algorithm work?
This is how the DFS algorithm operates:
- Start by keeping any vertex of the graph on top of the stack.
- Add the item at the top of the stack to the visited list.
- Make a list of the nodes that are close to that vertex. Place the items that haven’t been visited at the top of the stack.
- Repeat actions 2 and 3 until the stack is completely gone.
Also Read: Selection Sort Algorithm
Also Read: Quick Sort Algorithm
Traversal of all Vertices
Now that you have learned about the basics of depth-first search. Let’s see one of the basic use cases of DFS, which is traversing all vertices in a graph.
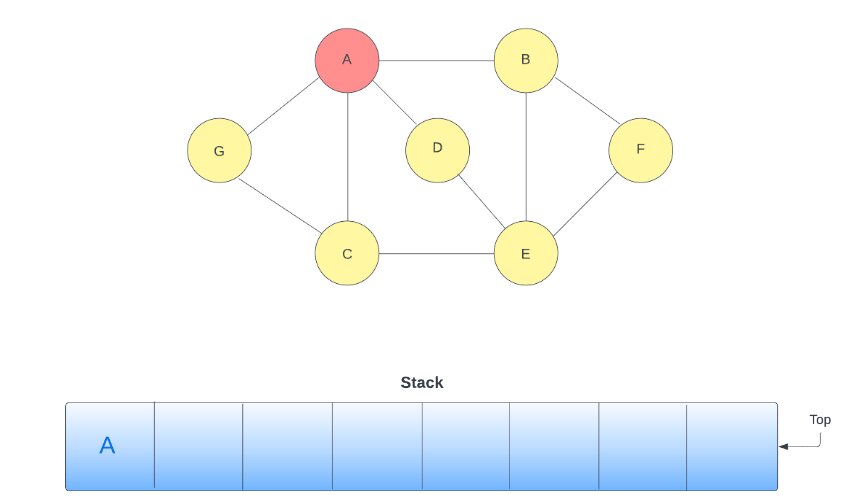
Consider an example graph given below:
Now the task is to start traversing this graph from node A and access each node using the DFS algorithm. We will cover it in the form of steps:
As mentioned above, we will use stack to complete our traversal.
Before proceeding, let’s have some assumptions throughout the process to keep the explanations simple.
- Each node is represented with a different color.
Also Read: Merge Sort Algorithm
Also Read: Insertion Sort Algorithm
Steps to traverse:
- Pick ‘A‘ and put it into the stack.
- Remove ‘A‘ from the stack and put its adjacent nodes (‘B‘, ‘D‘, ‘C‘, and ‘G‘) into the stack. Mark ‘A‘ visited (the visited nodes are represented in red color) and print it in output.
3. Consider the top element of the stack ‘G‘, remove it from the stack, and put the adjacent nodes of ‘G‘ (‘C‘ and ‘A‘) into the stack. Mark ‘G‘ as visited and print it in output.
4. The top of the stack is ‘A‘; remove ‘A‘ from the stack. Before traversing towards ‘A‘, check if this node is visited or not. Since ‘A‘ is already visited so you do not need to revisit it, and we can ignore it.
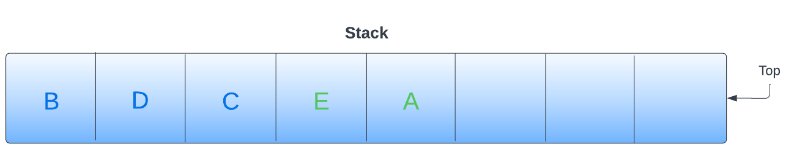
5. Pop ‘C‘ and check if it visited or not. Since ‘C‘ is not visited, add the adjacent node of ‘C‘ (‘E‘, ‘A‘, and ‘G‘) to the stack. Mark ‘C‘ as visited and print it in output.
6. The top of the stack is ‘G‘; remove ‘G‘ from the stack. Before traversing towards ‘G‘, check if this node is visited or not. Since ‘G‘ is already visited so, you do not need to revisit it, and we can ignore it.
7. Now the top of the stack is ‘A‘; remove ‘A‘ from the stack. Before traversing towards ‘A‘, check if this node is visited or not. Since ‘A‘ is already visited so, you do not need to revisit it, and we can ignore it. The stack looks like this.
8. Now come back to ‘C‘ and check if any edge is left; we have ‘E‘ left. Pop ‘E‘ and check if it visited or not. Since ‘E‘ is not visited, add the adjacent node of ‘E‘ (‘F‘, ‘B‘, ‘D‘, and ‘C‘) and add it to the stack. Mark ‘E‘ as visited and print it in output.
9. The top of the stack is ‘C‘; remove ‘C‘ from the stack. Before traversing towards ‘C‘, check if this node is visited or not. Since ‘C‘ is already visited so, you do not need to revisit it, and we can ignore it.
10. The top of the stack is ‘D‘; remove ‘D‘ from the stack. Pop ‘D‘ and check if visited or not. Since ‘D‘ is not visited, add the adjacent node of ‘D‘ (‘E‘ and ‘A‘) and add it to the stack. Mark ‘D‘ as visited and print it in output.
11. Now the top of the stack is ‘A‘; remove ‘A‘ from the stack. Before traversing towards ‘A‘, check if this node is visited or not. Since ‘A‘ is already visited so, you do not need to revisit it, and we can ignore it.
12. The top of the stack is ‘E‘; remove ‘E‘ from the stack. Before traversing towards ‘E‘, check if this node is visited or not. Since ‘E‘ is already visited so, you do not need to revisit it, and we can ignore it. The stack looks like this.
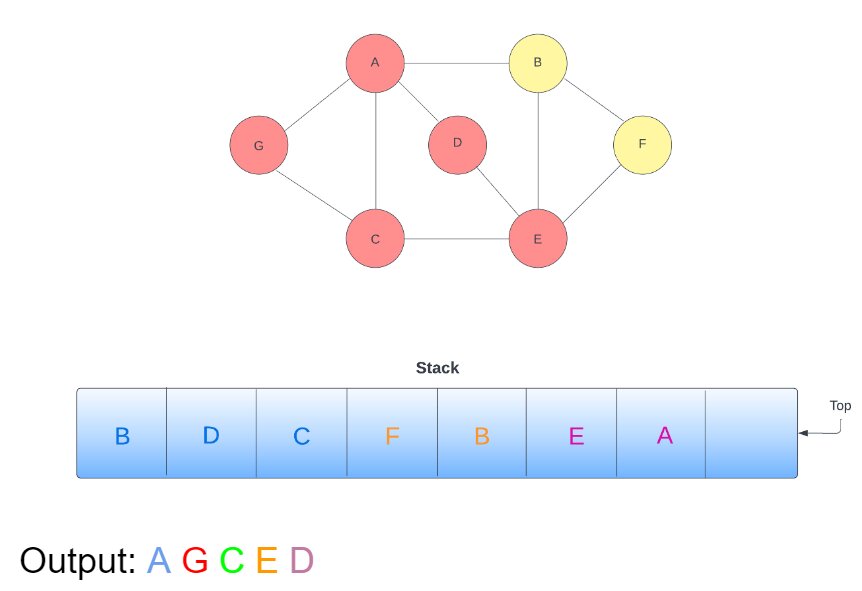
13. Now come back to ‘E‘ and check if any edge is left; we have ‘B‘ and ‘F‘ left, as seen in the stack. Pop ‘B‘ and check if it visited or not. Since ‘B‘ is not visited, add the adjacent node of ‘B‘ (‘F‘, ‘E‘, and ‘A‘) and add it to the stack. Mark ‘B‘ as visited and print it in output.
14. Now the top of the stack is ‘A‘; remove ‘A‘ from the stack. Before traversing towards ‘A‘, check if this node is visited or not. Since ‘A‘ is already visited so, you do not need to revisit it, and we can ignore it. The stack looks like this.
15. The top of the stack is ‘E‘; remove ‘E‘ from the stack. Before traversing towards ‘E‘, check if this node is visited or not. Since ‘E‘ is already visited so, you do not need to revisit it, and we can ignore it.
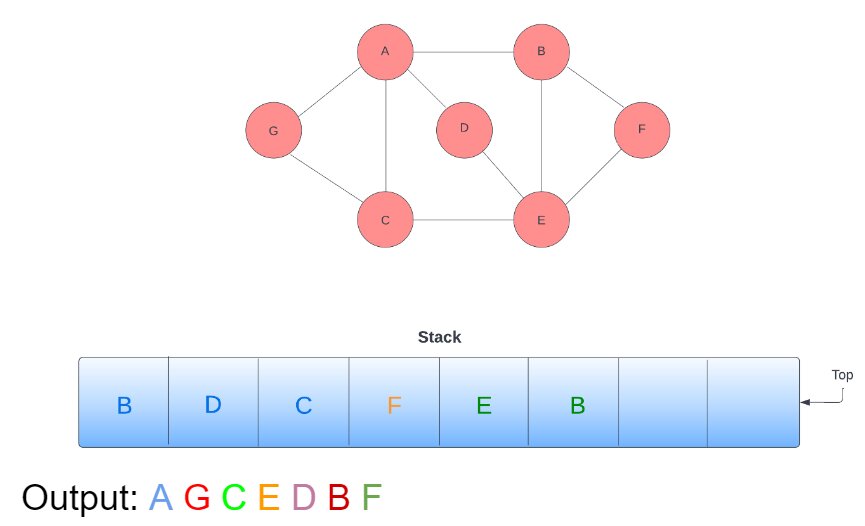
16. The top of the stack is ‘F‘; remove ‘F‘ from the stack. Pop ‘F‘ and check if it visited or not. Since ‘F‘ is not visited, add the adjacent node of ‘F‘ (‘E‘ and ‘B‘) and add it to the stack. Mark ‘F‘ as visited and print it in output.
17. Now the top of the stack is ‘B‘; remove ‘B‘ from the stack. Before traversing towards ‘B‘, check if this node is visited or not. Since ‘B‘ is already visited so, you do not need to revisit it, and we can ignore it.
18. The top of the stack is ‘E‘; remove ‘E‘ from the stack. Before traversing towards ‘E‘, check if this node is visited or not. Since ‘E‘ is already visited so, you do not need to revisit it, and we can ignore it.
19. All nodes present in the stack have been visited, you can check it in sequence, and at the end stack gets empty, and the final transversal output looks like this:
Pseudo Code
//Pseudo code for DFSDFS(adjacent[][], source, visited[], key) { if(source == key) return true //We found the key visited[source] = True FOR node in adjacent[source]: IF visited[node] == False: DFS(adjacent, node, visited) END IF END FOR return false // If it reaches here, then all nodes have been explored and we still havent found the key.}
Following is the java implementation of the DFS algorithm:
import java.io.*;import java.util.*; //Representing directed graph using adjacency// list representationclass Graph { private int V; // No. of vertices private LinkedList\n \n <integer>\n \n adjacency[];\n \n \n \n // Constructor\n \n Graph(int v)\n \n {\n \n V = v;\n \n adjacency = new LinkedList[v];\n \n for (int i = 0; i < v; ++i)\n \n adjacency[i] = new LinkedList();\n \n }\n \n \n \n // Function to add an edge into the graph\n \n void addEdge(int v, int w)\n \n {\n \n adjacency[v].add(w); // Add w to v's list.\n \n }\n \n \n \n // A function used by DFS\n \n void dfs(int v, boolean visited[])\n \n {\n \n // Mark the current node as visited and print it\n \n visited[v] = true;\n \n System.out.print(v + " ");\n \n \n \n // Recur for all the vertices adjacent to this\n \n // vertex\n \n Iterator\n \n \n \n <integer>\n \n i = adjacency[v].listIterator();\n \n while (i.hasNext()) {\n \n int n = i.next();\n \n if (!visited[n])\n \n dfs(n, visited);\n \n }\n \n }\n \n \n \n // The function to do DFS traversal. It uses recursive\n \n // dfs()\n \n void depthFirst()\n \n {\n \n // Mark all the vertices as not visited(set as\n \n // false by default in java)\n \n boolean visited[] = new boolean[V];\n \n \n \n // Call the recursive helper function to print DFS\n \n // traversal starting from all vertices one by one\n \n for (int i = 0; i < V; ++i)\n \n if (visited[i] == false)\n \n dfs(i, visited);\n \n }\n \n \n \n public static void main(String args[])\n \n {\n \n Graph grp = new Graph(4);\n \n \n \n grp.addEdge(0, 1);\n \n grp.addEdge(0, 2);\n \n grp.addEdge(1, 2);\n \n grp.addEdge(2, 3);\n \n grp.addEdge(3, 4);\n \n grp.addEdge(4, 1);\n \n \n \n // Function call\n \n grp.depthFirst();\n \n }\n \n }\n \n \n \n \n \n </integer>\n \n \n \n </integer>
Application of DFS Algorithm
The following uses for the DFS algorithm are listed:
- The topological sorting can be implemented using the DFS algorithm.
- It can be applied to determine the routes connecting two vertices.
- It can also be used to find graph cycles.
- DFS technique is also applied to puzzles with a single solution.
Also Read: All about Heap Sort Technique
Also Read: Divide and Conquer Algorithm
Conclusion
In this article, we have briefly discussed how Depth First Search Algorithm works and its application.
Hope you will like the article.
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio