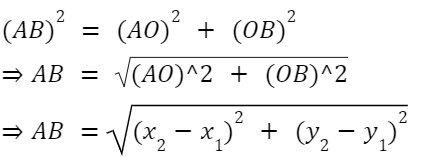How to Compute Euclidean Distance in Python
Euclidean Distance is one of the most used distance metrics in Machine Learning. In this article, we will discuss Euclidean Distance, how to derive formula, implementation in python and finally how it differs from Manhattan Distance.
Different machine learning algorithm, whether they are supervised or unsupervised, uses distance metrics to find the pattern in the input data. It helps to improve the performance of the machine learning models despite its classification or clustering tasks. Different distances metrics are available to calculate the distance between the input data, such as Manhattan Distance, Euclidean, Minkowski, and Hamming Distance. In the previous article, we discussed all about Manhattan Distance Metrics. This article will discuss the next distance metric, Euclidean Distance Metric.
Also Read: Evaluating a Machine Learning Algorithm
Also Read: Difference Between Supervised and Unsupervised Learning
So, let’s dive deep to learn more about Euclidean Distance Metric.
Table of Content
- What is Euclidean Distance
- Euclidean Distance Formula
- Euclidean Distance Python
- Difference between Euclidean Distance and Manhattan Distance
Best-suited Machine Learning courses for you
Learn Machine Learning with these high-rated online courses
What is Euclidean Distance
Euclidean Distance Metric is one of the most used distance metrics in the machine learning algorithm. It gives the shortest distance between two points.
The distance between two points in either the plane or 3-D space measures the length of the segment between two points.
- The distance between two points in either the plane or 3-D space measures the length of the segment between two points.
- They are generally used to calculate the distance between two rows of data that have numerical values (Integer or Decimal Values).
- KNN- classifier uses a Euclidean metric to classify the unknown instances by calculating the distance between the points in the training set.
- The value of the Euclidean distance will be greater than or equal to zero.
- If the value of the Euclidean Distance is Equal to zero, it implies that both the points are equivalent; else, they are different from each other.
Till now, we have learned about what is Euclidean distance metric and where it is used. Now, we will learn how to calculate the distance using it.
Euclidean Distance Formula
The Euclidean distance formula can be easily derived using the Pythagoras theorem.
Pythagoras’ Theorem states:
“In a right-angle triangle, the sum of the squares of the base and perpendicular is equal to the square of the hypotenuse.”
Now, we will calculate the Euclidean distance using the Pythagoras Formula:
Let’s take any two points (A, B) on a line segment that have coordinates A (x1, y1), and B (x2, y2), where (x1, x2) are the points on the x-axis and (y1, y2) are the points on y-axis.
Now, using these two points, draw a right-angle triangle, having the right angle at O, So the distance between
AO = (x2 – x1)
BO = (y2 – y1)
Now, using the Pythagoras Theorem, we will get the euclidean distance between two points (here AB), i.e.,
Hence, the euclidean distance between two points is:
The general formula of Euclidean Distance metric in n-dimension space is given by:
Where,
n: number of dimensions
(pi, qi): data points
| Programming Online Courses and Certification | Python Online Courses and Certifications |
| Data Science Online Courses and Certifications | Machine Learning Online Courses and Certifications |
Now, let’s have some examples to get a clear understanding of Euclidean Distance Metric:
Euclidean Distance Python
Here, we will discuss, two approaches to calculate the distance using python:
Method – 1: Using Dot and Square Root Method (Formula)
#using Formula# Import NumPy Libraryimport numpy as np
# initializing points in numpy arrays
P1 = np.array((9, 16, 25))P2 = np.array((1, 4, 9))
# subtracting both the vectors
temp = P1 - P2
# Using Formula
euclid_dist = np.sqrt(np.dot(temp.T, temp))
# printing Euclidean distanceprint(euclid_dist)
Output
21.540659
Method – 2: Using Sci-Py Library
# using distance.euclidean() method# Import SciPi Library
from scipy.spatial import distance# define the points
P1 = (9, 16, 25)P2 = (1, 4, 9)
# print Euclidean distance print(distance.euclidean(P1,P2))
Output
21.540659
Euclidean Distance vs. Manhattan Distance
| Parameter | Euclidean Distance | Manhattan Distance |
| Definition | It is the length of the line segment joining a given pair of points. | It is the sum of the distance at each point. |
| Uniqueness | It is unique and the shortest distance between two points. | There may be many Manhattan paths between two points. |
| Use | It is mainly used in the KNN algorithm. | It is used in Linear regression with Ridge Regularization. |
| Formula |  |
 |
Also Read: Lasso Regression vs Ridge Regression
Conclusion
Euclidean Distance is one of the most used distance metrics in Machine Learning. In this article, we will discuss Euclidean Distance, how to derive formula, implementation in python and finally how it differs from Manhattan Distance.
Hope this article helped you to learn more about Euclidean Distance.
Top Trending Article
Top Online Python Compiler | How to Check if a Python String is Palindrome | Feature Selection Technique | Conditional Statement in Python | How to Find Armstrong Number in Python | Data Types in Python | How to Find Second Occurrence of Sub-String in Python String | For Loop in Python |Prime Number | Inheritance in Python | Validating Password using Python Regex | Python List |Market Basket Analysis in Python | Python Dictionary | Python While Loop | Python Split Function | Rock Paper Scissor Game in Python | Python String | How to Generate Random Number in Python | Python Program to Check Leap Year | Slicing in Python
FAQs on How to Compute Euclidean Distance in Python
How can I compute the Euclidean distance between two points in 2D space using basic Python?
You can use the formula for Euclidean distance, which is the square root of the sum of the squared differences between corresponding coordinates.
import math
def euclidean_distance_2d(point1, point2):
return math.sqrt((point1[0] - point2[0])**2 + (point1[1] - point2[1])**2)
# Example usage
point1 = (1, 2)
point2 = (4, 6)
print(euclidean_distance_2d(point1, point2)) # Output: 5.0
How can I compute the Euclidean distance between two points in N-dimensional space using NumPy?
NumPy provides efficient array operations that can be used to compute the Euclidean distance.
import numpy as np
def euclidean_distance_numpy(point1, point2):
return np.linalg.norm(np.array(point1) - np.array(point2))
# Example usage
point1 = [1, 2, 3]
point2 = [4, 5, 6]
print(euclidean_distance_numpy(point1, point2)) # Output: 5.196152422706632
How can I compute the Euclidean distance between two points using the SciPy library?
from scipy.spatial.distance import euclidean
# Example usage
point1 = [1, 2, 3]
point2 = [4, 5, 6]
print(euclidean(point1, point2)) # Output: 5.196152422706632
How can I compute the Euclidean distance between two points using a custom function in Python?
def euclidean_distance_custom(point1, point2):
squared_diff = [(a - b) ** 2 for a, b in zip(point1, point2)]
return sum(squared_diff) ** 0.5
# Example usage
point1 = [1, 2, 3]
point2 = [4, 5, 6]
print(euclidean_distance_custom(point1, point2)) # Output: 5.196152422706632
How can I compute the Euclidean distance between multiple pairs of points in a dataset using Pandas?
Pandas can be used in combination with NumPy to compute the Euclidean distance for multiple pairs of points in a DataFrame.
import pandas as pd
import numpy as np
def euclidean_distance_pandas(df, point1_col, point2_col):
return np.linalg.norm(df[point1_col] - df[point2_col], axis=1)
# Example usage
data = {
'point1': [[1, 2], [3, 4]],
'point2': [[4, 6], [7, 8]]
}
df = pd.DataFrame(data)
df[['point1_x', 'point1_y']] = pd.DataFrame(df['point1'].tolist(), index=df.index)
df[['point2_x', 'point2_y']] = pd.DataFrame(df['point2'].tolist(), index=df.index)
print(euclidean_distance_pandas(df[['point1_x', 'point1_y']], df[['point2_x', 'point2_y']])) # Output: [5. 5.65685425]
Vikram has a Postgraduate degree in Applied Mathematics, with a keen interest in Data Science and Machine Learning. He has experience of 2+ years in content creation in Mathematics, Statistics, Data Science, and Mac... Read Full Bio
Top Picks & New Arrivals
