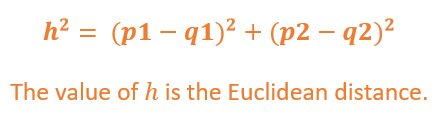K-means Clustering in Machine Learning
When you are dealing with Machine Learning problems that work with unlabeled training datasets, the most common learning algorithms you will come across are clustering algorithms. Amongst them, the simplest and the most popular is K-means clustering.
Typically, a good clustering algorithm groups the data into clusters such that the data points within each cluster are more similar to each other than the data points belonging to other clusters. Clustering algorithms find their usage in many applications including pattern detection, medical diagnosis, market segmentation, customer segmentation, etc. Let’s understand K-meanS Clustering in Machine Learning.
Explore Online Machine Learning Courses
In this blog, we will go through the following sections:
- What is K-means Clustering?
- How to Choose the value of K?
- How does the K-means algorithm work?
- Demo: Implementing K-means Clustering
- Assumptions of K-means
What is K-means Clustering?
K-means is a clustering algorithm designed to divide data points into distinct clusters depending on the similarities between the observations. Data points that share certain relevant characteristics are grouped together, implying that data points in different clusters would be dissimilar from each other.
This is an unsupervised learning algorithm, which means you can train a model to create clusters on some given data without needing to label it first.
Best-suited Machine Learning courses for you
Learn Machine Learning with these high-rated online courses
How to choose the value of K?
The number of clusters ‘K’ you want to group your data points into, has to be pre-defined. Determining the optimal number of clusters for a given data is a fundamental issue in K-means clustering. The answer to this question is somewhat subjective and mostly depends on the methods used for partitioning. The most commonly used method in the industry to identify the value of K is the elbow method.
The Elbow Method
In this method, the idea behind partitioning is to define clusters such that total intra-cluster variation or the total within the sum of squares (WSS) is minimized for each cluster. WSS measures the compactness of the clusters – so you’d want the value to be as small as possible.
The method consists of plotting the total WSS as a function of the various number of clusters. And then picking the ‘elbow’ of the curve as the appropriate number of clusters to use. See the example below.
The motive behind this method is the number of clusters should be chosen such that adding another cluster would not increase the total WSS.
The code to generate a graph and the modeling component of this algorithm is provided below in the Demo: Implementing K-means Clustering section of this blog.
How does the K-means algorithm work?
- Choose the value of K.
For example, let’s assume the value of K is 3.
- Select ‘K’ data points each of which represents a cluster centroid.
Since K=3, we will choose 3 random data points as centroids.
- Assign the rest of the data points to their nearest cluster centroids.
We will calculate the Euclidean distance between the data points and the centroids. The data point at a minimum distance with a given centroid is assigned to its cluster.
If we consider two points Pp1,p2 and Q(q1,q2) in a 2D space, the shortest distance between these two points is given as the length of the hypotenuse of a right triangle. This is the Euclidean distance between the two points.
The value of h is the Euclidean distance.
- Reposition the cluster centroid after each data point assignment till it’s the average of all data points in that cluster.
Once a data point is assigned to the nearest cluster, the cluster centroid is re-calculated, including the new point.
- Repeat steps 3 and 4 till there are no more changes in each cluster.
After the final iteration, this is how the clusters are formed:
K Means Clustering Demo in Python – Try it yourself
Click the below colab icon to run and practice the demo.
Demo: Implementing K-means Clustering – Explanation
Problem Statement:
We will demonstrate how to implement K-means clustering on a given dataset. We will determine the value of K using the Elbow Method we have studied above.
Please keep in mind that K-means clustering is not performed on categorical data.
Dataset Description:
We will be creating a dataset using the make_blobs API from the Scikit-learn library. This API is used to create multi-class datasets by allocating each class to one or more normally distributed clusters.
Tasks to be performed:
- Generate the data
- Visualize the data clusters
- Plot the Elbow Curve
- Build and Visualize the K-means Clustering Model
Step 1 – Generate the data
Let us generate a dataset with, say, 12 random clusters in a 2D space. For that, we will initialize this AdaBoost ensemble model with the following parameters:
- n_samples = 1000 – Create 1000 samples
- n_features = 2 – The dataset will have two features
- centers = 12 – Create 12 random clusters with 12 centroids
import pandas as pdfrom sklearn.datasets import make_blobs #Generate the dataX, y = make_blobs(n_samples=1000, n_features=2, centers=12, random_state=42) #Create a DataFrame for the dataset featuresdf = pd.DataFrame(X, columns=['feature1','feature2'])
Step 2 – Visualize the data clusters
We will use a Seaborn scatter plot to visualize our data with its 2 features:
import seaborn as sns import matplotlib.pyplot as plt #Create a scatter plot using seabornfig = plt.figure (figsize=(10,6))sns.scatterplot(x='feature1', y='feature2', data=df)
Though we specified 12 centers, the plot above shows an overlap between some clusters. So, have only 7-8 separable clusters right now.
Step 3 – Plot the Elbow Curve
We will use the Yellowbrick library, which is a wrapper around Scikit-learn. This library will help us plot the Elbow curve with only one line of code:
from yellowbrick.cluster import KElbowVisualizer
model = KMeans() #K is the range of number of clustersvisualizer = KElbowVisualizer(model, k=(2,18), timings=False) visualizer.fit(X) #Fit the data to the visualizervisualizer.show() #Display the figure
We found that the optimal value of the number of clusters using the Elbow Method is 6. Let’s see how our model clusters the data when K=6.
Step 4 – Build and visualize the K-means Clustering Model
Let’s see how our model clusters the data when K=6:
from sklearn.cluster import KMeans
#Create the model model = KMeans(n_clusters=6)
#Fit values to the model model.fit(X) #Predict the output labels df['y_pred'] = model.predict(X)
#Convert the output column to category df['y_pred'] = df['y_pred'].astype('category')
#Plot the clusterd data using seaborn fig = plt.figure (figsize=(10,6)) sns.scatterplot(x='feature1', y='feature2', hue='y_pred', data=df)
Thus, we have a perfectly grouped data divided into 6 defined clusters.


Assumptions of K-means Clustering
Like most machine learning models, K-means clustering also holds certain assumptions about the data they fit on. It is important to check on these assumptions before we rely on our trained model:
- K-means cannot handle non-globular structure
A given data can have any type or number of patterns that can be interpreted visually. Since the K-means algorithm uses centroids as a reference, it does not capture the information well if the data has a non-globular pattern.
- K-means is susceptible to outliers.
We already know that in K-means, centroids are re-calculated repeatedly by averaging the data points in the cluster. Averages are sensitive to outliers. So, it becomes necessary to spot and remove outliers before training our model.
Endnotes
K-means clustering is a powerful and extensively used technique for data cluster analysis in Machine Learning. The only tough part of the algorithm is identifying an ideal value of K. However, due to its limitations, its performance might not be the best among other clustering techniques because the slightest variations in the data could lead to a high variance error.
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio