Model Selection in Machine Learning: Regression
Selecting the correct model to match your data is a crucial stage in the regression analysis process. For accurate and insightful findings, the proper model must be chosen because different models may fit the data differently and produce different predictions. The procedure for selecting a model for regression analysis will be covered in this article, along with advice on how to select the most appropriate model for your set of data with the help of some of the validation techniques.
Through this article on model selection in machine learning, we will be discussing the details for model selection via regression analysis.
Table of Contents
- What is regression analysis?
- Types of regression analysis
- Stages of model selection in machine learning: Regression
- Ensemble Method
- Random Method
- Gradient Boosting Method
- Comparison
- Model Evaluation
What is Regression Analysis?
Regression analysis refers to the statistical method for determining how one or more independent variables and a dependent variable are related. Building a model that can forecast the value of dependent variable based on values of independent variables is the aim of regression analysis. The model may include one or more independent variables and may be linear or nonlinear.
Best-suited Machine Learning courses for you
Learn Machine Learning with these high-rated online courses
Type of Regression
The following are different types of regression:
- Linear regression: When there is a linear relationship between the dependent and independent variables, linear regression—the simplest type of regression—is performed. In order to minimise the total of the squared discrepancies between the observed and predicted values, a straight line will be fitted to the data in this model. In forecasting and trend analysis, linear regression is frequently utilised.
- Multiple regression: When there are several independent variables that are connected to the dependent variable, multiple regression is performed. Finding a linear relationship between the dependent and independent variables is the goal. When using multiple regression, the model maintains the same values for all other independent variables while estimating the impact of each independent variable.
- Logistic regression: When a dependent variable is binary (for example, 0 or 1, yes or no), and the independent variables are continuous or categorical, logistic regression is utilised. Estimating the likelihood that the dependent variable falls into one of the two categories is the goal. Predictive modelling frequently employs logistic regression, which is utilised in a variety of industries like marketing, banking, and healthcare.
- Polynomial regression: When there is a nonlinear relationship between dependent and independent variables, polynomial regression is performed. In this model, the data are fit to a polynomial function, allowing for more intricate interactions between the dependent and independent variables. Physics and engineering both frequently use polynomial regression.
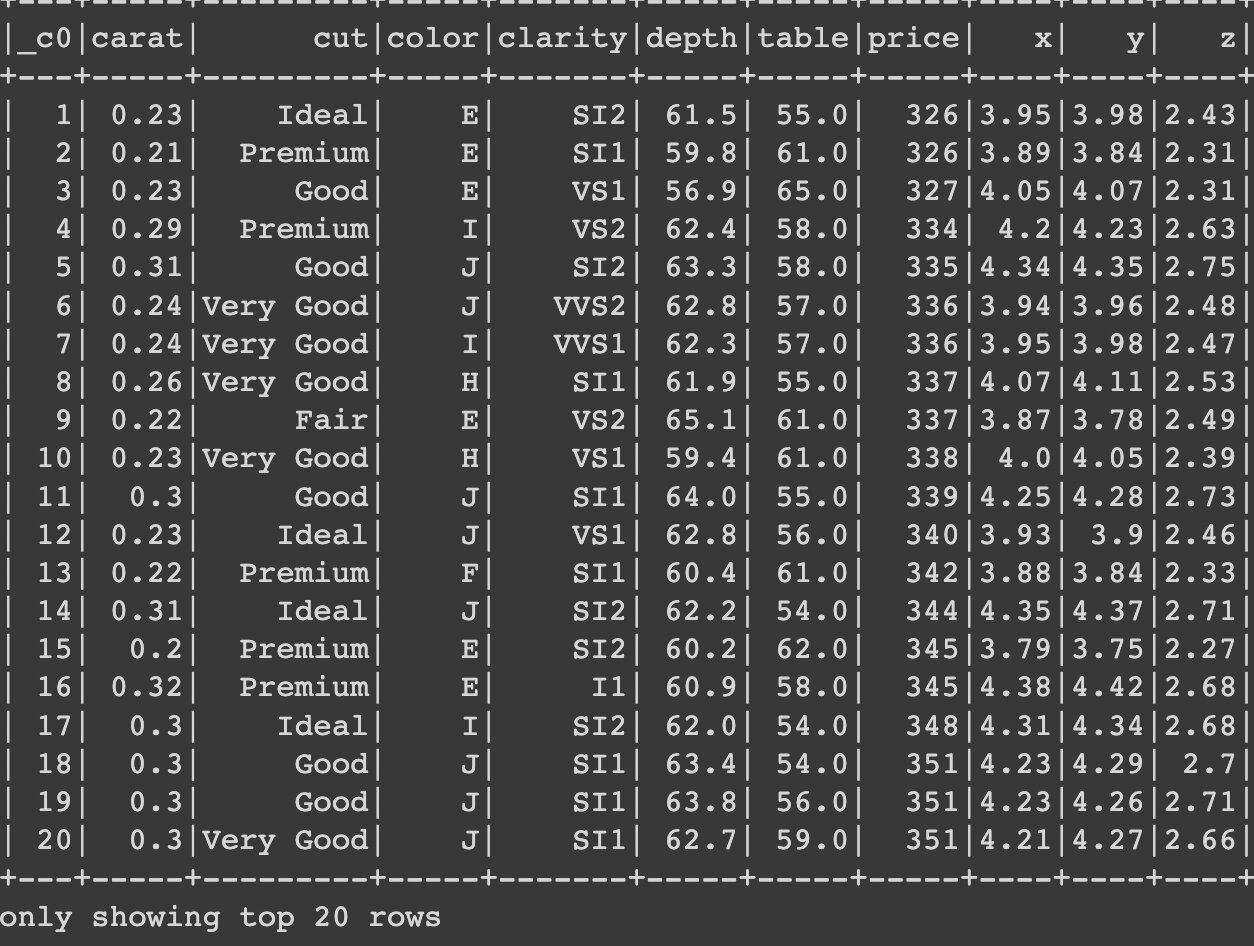
The below-given image shows the types of regression models.
The example dataset shown above is used for a linear regression model. It displays the first 20 rows and columns of the dataset, which is used to predict the price of diamonds. In addition to linear regression, some ensemble models are also employed to analyze this dataset.
Stages of Model Selection in Machine Learning
The following stages are encountered while choosing a model:
Stage 1: Selecting the regression model forms
Choosing the right kind of regression model to utilise is the first stage in the model selection process. Regression models come in a variety of forms, such as logistic regression, polynomial regression, and linear regression. The type of data being used and the research question being addressed influence the model selection. For instance, logistic regression is utilised for binary outcomes while linear regression is suitable for continuous data.
To choose the appropriate model for a given dataset, it is crucial to analyze and understand the characteristics of the data. In the example above dataset, the target variable shows a continuous dependent variable, indicating that models such as linear regression, random forest, and decision tree can be used for analysis.
Stage: 2 Selecting the regression model and the independent variables
The next step is to choose the proper sort of regression model and then the independent variables that will be included in the model. This is frequently accomplished using exploratory data analysis and feature selection process which entails analysing the correlation between each prospective predictor variable and the dependent variable. The dependent variable is chosen for inclusion in the model together with other variables that seem to have a significant link with it.
Example: We are going to predict the price of the diamond with the dataset, so the independent variable(x) is the price.
Stage: 3 Fitting the model
Fitting the regression model to the data comes next after choosing the independent variables. Estimating the values of the model parameters (coefficients) that best describe the relationship between the dependent variable and the independent variables is the aim of model fitting. Most often, the least squares estimate is used for this, which reduces the sum of squared errors between the dependent variable’s observed values and the model’s predicted values.
Stage: 4 Examining or validation of the applied model
The next stage is to assess the regression model’s performance after the data have been fitted to the model. Examining the goodness of fit, which gauges how well the model fits the data, is one approach to do this. The coefficient of determination (R-squared), which calculates how much of the variance in the dependent variable is explained by the independent variables, is the most widely used indicator of how well a model fits its data.
R-squared is a valuable indicator of goodness of fit, but it is not enough to choose a model. This is because, even if new independent variables do not enhance the model’s predictive ability, their addition will always result in a higher R-squared. As a result, it’s crucial to assess the model’s performance using other techniques and select the best model.
The image shows how to calculate the R Square value
To make sure a model is precise, dependable, and generalizable to new data, it must be validated and evaluated. Before the model is used to make decisions, it aids in identifying potential problems with it and enables changes.
Ensemble Method
The image shows the procedure which decision tree uses to select a best model
Using decision trees or ensemble approaches like Random Forest or Gradient Boosting are additional methods for model selection. A non-parametric method called decision trees divides the data into subsets recursively according to the values of the predictors. Multiple decision trees are combined using ensemble methods to increase the model’s precision and generalizability.
When dealing with relationships between the predictors and the response variable that are not linear, decision trees and ensemble approaches can be especially helpful. Decision trees can capture intricate relationships between the predictors and the response variable by recursively partitioning the data into subsets. Through the combination of several trees and the elimination of overfitting, ensemble approaches can enhance the performance of decision trees even more.
Cross-validation can be used to fine-tune the parameters of the ensemble approach, such as the ideal number of trees or the hyperparameters. For instance, the number of trees and predictors to take into account at each split are hyperparameters in Random Forest. The ideal ensemble model can be discovered by choosing the values of these hyperparameters that minimise the cross-validation error.
While decision trees and ensemble approaches can be effective tools for model selection, it’s crucial to keep in mind that they can also be overfitting-prone and challenging to interpret. It is crucial to thoroughly assess the performance and interpretability of the chosen model and to combine these methods with other model selection strategies.
When selecting the optimal model for your data, there are a number of other factors to take into account in addition to these strategies. The regression model’s assumptions are one crucial factor. Most regression models make the assumption that the connection between the predictors and the response variable is linear, the mistakes are normally distributed, and the variance of the errors is constant. In the event that these presumptions are broken, the model may not produce reliable or insightful results.
Example:
Python code:
# RMSElr_rmse = RegressionEvaluator(predictionCol="prediction", labelCol="log_price", metricName="rmse").evaluate(lr_predictions)print('Linear Regression Model - RMSE: {:.2f}'.format(lr_rmse))
# MSE lr_mse = RegressionEvaluator(predictionCol="prediction", labelCol="log_price", metricName="mse").evaluate(lr_predictions)print('Linear Regression Model - MSE: {:.2f}'.format(lr_mse))
# MAPElr_mape = lr_predictions.select((abs(col('log_price') - col('prediction'))/col('log_price')).alias('mape')).agg(avg(col('mape')).alias('mape')).collect()[0]['mape'] * 100print('Linear Regression Model - MAPE: {:.2f}%'.format(lr_mape))
# MAElr_mae = RegressionEvaluator(predictionCol="prediction", labelCol="log_price", metricName="mae").evaluate(lr_predictions)print('Linear Regression Model - MAE: {:.2f}'.format(lr_mae))
Output:
Linear Regression Model - RMSE: 0.37Linear Regression Model - MSE: 0.14Linear Regression Model - MAPE: 3.98%Linear Regression Model - MAE: 0.30
Advantages of Ensemble methods
- Improved Accuracy: Ensemble approaches combine the predictions of various models, each of which may have its own advantages and disadvantages, to increase the accuracy of a model.
- Robustness: Because the pooled predictions can smooth out errors and inconsistencies, ensemble approaches are less prone to overfitting and inaccuracies in individual models.
- Diversity: Ensemble approaches can include diverse models with various architectures, algorithms, and hyperparameters, which can enhance the model’s generalisation capabilities.
- Scalability: Because ensemble methods may parallelize the training and evaluation of numerous models, they can be employed with big datasets and complex models.
Disadvantages of Ensemble methods
- Increased Complexity: Due to the need for additional training and evaluation procedures as well as techniques for aggregating the predictions of various models, ensemble approaches might be more complex than individual models.
- Sensitivity to Input Data: Because the models may behave differently on various subsets of the data and because the technique for combining the predictions may also depend on the data, ensemble methods may be sensitive to the quality and distribution of the input data.
- Computationally Intensive: Due to the need to train and test several models, ensemble approaches can be computationally demanding, especially for big datasets or complicated models.
- Interpretability: Since ensemble approaches combine the predictions of various models, it may be more challenging to comprehend the underlying patterns and relationships in the data. As a result, ensemble methods may be less interpretable than individual models.
Random Forest
A well-liked ensemble learning technique called random forest can be applied to both classification and regression applications. A random forest model in regression consists of several decision trees, each of which was trained using a random subset of the input features and training samples.
The steps for creating a random forest regression model are as follows:
- Data preparation: Cleanse, preprocess, and divide the data into training and testing sets.
- Build Trees: Using a random subset of the input features and training samples, build a lot of decision trees. Using a series of splitting rules that divide the data into smaller subgroups based on the input attributes, each tree is trained to predict the target variable.
- Ensemble trees: These trees combine their individual forecasts to make a single prediction. Averaging the results of the individual trees is the strategy used most frequently to combine the forecasts.
- Model Evaluation: Use relevant measures, such as mean squared error (MSE), mean absolute error (MAE), or R-squared (R2), to assess the effectiveness of the random forest regression model.
Example
Python code:
# calculate the RMSE, MSE, MAE, and MAPE for the Random Forest Regression modeldt_evaluator = RegressionEvaluator(predictionCol='prediction', labelCol='log_price', metricName='mse')dt_mse = dt_evaluator.evaluate(dt_predictions)dt_evaluator.setMetricName('rmse')dt_rmse = dt_evaluator.evaluate(dt_predictions)
dt_mape = dt_predictions.select((abs(col('log_price') - col('prediction'))/col('log_price')).alias('mape')).agg(avg(col('mape')).alias('mape')).collect()[0]['mape'] * 100
dt_evaluator.setMetricName('mae')dt_mae = dt_evaluator.evaluate(dt_predictions)
Output:
Random Forest Regression Model - MSE: 0.055Random Forest Regression Model - RMSE: 0.234Random Forest Regression Model - MAE: 0.185Random Forest Regression Model - MAPE: 2.45%
Advantages
The following are some benefits of applying random forest to regression:
- Robustness: Because the pooled predictions can smooth out errors and inconsistencies, random forest regression is less prone to overfitting and inaccuracies in individual models.
- Non-linear Relationships: By modelling non-linear relationships between the input characteristics and the target variable, random forest regression can increase the model’s precision.
- Feature selection: The value of each input feature in predicting the target variable can be estimated via random forest regression, which is helpful for feature selection and interpretation.
Disadvantages
Nevertheless, there are some drawbacks to using random forest regression, including:
- Interpretability: Because random forest regression combines the predictions of several models, it can be more challenging to comprehend the underlying patterns and relationships in the data than individual decision trees.
- Overfitting: If the number of trees is too great or the model is not properly calibrated, random forest regression may still overfit the data.
Gradient Boosting Model
A common machine learning method for regression analysis called gradient boosting involves iteratively adding weak models to an ensemble in order to raise the performance of predictions in general. The technique is a subclass of boosting algorithm that, in each iteration, optimises the parameters of the weak models with the goal of reducing the loss function of the model.
The steps for creating a gradient boosting regression model are as follows:
- Data preparation: Cleanse, preprocess, and divide the data into training and testing sets.
- Initialise Model: Fit the gradient boosting model to the training data using a weak learner, such as a decision tree.
- Ensemble models: To make a final prediction, combine the unique predictions of each model in the ensemble. The most typical way to combine the forecasts is to add up the results from the various models.
- Model Evaluation: Use relevant metrics, such as mean squared error (MSE), mean absolute error (MAE), or R-squared (R2), to assess the gradient boosting regression model’s performance.
Explore machine learning courses
Example:
Python code:
# calculate the RMSE, MSE, MAE, and MAPE for the Gradient Boosted Trees Regression modelgbt_evaluator = RegressionEvaluator(predictionCol='prediction', labelCol='log_price', metricName='mse')gbt_mse = gbt_evaluator.evaluate(gbt_predictions)gbt_evaluator.setMetricName('rmse')gbt_rmse = gbt_evaluator.evaluate(gbt_predictions)
gbt_mape = gbt_predictions.select((abs(col('log_price') - col('prediction'))/col('log_price')).alias('mape')).agg(avg(col('mape')).alias('mape')).collect()[0]['mape'] * 100
gbt_evaluator.setMetricName('mae')gbt_mae = gbt_evaluator.evaluate(gbt_predictions)
# print the evaluation metricsprint('Gradient Boosted Trees Regression Model - MSE: {:.3f}'.format(gbt_mse))print('Gradient Boosted Trees Regression Model - RMSE: {:.3f}'.format(gbt_rmse))print('Gradient Boosted Trees Regression Model - MAE: {:.3f}'.format(gbt_mae))print('Gradient Boosted Trees Regression Model - MAPE: {:.2f}%'.format(gbt_mape))
Output:
Gradient Boosted Trees Regression Model - MSE: 0.053Gradient Boosted Trees Regression Model - RMSE: 0.229Gradient Boosted Trees Regression Model - MAE: 0.181Gradient Boosted Trees Regression Model - MAPE: 2.40%
Advantages
Using gradient boosting for regression analysis has the following benefits:
- Relationships that are not linear can be modelled using gradient boosting, which can increase the model’s accuracy by simulating non-linear relationships between the input data and the target variable.
- Since pooled predictions can smooth out flaws and inconsistencies, gradient boosting is less prone to overfitting and inaccuracies in individual models.
- Gradient boosting can estimate each input feature’s contribution to the prediction of the target variable, which is helpful for feature selection and interpretation.
Disadvantages
However, utilising gradient boosting for regression analysis has significant drawbacks as well, such as:
- Gradient boosting includes iteratively optimising the loss function and including weak learners in the ensemble, which can be computationally demanding, particularly for big datasets or complicated models.
- Gradient boosting can still overfit the data if the model is not calibrated properly or if there are too many weak learners.
Comparison of All Three Ensemble Models
Python code:
# create a dictionary with the evaluation metricsmetrics = { 'Model': ['Linear Regression', 'Decision Tree Regression', 'Random Forest Regression', 'GBTRegressor'], 'RMSE': [lr_rmse, dt_rmse, rf_rmse, gbt_rmse], 'MSE': [lr_mse, dt_mse, rf_mse, gbt_mse], 'MAE': [lr_mae, dt_mae, rf_mae, gbt_mae], 'MAPE': [lr_mape, dt_mape, rf_mape, gbt_mape]}
# create a Pandas DataFrame from the dictionarymetrics_df = pd.DataFrame(metrics)
# set the 'Model' column as the indexmetrics_df.set_index('Model', inplace=True)
# display the DataFrameprint(metrics_df)
Output:
RMSE MSE MAE MAPE
Model
Linear Regression 0.367998 0.135422 0.296465 3.976911
Decision Tree Regression 0.233621 0.054579 0.185308 2.453324
Random Forest Regression 0.233162 0.054364 0.184536 2.445240
GBTRegressor 0.229379 0.052615 0.181164 2.398151
Model Evaluation
A model can be evaluated and validated using a variety of techniques, such as:
1. Diagnostic Plots:
Diagnostic plots make the model’s fit easier to understand and help you spot any trends in the residuals. The discrepancies between the expected and actual values are known as residuals. Residual plots, QQ plots, and leverage plots are examples of typical diagnostic plots.
Residual analysis:
Residual analysis should satisfy three assumption
- The frequency of the residual should be normally distributed
- Homoscedasticity
- Independent
Example:
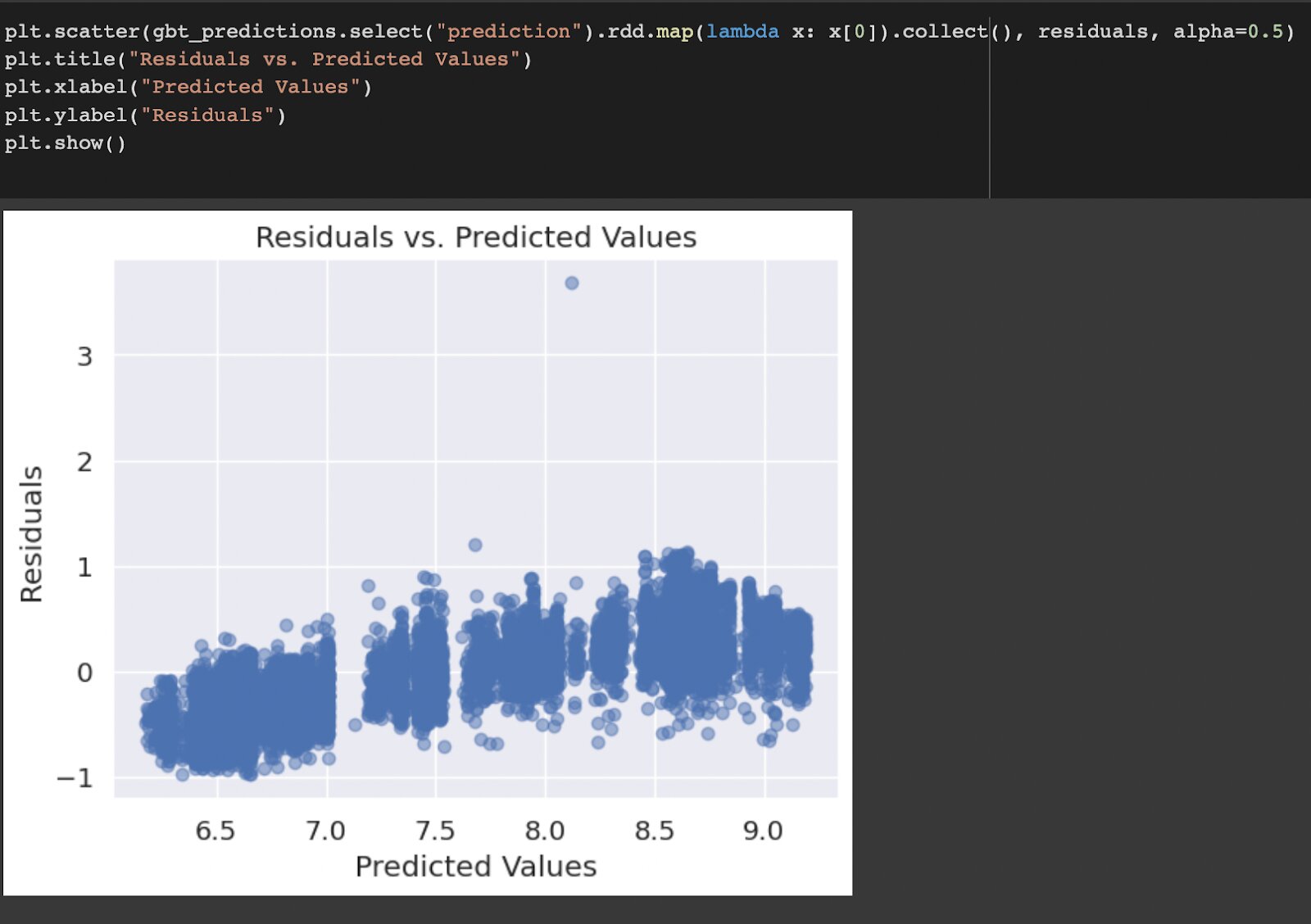
For Gradient boosting model:
In the above graph we can see that the frequency of the residual values are normally distributed.
In the above graph, the other two assumptions are also satisfied. There should not be any pattern in the graph. If we find any pattern in the graph, then the model’s performance is poor.
2. Goodness-of-fit:
- RMSE is a measure of the average distance between the predicted values and the actual values, calculated by taking the square root of the mean squared error. It is a commonly used metric for regression models because it emphasizes large errors and is easy to interpret in the units of the target variable.
- MSE is a measure of the average squared distance between the predicted values and the actual values. It is calculated by taking the average of the squared differences between the predicted and actual values. It is also commonly used in regression models because it emphasizes larger errors, but it is not as easy to interpret as RMSE because it is in squared units.
- MAE is a measure of the average absolute difference between the predicted values and the actual values. It is calculated by taking the average of the absolute differences between the predicted and actual values. It is useful because it is easy to interpret in the units of the target variable.
- MAPE is a measure of the average percentage difference between the predicted values and the actual values. It is calculated by taking the average of the absolute percentage differences between the predicted and actual values. It is useful for comparing the performance of models across different datasets or target variable scales, but it can be problematic when the actual values are close to zero.
As we have already found the value of RMSE, MSE, MAPE, and MAE. The value of RMSE and MSE should be close to 0 and MAPE value should be close to 0%.. By comparing all the three model used, the gradient boosting model’s performance is better.
Summary
- To sum up, model selection is a crucial stage in regression analysis that entails selecting the top model from a list of contenders that can precisely predict the response variable. Linear regression, Decision trees, and ensemble approaches are a few of the model selection strategies. Each technique has advantages and disadvantages, and the best one to use will depend on the nature of the data and the objectives of the research.
- Although it is a crucial phase in the regression analysis process, model selection is not the sole step. Once a model has been chosen, it is crucial to assess its performance on a different test set and validate the findings using further information. Additionally, it’s crucial to convey the study’s findings in a straightforward and intelligible way, especially if the model will be applied to make decisions.
- In conclusion, selecting the best model from a group of potential models is an important stage in the regression analysis process. There are numerous model selection strategies, each having advantages and disadvantages. When choosing a model, it’s crucial to take the regression model’s underlying assumptions into account, examine the diagnostic charts, and strike a balance between the model’s accuracy and interpretability. Choosing a model that correctly predicts the response variable and offers an understanding of the underlying links between the predictors and the response variable is the ultimate goal of the model selection process.
Contributed by: Vishwa Kiran
This is a collection of insightful articles from domain experts in the fields of Cloud Computing, DevOps, AWS, Data Science, Machine Learning, AI, and Natural Language Processing. The range of topics caters to upski... Read Full Bio