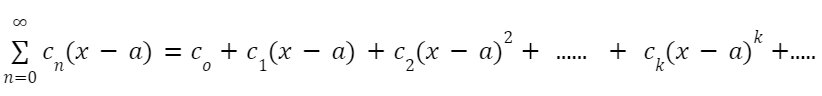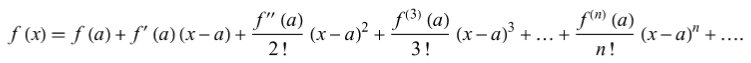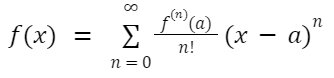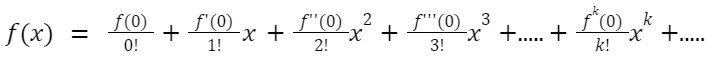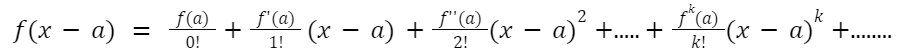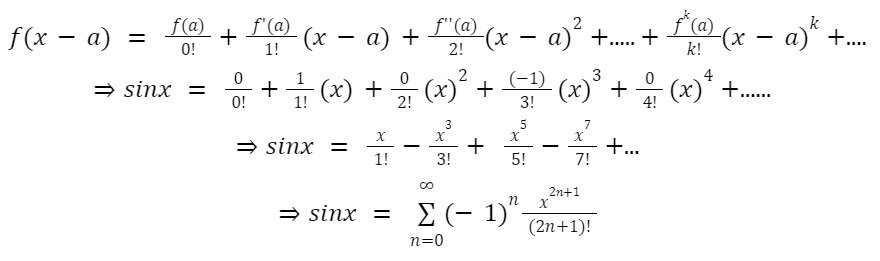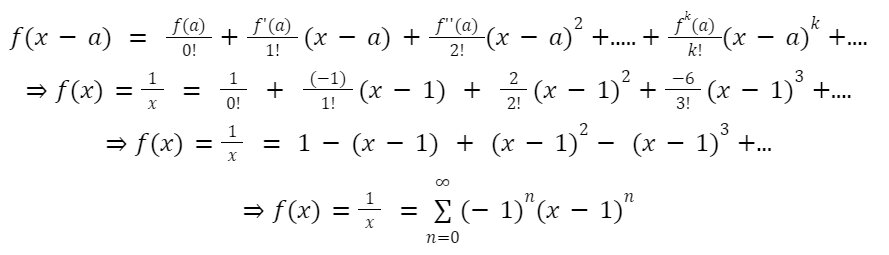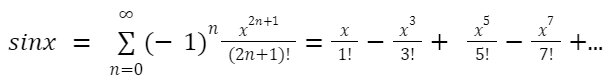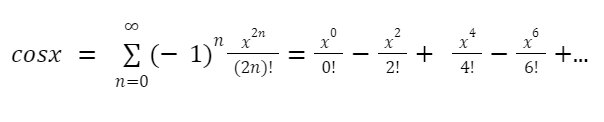Taylor Series Approximation: Definition, Formula, and Example

Let f(x) be a continuous and infinitely differentiable function (i.e., a function that can be differentiated infinite times), then the taylor series of f(x) is a series expansion of f(x) about a point x = a. In this article, we will discuss how to find the approximation of a function using the Taylor series.

Taylor series is a series expansion of a function around a point that can be utilized to approximate a function. It is an application of derivatives of a function that has a vast application in machine learning and deep learning.
In machine learning, to calculate the gradient descent, we try to minimize the cost function using differentiation. However, not all the functions can be differentiated, so here, we use the Taylor series to approximate the function.
Taylor series expansion is applied in the deep neural network to optimize the performance measure and is one of the most important uses of the Taylor series in deep learning.
In Neural Networks, the Taylor series can be applied to isolate the difficulties like shattered gradients. It can also be used to explain the neural network’s prediction quantitatively.
In this article, we will briefly discuss the Taylor series, its formula, its proof, and some of the common Taylor series expansions.

Table of Content

• What is the Taylor Series
  • Proof of Taylor Series Formula
  • Example
• Commonly used Taylor Series
  • Exponential Function
  • Logarithmic Function
  • Trigonometric Function
    • sin(x)
    • cos(x)
    • tan(x)

Before starting the taylor series, let’s discuss one important series that we will use to prove the taylor series formula, i.e., Power Series.

Power Series: Power series about the centre x = a is an infinite sum of the form

where

c_i: constant coefficients

What is the Taylor Series?

Let f(x) be a continuous and infinitely differentiable function (i.e., a function that can be differentiated infinite times), then the taylor series of f(x) is a series expansion of f(x) about a point x = a.

The Taylor series expansion of any function f(x) at x = a is given by:

This can also be written as:

Note: If in the above formula, a = 0, then the above expansion is known as Maclaurin Series.

What is Programming	What is Python
What is Data Science	What is Machine Learning

Proof of Taylor’s Theorem

Let f(x) be a polynomial function such that:

f(x) = a₀ + a₁x + a₂x² + a₃ x³ + a₄x⁴ +….. + a_k x^k+……,         ……. (1)

Now substituting x = 0, in (1), we get:

f(0) = a₀

=> a₀ = f(0)/0! …..(i)

Differentiating f(x), with respect to y, we get:

f’(x) = a₁ + 2a₂x + 3a₃x² + 4a₄x³ + ….,    …….(2)

Substituting x = 0, in (2) we get:

f’(0) = a₁

=> a₁ = f’(0)/1! …..(ii)

Differnetitaing f’(x), with respect to x we get:

f’’(x) = 2a₂ + 6 a₃ x + 12a₄ x² + ….,      …..(3)

Substituting x = 0 in equation (3), we get:

f’’(0) = 2a₂

=> a₂ = f’’(0)/ 2

=> a₂ = f’’(0)/ 2!….(iii)

Differentiating f’(y), with respect to y we get:

f’’’(x) = 6a₃ + 24a₄ x + ….., …………(4)

Substituting x = 0 in equation (4), we get:

f’’’(0) = 6a₃

=> a_3 = f’’’(0)/ 6 

=> a₃ = f’’’(0)/ 3!…..(iv)

Generalizing, the result of (i), (ii), (iii), and (iv) we get:

a_n = fⁿ(0) /n!……(v)
Now, substituting the value of (i), (ii), (iii), (iv), and (v) in (1), we get:

Now, generalizing the above we get:

Example

Example -1: Find the Taylor series of sin x for x = 0.

Answer: Here, f(x) = sin x, and we know sin x is an infinitely differentiable function that can be represented as:

Now, differentiating f(x), we get

f(x) = sin x => f(0) = 0

f’(x) = cos x => f’(0) = 1

f’’(x) = -sin x => f’’(0) = 0

f’’’(x) = -cos x => f’’’(0) = -1

f^(iv) (x) = sin x => f^(iv)(0) = 0

=> f^(iv)(x) = f(x)

So, continuing the differentiation we will get the repetition only

Now, substituting the above values in the Taylor series formula, we get:

Example – 2: Find the Taylor series expansion of f(x) = 1/x at x = 1.

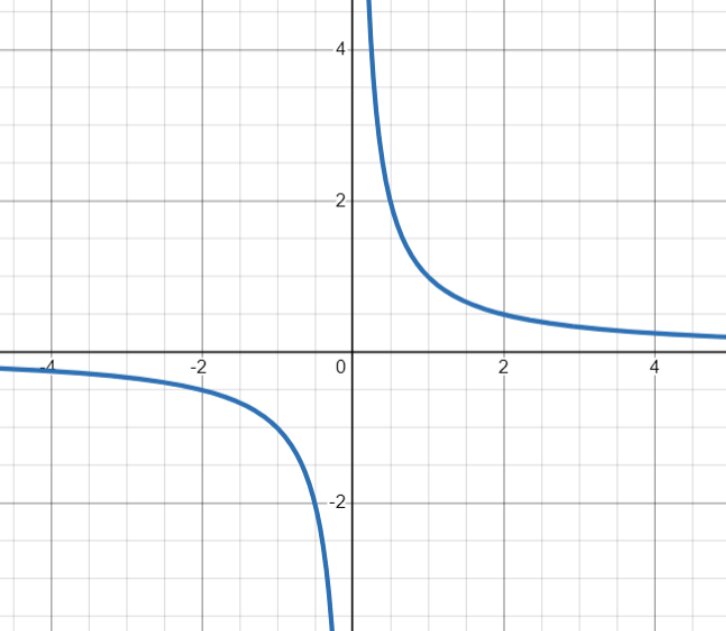
Answer: here, f(x) = 1 / x, and we know 1/ x is an infinitely differentiable function except x = 0 and the graph of f(x) = 1/x looks like: 

Now, differentiating f(x), we get

f(x) = 1/x => f(1) = 1/1

f’(x) = -1/x^2 => f’(1) = -1/1=-1

f’’(x) = 2/x^3 => f’’(1) = 2/1^3=2

f’’’(x) = -6/x^4 => f’’’(1) = -6/1^4=-6

Now, substituting the above values in the Taylor series formula, we get:

Programming Online Courses and Certification	Python Online Courses and Certifications
Data Science Online Courses and Certifications	Machine Learning Online Courses and Certifications

Now, we will discuss some commonly use Taylor Series Expansions:

Commonly used Taylor Series Expansion

Exponential Function

Logarithmic Function

Trigonometric Function

sin(x)

cos(x)

tan (x)

Conclusion

In this article, we have briefly discussed Taylor series approximation, the steps to find the approximation of a function and the application of how the Taylor series can be used in machine learning and deep learning.

Hope you will like the article.

Top Trending Article

Top Online Python Compiler | How to Check if a Python String is Palindrome | Feature Selection Technique | Conditional Statement in Python | How to Find Armstrong Number in Python | Data Types in Python | How to Find Second Occurrence of Sub-String in Python String | For Loop in Python |Prime Number | Inheritance in Python | Validating Password using Python Regex | Python List |Market Basket Analysis in Python | Python Dictionary | Python While Loop | Python Split Function | Rock Paper Scissor Game in Python | Python String | How to Generate Random Number in Python | Python Program to Check Leap Year | Slicing in Python

Interview Questions

Data Science Interview Questions | Machine Learning Interview Questions | Statistics Interview Question | Coding Interview Questions | SQL Interview Questions | SQL Query Interview Questions | Data Engineering Interview Questions | Data Structure Interview Questions | Database Interview Questions | Data Modeling Interview Questions | Deep Learning Interview Questions |