Tree Data Structure: Types, Properties, and Applications

Have you ever wondered how computers organize complex data efficiently? One answer lies in the tree data structure, a hierarchical model that resembles a tree in nature, with a single root leading to various branches and leaves, enabling quick data retrieval and manipulation. Let's understand more!

A data structure is a way of organizing, storing, and managing data to be used efficiently. Data structures are an important part of several computer algorithms and programs. They help programmers in designing efficient software. Data structures are used in all computer science domains, such as Artificial Intelligence and Operating systems. In this article, you will learn about one of the most popular non-linear data structures – Trees. This post will explore the different types of tree data structures, their properties, and the application of trees in the data structure.

Table of Content

• What is Tree in Data Structure?
• Tree Data Structure Terminologies
• Types of Trees
• Binary Trees
• Binary Search Trees
• AVL Trees
• B-Tree

Explore popular Data Structures and Algorithms Courses

Before I dive deep into the technicality of the topic, observe the below two diagrams representing members of the family and answer the question as follows: 

In the relation mentioned above if ‘A’ is the grandfather of ‘F’, and ‘C’ is the uncle of ‘D’. Which of the above diagrams would you choose to answer,

• Who is the father of ‘E’?
• What is the relation between D and E? 

From the second diagram, looking at the hierarchy, you can easily say that ‘B’ is the father of ‘E’, and D is E’s sibling.  

It was difficult to guess with the first representation of data. Well, the same is the case with computers. When the data is stored in a hierarchical form, it’s quicker for the computer to traverse it and find the results. 

Explore: What is Queue in Data Structure?

What is a Tree in Data Structure?

A tree data structure is a collection of nodes connected by edges. Each node contains a value or data which may or may not have a child node. The first node of the tree is called the root. If this root node is connected with another node, then this root is called the parent node, and the node connected to it is the child node.

When operations are performed in a linear data structure, the complexity rises as the data size increases. On the other hand, the tree data structure provides much quicker access to the data, which is non-linear. Let’s understand some of the terminologies associated with it.

Tree Data Structure Terminologies

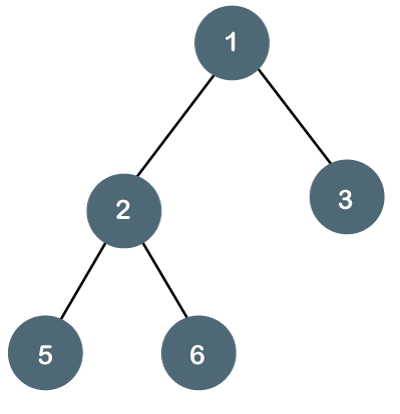
Terminology	Description	Example from Diagram
Node	Each vertex of a tree is a node.	‘1’, ‘2’, ‘3’ are the node in the tree.
Root	Topmost node of a tree.	Node ‘1’ is the topmost root node.
Parent Node	The node has an edge-sharing to a child node.	Node ‘2’ is the parent of ‘5’ and ‘6’, and Node ‘3’ is the parent of ‘7’.
Child Node	The sub-node of a parent node is the child node.	‘5’ and ‘6’ is the children of ‘2’.
Leaf	The last node which have any subnode is the leaf node.	‘5’, ‘6’, ‘9’ and ‘8’ are leaf nodes.
Edge	Connecting link between two nodes.	The link between ‘1’ and ‘2’, ‘2’ and ‘5’, ‘2’ and ‘6’ are edges
Siblings	Nodes with the same parent are siblings.	‘5’ and ‘6’ are siblings with ‘2’ as their parent.
Height	The height of a tree is the length of the longest path from the root to a leaf node. It is calculated with the total number of edges.	The height of ‘1’ is 3. (longest path is 1-3-7-9)
Depth	The number of edges from the root node to that node is called the Depth of that node. Depth of a tree = Height of tree – 1	The depth of root node ‘1’ is the height of ‘1’ – 1 = 2
Level	Each step from top to bottom is called a Level. If the root node is at level 0, its next child node is at level 1, its grandchild is at level 2, and so on.	‘1’ or root node is at level 0, ‘2’, ‘3’, and ‘4’ is at level 1, and so on.
Sub-Tree	Descendants of a node represent a subtree.	Nodes ‘2’, ‘5’, and ‘6’ represent a sub-tree.
Degree of Node	The degree of a node represents the total number of children in it.	The degree of ‘2’ is 2 (‘5’ and ‘6’). The degree of ‘4’ is 1.

Explore popular courses on Shiksha Online

Popular Programming Courses	Popular Big Data Courses
Best Cloud Technologies Courses	Best Databases Courses

Application of Tree Data Structure

File system: 

The files and folders in your Windows Explorer are stored in the tree format. In the below image, you can say that ‘My Computer’ is the root; Local Disk (C), Local Disk (D), and Local Disk (E) are basically the parent nodes and the files inside them are leaf nodes. This allows faster traversal of the nodes while jumping from one node to another.

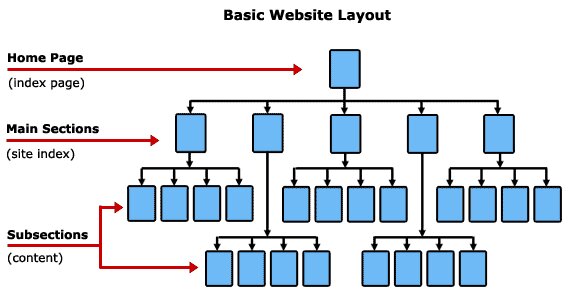
Webpage Layout

The layout of a webpage is designed in the tree structure. In the below diagram, the homepage or index page is our root node, main sections/ site index are their child nodes, which again are parents to multiple other child nodes (subsections).

Types of Tree Data Structure

The following are the different types of tree data structures:

• Binary Tree
• Binary Search Tree (BST)
• AVL Tree
• B-Tree

Binary Tree

A binary tree is a tree data structure in which each node can have 0, 1, or 2 children – left and right child.

Properties of a Binary tree

• The maximum number of nodes at any level ‘L’ in a binary tree is 2
• The minimum number of nodes in a binary tree of height H is H + 1
• The maximum number of nodes in a binary tree of height H is 2^H+1 – 1
• Total Number of leaf nodes in a Binary Tree = Total Number of nodes with two children + 1
• The maximum number of nodes at each level of i is 2ⁱ.
• Searching operation takes O(log2N)

Binary trees can be divided into the following types:

• Perfect binary tree: Every internal node has two child nodes. All the leaf nodes are at the same level.
• Full binary tree: Every parent node or an internal node has either exactly two children or no child nodes.
• Complete binary tree: All levels except the last one are full of nodes.
• Degenerate binary tree: All the internal nodes have only one child.
• Balanced binary tree: The left and right trees differ by either 0 or 1.

To learn more about binary trees, read our blog – Types of Binary Tree in Data Structure

Applications of Binary trees

• Decision Tree – Machine learning Algorithm

A supervised learning algorithm is used both in the case of a classification or regression-based problem. It starts with a root node and ends with a decision or prediction made by leaves. All the nodes in the tree represent a condition based on which the split occurs.

• Working with Morse Code

The organization of Morse code is done in the form of a binary tree

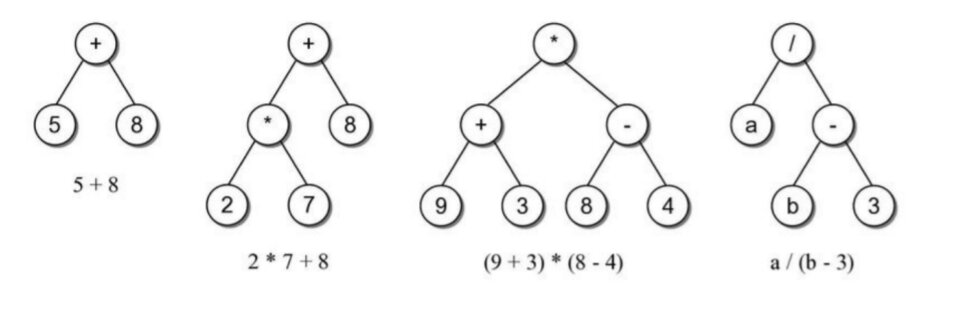
• Binary Expression Trees

A binary tree is used to evaluate an expression. The operators are stored at the interior node and the operands are stored at the leaf node.

Also Read: Top Universities Offering Free Online Programming Courses

Binary Search Tree (BST)

A binary search tree (BST) is also called an ordered or sorted binary tree in which the value at the left sub-tree is lesser than that of the root and the right subtree has a value greater than that of the root.

Every binary search tree is a binary tree. However, not every binary tree is a binary search tree. What’s the difference between a binary tree and a binary search tree? The most important difference between the two is that in a BST, the left child node’s value must be less than the parent’s, while the right child node’s value must be higher.

Properties of a Binary Search tree

• Each node has a maximum of up to two children.
• The value of all the nodes in the left sub-tree is less than the value of the root.
• The value of all the nodes in the right subtree is greater than or equal to the value of the root.
• This rule is recursively valid for all the left and right subtrees of the root.

Applications of a Binary Search Tree

• Used to efficiently store data in the sorted form to quickly access and search stored elements.
• Given ‘A’ a sorted array, determine how many times x occurs in ‘A’.
• Player ‘A’ chooses a secret number ‘n’. Player ‘B’ can guess a number x and A replies how x
• compares to n (equal, larger, smaller). What’s an efficient strategy for B to guess ‘n’?

Check out the Top Online Courses for IT Professionals

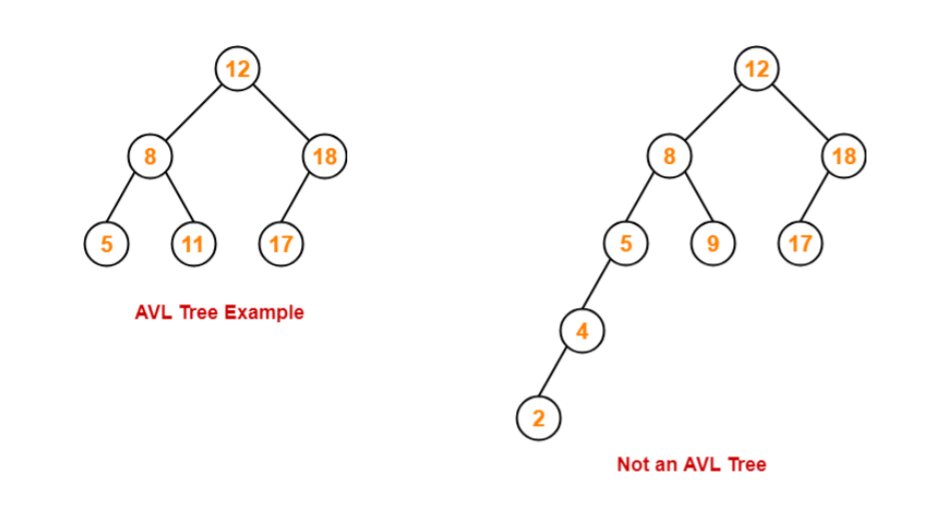
AVL Tree

AVL trees are a special kind of self-balancing binary search tree where the height of every node’s left and right subtree differs by at most one.

Properties of an AVL tree

• The heights of the two child subtrees of any node differ by at most one.
• Balance Factor = (Height of Left Subtree – Height of Right Subtree).
• -1 Balance factor represents that the right subtree is one level higher than the left.
• 0 Balance factor represents that the height of the left subtree is equal to that of the right subtree.
• 1 Balance factor means that the left subtree is one level higher than the right subtree.

• The maximum possible number of nodes in the AVL tree of height H is 2H+1 – 1
• The minimum number of nodes in the AVL Tree of height H is given by a recursive relation: N(H) = N(H-1) + N(H-2) + 1
• Minimum possible height of AVL Tree using N nodes = ⌊log2N⌋ i.e floor value of log 2N
• The maximum height of the AVL Tree using N nodes is calculated using recursive relation: N(H) = N(H-1) + N(H-2) + 1

Applications of AVL trees

• In-memory sorts of sets and dictionaries
• Database applications that require frequent lookups for data

Also Read: Top Online Courses to Learn Data Structures and Algorithms

B-Tree

B tree is a self-balancing search tree wherein each node can contain more than one key and more than two children. It is a special type of m-way tree and a generalized binary search tree. B-tree can store many keys in a single node and can have multiple child nodes. This reduces the height and enables faster disk access.

Properties of a B-Tree

• Every node contains at most m children.
• Every node contains at least m/2 children (except the root node and the leaf node).
• The root nodes should have a minimum of 2 nodes.
• All leaf nodes should be at the same level.

Application of B-trees

• Databases and file systems
• Multilevel indexing
• For quick access to the actual data stored on the disks
• To store blocks of data

Also Read: Top Data Structure Interview Questions [DS and Algorthims]

Conclusion

Data structures are the building block of programming languages. They are used in many areas of Computer Science for simple and complex computations. Good knowledge of Tree data structures is the foundation of writing good codes. It can help you to grow to new heights in your career and secure high-paying jobs in the programming world.

Read: 8 Most Important Data Structures Every Programmer Must Know