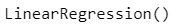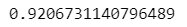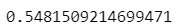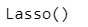Understanding Lasso Regression Using Python
Lasso is a regularization technique that reduces the model complexity by adding a penalty. The penalty minimizes the coefficient sizes and allows some of penalties to shrink to zero. This article briefly discussed how what is Lasso Regression and how to implement in python.
LASSO is a regularization technique used in Linear regression models for shrinkage and variable selection. Lasso imposes constraints on the parameters that cause the regression coefficient for some variables to shrink toward zero. The variables whose regression coefficient becomes zero are excluded from the model. The main goal of using lasso regression is to find the subset of predictors that minimizes the prediction error in the linear regression models.
Before discussing lasso regression, let’s discuss an important topic: “What is Regularization?”
Regularization is used in machine learning models to prevent the model from overfitting by adding penalties.
- In regularization, we reduce the magnitude of the coefficients
There are two types of regularization techniques that are used to reduce the regression coefficient or magnitude of the coefficient:
- Lasso Regression (also referred to as L1 regularization)
- Ridge Regression (also referred to as L2 regularization)
This article will briefly discuss how to use lasso regression in a linear regression model.
So, without further delay, let’s dive deep to learn more about lasso regression.
Table of Content
Best-suited Machine Learning courses for you
Learn Machine Learning with these high-rated online courses
What is Lasso Regression?
LASSO stands for Least Absolute Shrinkage and Selection Operator.
Lasso regression is a regularization technique that reduces the model complexity by adding a penalty.
- Lasso penalizes the model based on the sum of the Absolute Coefficient Values, also referred to as the L1 penalty.
- L1 penalty minimizes the coefficients’ size and allows some penalties to shrink to zero.
- The variables whose regression coefficient becomes zero are excluded from the model.
- In lasso, the data values are shrunk towards a central point such as the mean value.
- It is mainly used if the dataset has high dimensionality and high correlation.
Note: A hyperparameter lambda is used (multiplied) with the L1 penalty to control the weight of the penalty.
Mathematical Formula of Lasso Regression
The mathematical equation for the lasso regression will be:
Residual Sum of Square + lambda * (sum of the absolute value of the magnitude of the coefficient)
i.e.,
| Programming Online Courses and Certification | Python Online Courses and Certifications |
| Data Science Online Courses and Certifications | Machine Learning Online Courses and Certifications |
Implementation of Lasso Regression in Python
About Dataset
The data was extracted from the 1974 Motor Trend US magazine and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models). The data set is used to implement Lasso Regression to improve the r2 score of the model.
A data frame with 32 observations on 11 (numeric) variables and 1 categorical variable.
mpg: Miles/(US) gallon
cyl: Number of cylinders
disp: Displacement (cu.in.)
hp: Gross horsepower
drat: Rear axle ratio
wt: Weight (1000 lbs)
qsec: 1/4 mile time
vs: Engine (0 = V-shaped, 1 = straight)
am: Transmission (0 = automatic, 1 = manual)
gear: Number of forward gears
Step – 1: Import Dataset
#import Libraries
import pandas as pdimport numpy as np
#import the dataset
mt =pd.read_csv('mtcars.csv')
#check the first five rows of the data
mt.head()
Step – 2: Check for Null Values
#check for null values
mt.info()
In the above dataset, no feature contains the NULL values.
Step-3: Drop the Categorical Variable
#drop the categorical variable: model from the dataset
mt.drop(['model'], axis = 1, inplace = True)mt
Step -4: Create Feature and Target Variable
#create feature and Target Variable
x = mt.drop(columns = 'hp', axis = 1)y = mt['hp']
Step- 5: Train- Test Split
#splitting the data into train and test set
from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 4)
Step – 6: Fitting into the model
#fitting data into the model
from sklearn.linear_model import LinearRegression
lr = LinearRegression()lr.fit(x_train, y_train)
Step – 7: Checking r-squared value
#import r2_score
from sklearn.metrics import r2_score
#r2-score for train data
x_pred_tarin = lr.predict(x_train)r2_score(y_train, x_pred_train)
#r2-score for test data
x_pred_test = lr.predict(x_test)r2_score(y_test, x_pred_test)
Step – 8: Building LASSO Model
from sklearn.linear_model import Lasso
lasso = Lasso()lasso.fit(x_train, y_train)
x_pred_lasso_test = lasso.predict(x_test)r2_score(y_test, x_pred_lasso_test)
From above, we get the r2_score increases after implementing lasso changes from 0.54 to 0.78.
Conclusion
Lasso is a regularization technique that reduces the model complexity by adding a penalty. The penalty minimizes the coefficient sizes and allows some of penalties to shrink to zero. This article briefly discussed how what is Lasso Regression and how to implement in python.
Hope this will help you to learn all about LASSO and clears all your doubts.
Top Trending Article
Top Online Python Compiler | How to Check if a Python String is Palindrome | Feature Selection Technique | Conditional Statement in Python | How to Find Armstrong Number in Python | Data Types in Python | How to Find Second Occurrence of Sub-String in Python String | For Loop in Python |Prime Number | Inheritance in Python | Validating Password using Python Regex | Python List |Market Basket Analysis in Python | Python Dictionary | Python While Loop | Python Split Function | Rock Paper Scissor Game in Python | Python String | How to Generate Random Number in Python | Python Program to Check Leap Year | Slicing in Python
Interview Questions
Data Science Interview Questions | Machine Learning Interview Questions | Statistics Interview Question | Coding Interview Questions | SQL Interview Questions | SQL Query Interview Questions | Data Engineering Interview Questions | Data Structure Interview Questions | Database Interview Questions | Data Modeling Interview Questions | Deep Learning Interview Questions |
Vikram has a Postgraduate degree in Applied Mathematics, with a keen interest in Data Science and Machine Learning. He has experience of 2+ years in content creation in Mathematics, Statistics, Data Science, and Mac... Read Full Bio
Top Picks & New Arrivals
