What to keep in mind for CAT Quantitative Aptitude preparation?

CAT Quantitative Aptitude has the potential of 100 percentile if you prepare well. The Quantitative Aptitude topics of CAT are advance level Mathematic topics from Class 9 and 10. So, for any candidate, the foundation is already there, they only need to work on it further. The important topics of CAT Quantitative Aptitude include Geometry, Ratios and Proportion, Inequalities, Trigonometry, In-equations, Quadratic and Linear Equations, Work and Time, Algebra, Surds and Indices, Percentages, Mensuration, Time-Speed-Distance, Logarithms, Partnership (Accounts), Number System, Square Root and Cube Root, Profit & Loss, Geometric Progression, Probability, Mean-Mode-Median, Binomial theorem, Simple interest and compound interest. Maximum questions are asked from Arithmetic and Geometry so keep the main focus on these two topic. Understand and memorise the formulas and theorems well, and practice enough questions to be thorough with their application.

How to prepare for AFCAT Quantitative Aptitude section?

Practice and revise topics such as Time & Work, SI, Profit & Loss, Percentages, Series Completion, DI, etc. Learn the logic behind the formulas and shortcut tricks of solving questions. Candidates need to clear the concepts of every topic so that they can solve the questions easily. The tips and tricks to crack AFCAT Numerical Ability section are given below: Candidates must write down all the formulae in one place so that they easy access to them during revision Candidates must work on the topics that have more weightage in the exam first Candidates must solve Numerical Ability questions daily to get the concepts clear Candidates must refer to the good books for Numerical Ability section

How many questions are there in the Quantitative Aptitude section of the XAT exam?

The number of questions in the Quantitative Aptitude (QA) section of the XAT exam can vary from year to year, but typically there are around 25-27 questions in this section. The QA section is designed to test a candidate's mathematical and analytical skills, and it covers topics such as arithmetic, Algebra geometry, Trigonometry Probability and Statistics. The questions in the QA section are of varying difficulty levels, and the section is generally considered to be one of the more challenging sections of the XAT exam. To score well in this section, it is important to have a strong foundation in mathematics, as well as the ability to solve problems quickly and accurately under time pressure. It is recommended that candidates practice a wide variety of QA questions and take regular mock tests to improve their speed and accuracy. Additionally, candidates should also focus on developing their time management skills and prioritizing questions based on their level of difficulty to maximize their overall score in the QA section. Please upvote if it was helpful.

What is the difficulty level of the Quantitative Aptitude questions in XAT?

The difficulty level of the Quantitative Aptitude (QA) section in XAT varies from year to year, but generally, the QA section is considered to be moderately difficult to difficult. The questions in this section are designed to test a candidate's mathematical and analytical skills, and they cover a wide range of topics, including arithmetic, Algebra geometry, Trigonometry Probability and Statistics. The QA section of XAT often includes questions that are complex and require a high level of mathematical proficiency. The questions may be in the form of data interpretation or require candidates to use logical reasoning and critical thinking skills to arrive at the correct answer. To score well in the QA section of XAT it is important to have a strong foundation in mathematics and practice a wide variety of questions from different sources. Candidates should focus on developing their problem-solving and time management skills and work on improving their speed and accuracy in solving QA questions. Overall, the QA section of XAT can be challenging, but with proper preparation and practice, candidates can improve their performance and score well in this section. Please upvote if it was helpful.

What makes CAT tougher than other MBA entrance exams?

CAT exam is a national level MBA entrance exam conducted by the IIM. Every year, over 2.3 Lacs candidates apply for it. The CAT score is accepted by the Iims and all top MBA colleges in India. To select the best candidates from over 2.3 Lacs test takers there is a need for tough criteria. That's why, the CAT exam is tougher than other MBA entrance exams. Even though the syllabus of CAT is same as that of other MBA entrance exams, the question paper set by the IIM faculty always has tough questions. Moreover, CAT has sectional time limit for each section which is not there in any other exam expect XAT. Having a time limit for each section adds pressure on candidates to complete solving adequate number of questions in a section within the time limit. If a student is weak in a particular subject, they can't use the time as per their need. CAT's Reading Comprehension passages are long and dense unlike other MBA exams. This is one more reason why most candidates feel CAT is tougher than any other MBA entrance exam.

How many CAT mock tests to practice to score 99 percentile?

Experts recommend that aspirants must practice at least 40 CAT mock tests to score above 99 percentile well in the exam. Most of the CAT test takers take up to 50 mock tests of various types and difficulty level. CAT toppers in previous years have practiced even up to 80 mock tests during their preparation. However, candidates must decide the number of CAT mock tests depending on their control and confidence on topics as the exam day comes closer. Mock tests are the best way to judge your performance viz. The important topics of CAT. The more one practices CAT mock tests, the more accurate they get in solving questions from all subjects. It is very important to know which formula to apply to which type question to solve the problem accurately. Mock tests help candidates in this aspect which is why practicing mock tests is most important in CAT preparation.

When should I start practicing XAT mock tests?

Aspirants should start practicing XAT mock tests after completing the syllabus. The ideal time duration to solve XAT mock tests is October to December. Avoid practicing mock tests before completing the syllabus. The official mock test is released a week before the exam, so candidates must attempt it at least once before the exam. The official and unofficial mock tests are same as the actual XAT exam so that the candidates can get familiar with the exam pattern, test structure of the question paper and get used to handling the exam pressure. It is important to practice XAT mock tests so that you have prior experience of XAT exam. Both official and unofficial XAT mock tests helps in improving accuracy of solving questions because in an exam like XAT all that matters is speed with accuracy.

What is the latest CMAT exam pattern?

The latest CMAT exam pattern as prescribed by the National Testing Agency NTA is as follows: The question paper carries 100 question. The format of questions is multiple choice type where for each question, four options are given to choose the correct answer from. The 100 questions are divided equally between five sections, Quantitative Techniques and Data Interpretation, Language Comprehension, Logical Reasoning, General Awareness and Innovation and Entrepreneurship. Each of the five sections carry 20 questions. Earlier, there were only four sections in CMAT and each section has 25 questions. In 2021, Innovation and Entrepreneurship was added as the fifth section. The time limit for CMAT is 180 minutes without sectional time limit or break. As per the latest marking scheme, for every correct option 4 marks are awarded and for every incorrect option, one mark is deducted. There is no negative marking for unanswered questions.

If I am preparing for CAT, do I need to prepare separately for CMAT?

If you are preparing for CAT your work is almost over for CMAT. I was also a student who prepared for CAT immediately after my graduation. The important things which you should look into while preparing for this exam are as follows: 1. Select one of the best coaching centers which offer quality education- TIME is one of the famous coaching centers for CAT. 2. Dedication- Be focused on the aim which you need to achieve. 3. Try to read Hindu newspaper editorial. Most of the passages which appear in CAT are from Hindu editorial. 4. Try to maximum number of online mock test. You will definitely clear CAT by doing the above. 5. Try to read as much as you can and make note of points. 6. Revision of each week topics is very important. 7. Mathematical ability questions will be little twisted try to do as faster as you can.

How can I improve my score in Quantitative Aptitude section of CAT?

The key to improving score in Quantitative Aptitude section of CAT is practice, practice and more practice. Listed below are some tips you can apply while preparing for CAT. Practice Mental Maths to be less dependent on calculators Make short notes of formulae and sample questions to revise them on the go Develop the ability to choose which questions to answer in the exam Avoid negative marking. Don’t attempt questions you are not sure of Practice Quants questions in a time bound manner to be able to utilize maximum time in the main exam Solving a sample question is not enough. Practice the same set of questions multiple time

What is the weightage of Quantitative Aptitude in MBA exams?

The Quantitative Aptitude section is one of the main sections of any MBA exam. It usually has one 1/3 rd (exams having three sections in total) or 1/4 th (exams having four sections in total) weightage in the question paper. Check below the weightage of Quantitative Aptitude in top MBA entrance exams. CAT Quantitative Aptitude questions: 22 XAT Quantitative Aptitude questions: 27 CMAT Quantitative Aptitude questions: 25 SNAP Quantitative Aptitude questions: 20 IIFT Quantitative Aptitude questions: 25 MAT Quantitative Aptitude questions: 40 ATMA Quantitative Aptitude questions: 60 MAH CET Quantitative Aptitude questions: 50

What should be my approach towards Quantitative Aptitude on CAT exam day?

Quantitative Aptitude is the last section of CAT. By the time you reach this section, it is natural for fatigue to set it. Don’t get bogged down by fatigue. Stay energized and alert as this section requires Mathematical calculations. Read the questions calmly and then choose the ones you can solve with maximum accuracy. The CAT Quantitative Aptitude section is dominated by Mensuration and Arithmetic, so have a good control on those topics. Do not spend too much time on any question that is posing a challenge to you. Do not get greedy and fall in the trap of negative marking.

Is XAT tough for candidates from non-Engineering background?

Yes, XAT is slightly tougher for candidates with non-Engineering background as the Quantitative Aptitude section is of higher difficulty level. However, they can crack it if they work on the fundamentals of Math and practice questions of all difficulty levels. It will take time but they will be able to crack XAT's quant section if they dedicate extra hours to it. Aspirants can find XAT study material online in various online study groups. Students’ groups on Facebook, WhatsApp, Telegram, etc. share study material with each other. One can also download MBA exam preparation apps to get relevant and useful study material. The good part about XAT is that, it has different cut offs for candidates belonging to different academic backgrounds. As part of its commitment to academic diversity, the institute has lower cut offs for candidates from non-engineering background than candidates from engineering background.

Are six months enough to prepare for CAT?

Usually, it is recommended to start CAT preparation about a year or nine months in advance. However, one can prepare for this exam even in six months if they put 8-10 hours daily into it. Candidates who have attempted the CAT before may not face a lot of hurdles in six-month preparation as they have a foundation in CAT preparation from previous year, but candidates who are appearing in the exam for the first time may face obstacles, mostly related to accuracy. The syllabus of CAT is vast and includes a lot of reading. One also has to spend a lot of time in practice sessions and mock tests to be able to master all types of CAT questions - easy, moderate and tough. If you are a student of engineering/technical or commerce background you will need to pay extra attention on VARC . However, you'll be able to manage the syllabus of DILR and Quantitative Aptitude with adequate practice of topics. But if you are a student from Arts background, it is advised to start CAT preparation much earlier because you will have to brush up a lot of Mathematics. Reading Comprehension is one subject that cannot be mastered by student belonging to any academic stream, if their English comprehension is not strong. To develop reading habit all CAT aspirants will have to start much earlier.

What is the difficulty level of MAH MBA CET?

MAH MBA CET is a moderately difficult exam. It’s difficulty level is lower than CAT but higher than MAT or ATMA. A major factor that makes MAH CET a difficult test to crack is that the questions are presented in random order and sectional weightage vary in every slot. So, candidates cannot anticipate or plan how many and which type of questions to get to their target score. Also, the MAH MBA CET is dominated by Logical Reasoning questions and there are comparatively less Quantitative Aptitude questions. Since, there is no set pattern, candidates cannot pre-plan. They need to make a strategy and implement it as soon as they see the question paper. So, those who can think on their feet and can crack the exam better than others.

How to start preparing for quant from basics?

In Simple words to become good in Quant you need practice on daily basis, it is the only way to score good in quantitative aptitude Quantitative is most scoring part and merit deciding part of any competition job Tips to prepare for bank exams and crack the Quantitative Aptitude section with ease 1. Basic Concepts: 2. Basic formulas and identities: 3. Make your own shortcuts and tricks: 4. Practice as this is the only key to success: 5. Time management: I will strongly recommend you these books for basics Quantitative aptitude by. DR. R. S. AGGARWAL

Which are the most important Quantitative Aptitude topics?

Some of the most important topics of Quantitative Aptitude are Line, Angles, Triangles, Quadrilaterals, Polygon, Circles, Ares, Volume, Height and Distance, Co-ordinate Geometry, Basic Trigonometry, Numbers, Percentage, Profit & Loss, Simple and Compound Interest, Ratio, Proportionality, Time-Distance, Time-Work, Mixtures, Averages, Partnership, Permutation and Combinations, Probability, Set Theory, Progression and Series, etc. In all MBA entrance exams and most of the competitive exams, the questions of Quantitative Aptitude are asked from these topics. In CAT/XAT/NMAT/SNAP/CMAT and other exams, Mensuration, Arithmetic and Geometry topics dominate the test. If you are preparing for MBA entrance exams, then your main focus should be on these topics.

Can I score well in Quantitative Aptitude just by practicing sample questions?

To score well in Quantitative Aptitude one needs to first master all the concepts and theorems. If you are good at Mathematics or studied it in Graduation, you can score well by just practicing a variety of sample questions for over a period of two to three months. Practice Mental Maths for quick calculation and memorise a minimum of Tables till 20, Squares up to 100, Square roots from 1 to 25, Cubes up to 30. These will help you immensely in cracking Quantitative Aptitude section as well as the Data Interpretation section. Infact, in some exams Quantitative Aptitude and Data Interpretation are clubbed together as both have Mathematic based questions and require calculation to arrive at the answer. It is because similarity of the nature of the subjects, they are clubbed together in some MBA entrance exams.

Is it easier to crack Quantitative Aptitude than Verbal Ability and Reading Comprehension?

One can say it is easier to crack Quantitative Aptitude as it all about concepts, theories and practice. If you have practiced enough, you’ll know the types of questions that will be asked in the exam. However, Verbal Ability & Reading Comprehension, there is no guarantee that you would be familiar with the RC passage in the exam. In CAT, RC passages are inference based, in XAT some RC passages are in the form of poem and in SNAP/IIFT, the passages are facts based. The Quantitative Aptitude section of all the exams are of same type with only different difficulty levels. Thus, you need to put in extra effort in VARC.

Can I prepare for XAT with CAT preparation material?

Yes, you can definitely use CAT (Common Admission Test) preparation material to prepare for XAT (Xavier Aptitude Test), as there is a significant overlap in the syllabus and level of difficulty between the two exams. Both CAT and XAT have sections on Quantitative Ability, Data Interpretation, Verbal Ability, and Logical Reasoning, which are common to both exams. However, XAT also has a separate section on Decision Making, and a section on General Knowledge, which is not present in CAT. So, while the preparation material for CAT can provide a good foundation for the common sections of XAT candidates should also practice specifically for Decision Making and General Knowledge sections, using appropriate study material and resources. In addition to CAT preparation material, candidates can also refer to XAT-specific preparation books and study material to get a better understanding of the exam pattern and type of questions asked in XAT. It's important to note that while the preparation material is important, the key to success in XAT is consistent practice and thorough understanding of concepts. So, candidates should focus on building their conceptual clarity, practicing regularly, and analyzing their performance to identify areas of improvement.

How can I master Logical Reasoning and Data Interpretation topics of CMAT?

Cracking Logical Reasoning section of CMAT is all about how well and how quickly you understand the puzzles and patterns. To master this section of CMAT exam, sample questions for practice and sectional mock tests for CMAT are the best resource. You should start practicing Logical Reasoning questions early on in the preparation cycle. Pay attention to the topics from which Logical Reasoning questions are asked in CMAT. Prepare for those type of questions only. For Data Interpretation section of CMAT. You should be well versed with reading tables, graphs and charts correctly. For quick calculation, you should strengthen basic mathematical calculations like multiplication, division, square, square roots, cube, cube roots, etc. This section is all about observation and ability to break down information into pieces, so you need to practice a wide range of data interpretation questions.

What are the important topics of IIFT Quantitative Aptitude syllabus?

Quantitative Aptitude section of IIFT entrance exam comprises all the topics of Geometry, Algebra, Number System, Arithmetic, Mensuration, Trigonometry and Modern Math, etc. that include Percentages, Number System, Binomial Expansion, Arithmetic Progression, Simple Interest, Ratios, HCF & LCM, BODMAS, Median, Compound interest, Arithmetic Mean, Co-ordinate geometry, Standard Deviation, Vectors, Set Theory, Instalments/ payments, Permutation & Combination, Mode, Trigonometry, Mensuration, Probability, Clocks & Calendar, Time, Speed, Distance, Logarithm, Geometric Progression, Averages, In- equations Quadratic, Profit & Loss, Venn Diagram, Geometric Mean, Ratios & Proportions, Linear Equations, Algebra, Geometry, Work & Time, Harmonic Mean. Candidates must start preparation of IIFT Quantitative Aptitude section about 6-8 months in advance so as to be able to have enough time to complete the syllabus and practice sample questions. This section also requires practice of sample questions as mere theoretical understanding is not enough. The need for speed and accuracy is critical for IIFT exam so candidates must focus on gaining conceptual clarity of every topic and correct application for the theorems and formulae. Having a mentor or guide will be helpful so join a coaching institute or online study groups.

Should I take coaching for SNAP preparation?

Yes, coaching is recommended for preparation for any competitive exam as the candidate gets best of aid such as books, study material and mentors. However, the candidates must join coaching if only they can follow the rigorous time-table and daily classes. About six to eight hours daily is considered good enough duration for SNAP preparation. However, if you start exam preparation late (by October) then you need to devote 10-12 hours daily. SNAP is easy and if you are preparing for other MBA entrance exams, you may not need to work too hard on it. A good number of sample papers and mock tests will be good enough. Some of the most recommended books include: How to Prepare for Data Interpretation for CAT How to Prepare for Logical Reasoning for the CAT by Arun Sharma High School English Grammar & Composition by Wren & Martin

Which are the best books for CMAT Quantitative Aptitude preparation?

The Quantitative Aptitude section of CMAT has questions from Arithmetic, Geometry, Modern Math, Numbers, Algebra and Data Interpretation. The questions are of moderate difficulty level and one can prepare for it with the help of best books for CMAT recommended by experts and toppers. We have listed down some of the popular CMAT books that candidates usually refer: 1. NCERT Mathematics Books for Class 8, 9 and 10 2. The Pearson Guide to Quantitative Aptitude for Competitive Exams 3. How to Prepare for Quantitative Aptitude for CAT Arun Sharma (Mc Graw Hill Education) 4. Quantitative Aptitude Quantum CAT Common Admission Tests for Admission into Iims by Sarvesh K Verma (Arihant) 5. Quantitative Aptitude for Competitive Examinations by Abhijit Guha (Mc Graw Hill Education) 6. Quantitative Aptitude for Competitive Exams by RS Aggarwal.

Which is the best book for the Quantitative Aptitude section of XAT?

There are several good books available for the Quantitative Aptitude section of XAT (Xavier Aptitude Test). Here are some of the most popular and highly recommended ones: 1) Quantitative Aptitude for Competitive Examinations by R. S. Aggarwal: This is one of the most popular books for Quantitative Aptitude and is useful for XAT as well as other competitive exams. 2) How to Prepare for Quantitative Aptitude for CAT by Arun Sharma: This book is specifically designed for CAT but the concepts and practice questions are also useful for XAT preparation. 3) Quantitative Aptitude Quantum CAT Common Admission Tests For Admission into Iims by Sarvesh K. Verma: This book is focused on CAT but also covers the relevant concepts and practice questions for XAT. 4) Quantitative Aptitude for MBA Entrance Examinations by Abhijit Guha: This book is specifically designed for MBA entrance exams, including XAT. And covers all the relevant topics with detailed explanations and practice questions. 5) The Pearson Guide to Quantitative Aptitude for MBA Entrance Examinations by Dinesh Khattar: This book provides a comprehensive coverage of the Quantitative Aptitude section of MBA entrance exams and includes a large number of practice questions with detailed explanations. It's important to note that while the books mentioned above can be helpful, candidates should also practice solving previous years' XAT papers and attempt mock tests to get a better understanding of the exam pattern and the type of questions asked. Consistent practice and conceptual clarity are key to succeeding in the Quantitative Aptitude section of XAT.

Which are the best books for the Quantitative Aptitude section for ATMA exam?

The best books for Quantitative Aptitude preparation of ATMA exam are listed below. These are the recommended books by experts. 1. NCERT Mathematics books (Class 9-10) 2. Quantitative Aptitude for Competitive Examinations by Abhijit Guha 3. Quantitative Aptitude by RS Aggarwal The NCERT Mathematics book is recommended for ATMA preparation because it is the best source of building or revisiting the fundamentals of Algebra Geometry, Trigonometry Mensuration Number Systems and Arithmetic. The NCERT books are extremely helpful to students from non-Engineering background. Quantitative Aptitude books by Arun Sharma, Abhijit Guha, Nishit Sinha and RS Aggarwal are the main books for ATMA preparation as well as other MBA entrance exams such as CAT. These books cover all the topics at intermediate and advanced level. They also have many sample questions of easy, moderate and high difficulty levels for practice.

What is the sectional weightage of Quantitative Aptitude in CAT?

The Quantitative Aptitude section of CAT is the third and the last section of the question paper. It has 22 questions and the total marks is 66. This section of the CAT exam is usually dominated by Arithmetic and Algebra. Most of the questions out of 22 are asked from these two topics. In CAT 2022, there were about 7-9 Algebra questions and 7-9 Arithmetic questions (the exact number varied for all three slots). Apart from these two topics, there are questions from Mensuration Modern Math and Number System in the Quantitative Aptitude section CAT. Some of the important sub topics in this section include: Arithmetic topics: Ratio and Proportion, Simple and Compound Interest, Profit and Loss Mixtures and Allegations Averages, Percentages, Mean Median Mode, Time and Work, Time Speed and Distance Algebra topics: Basics Algebraic Formulae, Number of integer solutions, Quadratic Equations, Finding out roots, Maxima and Minimal, Higher Degree Equations, Linear Equations, Problems on ages, Descartes Rule of Signs, Inequalities, Logarithm, Functions, Modifications of Graphs, The smallest Value in a Maximum Function Number System topics: Finding Out Last Two Digits, Number of Trailing Zeroes, Finding out Remainders based on, Basic Divisibility Rules, Binomial Theorem, Simplifying the Dividend (Single and/or Multiple Divisors), Basics of Numbers, Properties of Numbers, Divisibility Rules, Divisibility and Factors, the highest Common Factor and the lowest Common Multiple, Finding Out the Last Digit, Fermat's Theorem, Euler's Theorem, Pattern Recognition and Cyclicity of Remainders, Wilson's Theorem, Base Systems, Conversion of Bases, Addition/Subtraction/ Multiplication in different bases Geometry Topics: Lines and Angles, Triangles Basic Concepts, Area, Angles, Similar Triangles Polygons, Circles, Solids / Mensuration 3D Geometry, Coordinate Geometry, Trigonometry Modern Math topics: Sequence and Series Binomial Theorem, Set Theory, Permutation and Combination, Probability.

What is the MAT syllabus for Mathematical Skills?

Some of the main topics included in the MAT syllabus for Mathematical Skills are LCM and HCF, Percentages, Commercial Maths Complex Numbers, Percentages, Profit and Loss, Permutation and Combinations, Binomial Theorem, Sequence and Series Surds and Indices, Interest (Simple and Compound), Heights and Distance, Inequalities, Speed, Time and Distance, Triangles Set Theory, Number System Circles, Mixtures and Alligations, Elementary Mathematics, Geometry, Venn Diagrams, Trigonometry Equations and Linear Programming. Candidates need to study all these topic thoroughly this section of MAT carries 40 questions and in every session there can be more questions from any topic. So, start preparing for Mathematical Skills section of the MAT exam at least six months before you intend to appear for it. To cover the entire syllabus of this section thoroughly, you will need at least six months.

What is the SNAP syllabus for Quantitative Aptitude?

SNAP syllabus for Quantitative Aptitude includes topics of Data Interpretation as well. Candidates have to study Algebra, Geometry, Trigonometry, Mensuration, Number System, Logarithm, Linear Equations & Quadratic Equations, Set Theory, Arithmetic, Progressions, Binomial Theorem, Surds and Indices, Inequalities, Permutation & Combination, Probability Functions, Mixtures & Alligations, Co-ordinate Geometry, Series, Graphs-Pie Chart, Bar Graphs and Tables as part of SNAP Quantitative Aptitude syllabus. The SNAP Quantitative Aptitude section includes Data Interpretation and Data Sufficiency. The total number of questions in this section is 20 and the section is dominated by Arithmetic. Since the past two years, no Data Sufficiency questions have been asked. So, candidates must focus more on Quantitative Aptitude while preparing for the SNAP exam. This section is all about accuracy so have complete clarity of concepts and theorems.

Mensuration Formula, Definition, Rules, Sample Questions, Tips and FAQs

15.1K Views

This chapter has multiple topics listed below:

Quantitative Aptitude Permutation and Combination Probability Interest and Simple Interest Fo...Square Root and Cube Root Mean Mode Median Mensuration Formula Binomial Theorem

Vipra ShrivastavaSenior Manager - Content

Updated on Nov 26, 2024 16:04 IST

Mensuration is a chapter in Mathematics that we all have studied in school. It forms an important section of test in various entrance exams for professional courses and competitve exams too. In MBA, Mensuration is an important chapter in Quantitative Aptitude section. It carries significant weightage in MBA entrance exams like CAT, XAT, CMAT, NMAT, SNAP, MAT, ATMA and others. Read here more about Mensuration.

Table of Contents

What is Mensuration?
Mensuration Formulas
Illustrated Examples of Mensuration Formulas
CAT Quantitative Aptitude Questions for Practice with Solutions
FAQs Related to Mensuration and Mensuration Formulas

What is Mensuration?

Mensuration can be defined as the measurement of geometric figures such as quadrilaterals, their areas, perimeter, surface areas, and volumes. It is a very important topic in CAT and other MBA entrance exams. Mensuration questions are also asked in other competitive exams, so if you are preparing for any entrance or competitve exam, then you must prepare Mensurarion thoroughly.

Mensuration Formulas

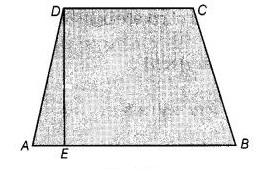
Trapezium:

A trapezium is outlined by a form that has 2 parallel sides and the other 2 are nonparallel. It has four sides and four vertices.

Shape	Area	Perimeter
1. Trapezium	Area= (1/2) H + (AB+CD)	P= sum of all the sides i.e. AB+BC+CD+AD
2. General quadrilateral	Area= Area of △ABC + Area of △ADC	The perimeter depends on the type of shape which is present
3. Special quadrilateral (rhombus)	½ × d₁ × d₂	P=4a

Where, H= height, W= breadth, a,b,c,d= sides, d= diagonals.

Surface area: It is the the total area of all the surfaces of any form.

Volume: the degree is outlined by the number any third-dimensional form takes.

Shape	Surface area	Volume
1. Cube	Area= 6a^2	V= a^3
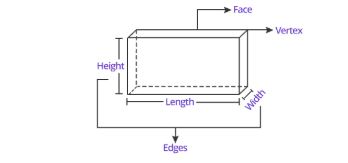
2. Cuboid	Area= 2 [(l × b) + (l× h) + (b× h)]	V= lwh
3. Cylinder	Ares= 2πr (r + h)	V= πr2 × h

Where, H= height, a= sides, r= radius, d= diameter, b= breadth, w= width

Also Read: MBA Preparation 2024: Tips to Prepare for MBA Entrance Exams

Illustrated Examples of Mensuration Formulas

Example 1: Calculate the area of a rhombus whose diagonals are 10 cm and 8.2 cm of length.

Ans: The formula for calculating area of a rhombus = ½ d1d2, (d1 and d2 are the lengths of the diagonal)

a= 2 × 10 × 8.2 cm2 = 41 cm2.

Example 2: A rhombus with an area of 240cm2 and whose one diagonal is of length 16 cm. Find the other diagonal.

Ans: We know d1 = 16 cm and let the other diagonal = d2

Thus the area of the rhombus = 2 d1 . d2 = 240

So, ½ 16 d2 = 240

Therefore, d2= 30cm

Diagonal 2 is 30 cm.

CAT Quantitative Aptitude Questions for Practice with Solutions

Get here sample questions and practice tests of how to prepare for Quantitative Aptitude for CAT pdf with solutions for practice.

CAT Quant_Easy-Test_1_Questions	CAT Quant_Easy Test 1_Solutions
CAT Quant_Medium_Test_1_Questions	CAT Quant_Medium_ Test 1_Solutions
CAT Quant_Difficult_Test_1_Questions	CAT Quant_Difficult_Test 1_Solutions

CAT Quant_Easy Test 2 Questions	CAT Quant_Easy Test 2 Solutions
CAT Quant_Medium Test 2 Questions	CAT Quant_Medium Test 2 Solutions
CAT Quant_Difficult Tes 2 Questions	CAT Quant_Difficult Test 2 Solutions

CAT_Quant_Easy_Test-_Set_3	CAT_Quant_Easy_Test_-_Set_3_Solutions
CAT_Quant_Medium_Test_-_Set_3	CAT_Quant_Medium__Test_Set_3_Solutions
CAT_Quant_Difficult_Test_-_Set_3	CAT_Quant_Difficult_Test_-_Set_3_Solutions

CAT_Quant_Easy_Test_Set_4	CAT_Quant_Easy_Test_Set_4_Solutions
CAT_Quant_Medium_Test_Set_4	CAT_Quant_Medium_Test_Set_4_Solutions
CAT_Quant_Difficult_Test_Set_4	CAT_Quant_Difficult_Test_Set_4_-Solutions

FAQs Related to Mensuration and Mensuration Formulas

Q: What is the formula of the area of a cube?

A: The Formula for area of sq. can be: Area=6a^2 Where a= sides of the cube

Q: What is the area of the quadrilateral?

A: The area of the quadrilateral depends on the form of that specific quadrilateral. Example: area of general quadrilateral = space of △ABC + Area of △ADC.

Q: What is the height of a cylindrical structure?

A: The height of a cylinder is calculated by multiplying the world of the cylinder’s base (the circle) with its height.

Q: How many edges and faces will a cuboid have?

A: A cuboid has 6 faces, 12 edges.

Q: What is the area of a cuboid?

A: Surface area= Area= two [(l × b) + (l× h) + (b× h)] Where, l= length, h=height, b= breadth

MBA exams you must check out

Exams for which registrations will start soon

Upcoming registrations

VEE

VEE 2025 Application Form

Jan '25 - Apr '25

View allMBA exams

News & Updates

Latest NewsPopular News

Download Important Dates for MBA/PGDM Exams

Quantitative Aptitude Prep Tips for MBA Exam

Student Forum

Anything you would want to ask experts?

Write here...

Mensuration Formula, Definition, Rules, Sample Questions, Tips and FAQs

What is Mensuration?

Mensuration Formulas

Illustrated Examples of Mensuration Formulas

CAT Quantitative Aptitude Questions for Practice with Solutions

FAQs Related to Mensuration and Mensuration Formulas

MBA exams you must check out

Exams for which registrations will start soon

VEE

News & Updates

AIBE XIX (19) 2024: Check Exam Day Guidelines, Reporting & Bell Time, Difficulty level & Live Updates

AIBE 19 परीक्षा 2024: दिशा-निर्देश, ड्रेस कोड, केंद्र विवरण, महत्वपूर्ण क्या करें और क्या न करें

AIBE XIX (19) Answer Key 2024 (Awaited) Live Updates: Download Provisional Answer Key @allindiabarexamination.com

Last 15 years AIBE Question Papers With Answers free PDF Download

AIBE 19 Exam 2024: BCI Releases Important AIBE 19 Exam Day Guidelines

Landmark Judgements & Important Cases for AIBE 19 Preparation 2024

JEE Main Marks vs Percentile vs Rank 2024: Calculate Percentile and Rank Using Marks

NEET Chapter Wise Weightage 2025 PDF by NTA: Physics, Chemistry & Biology

CBSE 10th Maths Question Paper 2024, 2023, 2022, 2020, 2019 PDF Download

TET 2024: Notification, Exam Date, Admit Card, Syllabus, Eligibility & Results

Student Forum