Vipra ShrivastavaSenior Manager - Content
Probability is an integral part of the Maths syllabus of MBA entrance exams and other various competitive exams. You may well have explored Probability in school as an idea of chance - a measurement of the uncertainty of different phenomena. Here, a summary of Probability is given along with some sample questions and PDFs, focused on the Maths syllabus of higher classes, that will help you to quickly learn the relevant terms and also to achieve good marks in the CAT and other MBA entrance exams.
Probability: Mutually Exclusive Events
An occurrence is an effect or a blend of results of an experiment. Suppose we throw a die at you. Let E be the perfect square number case, then the answer is E = {1,4}. Whenever a result follows the criteria given in the scenario, we state that the incident has happened.
It is possible to expand the concept of mutually incompatible events to more than two events as well. More than two occurrences are mutually incompatible if the presence of one of them leaves out the occurrence of all other occurrences. In accordance with the experiment of tossing a single die, events A = {1, 2}, B = {3} and C = {6} are mutually exclusive. We will review what are mutually exclusive occurrences of probability in this portion.
Also Read: MBA Preparation: Tips to Prepare for MBA Entrance Exams
Probability Rules for Mutually Exclusive Events
Two instances are mutually exclusive or are disjointed informal logic if they do not occur simultaneously. Both findings are significant action when flipping the coin, which means that at least one of the results must happen since all the options are collectively exhausted by these two possibilities.
Probability laws are derived from the idea of mutually exclusive events.
- Law of Addition: P (A + B) = 1
- Law of Subtraction: P (A U B)' = 0
- Law of Multiplication: P (A x B) = 0
There are various forms of accidents as well. If the sample space of such an experiment is checked, it is either {H} for the first coin, or {T} for the second coin.
Conditional Probability for Mutually Exclusive Events
It is stated as the probability of an event A, provided that another event B has occurred. The conditional probability is denoted by the expression P(B|A) for two independent events B has given A and is defined using the equation
P(B|A)= P (A ∩ B)/P(A)
Using the multiplication rule to redefine the following equation: P (A ∩ B) = 0
P(B|A)= 0/P(A)
So, for mutually exclusive cases, the conditional probability formula is:
P (A | B) = 0
Illustrated Examples of Probability
Q 1: What is the probability of a die showing a number 3 or number 5?
Solution: Let,
P(3) is the probability of getting a number 3
P(5) is the probability of getting a number 5
P(3) = 1/6 and P(5) = 1/6
So,
P(3 or 5) = P(3) + P(5)
P(3 or 5) = (1/6) + (1/6) = 2/6
P(3 or 5) = ⅓
Therefore, the probability of a die showing 3 or 5 is 1/3.
Q 2: What is the probability of a dice showing a 2 or 5?
Solution: Let,
P(2) = 1/6
P(5) = 1/6
P(2 or 5) = P(2)+P(5)
= (1/6)+(1/6)
= ⅓
Q 3: A coin is tossed three times, consider the following events.
A: No tail appears
B: Exactly one tail appears
Do they form a set of mutually exclusive events?
Solution: The sample space S = { HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
A = {HHH}
B = { THH, HTH, HHT}
A⋂ B = Ø
Hence A and B are mutually exclusive events.
What is Random Variable?
The outcome of any particular event or experiment is a single real number which varies with the different outcomes. Let us assume that a cricket match is a random experiment and the number of wickets is the random variable that carries a numerical value. The value of the random variable X is expressed in terms of a real number. Thus, a real-valued function whose domain is the sample space of a random experiment.
Explanation of Random Variable
Suppose, a person tosses a coin twice in succession. The sample space of the event is S= {HH, HT, TH, TT}. If X is a random variable which denotes the number of heads obtained, the value of the random variable will be as follows: X (H, H) =2, X (H, T) =1, X (T, H) =1 and X (T, T) =0.
There can be another random variable Y for the same sample space S.
Probability Distribution of a Random Variable
A description giving the values of the random variable along with the corresponding probabilities is called the probability distribution of the random variable X.
| X |
X1 |
X2 |
………… |
Xn |
| P(X) |
P1 |
P2 |
………… |
Pn |
Where, Pi>0 and ΣPi= 1 and i= 1,2,3…. n.
Mean of a Random Variable
- The mean of the random variable X whose possible values may be x1, x2…xn, and their respective probabilities be p1, p2…pn is denoted by µ. It is the weighted average of the possible values of the random variable X. The mean is also known as the expectation of the random variable X denoted by E(X).
The Variance of a Random Variable
- For a random variable X, with values x1, x2…xn and their respective probabilities are p1, p2…pn and their mean µ=E(X), the variance is expressed as follows:
Var(X) or σ2x = (Xi-µ)2 *(p)*(xi)
= E(X-µ)2
Also Read:
| VARC Preparation Tips for MBA Exams | DILR Preparation Tips for MBA Exams |
Illustrated Examples of Random Variable
(from NCERT)
Q 1: A person plays a game of tossing a coin thrice. For each head, he is given Rs 2 by the organiser of the game and for each tail, he has to give Rs 1.50 to the organiser. Let X denote the amount gained or lost by the person. Show that X is a random variable and exhibit it as a function on the sample space of the experiment.
Solution: The sample space of the experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Then X (HHH) = Rs (2 × 3) = Rs 6
X(HHT) = X (HTH) = X(THH) = Rs (2 × 2 − 1 × 1.50) = Rs 2.50
X(HTT) = X(THT) = (TTH) = Rs (1 × 2) – (2 × 1.50) = – Re 1 and
X(TTT) = − Rs (3 × 1.50) = − Rs 4.50.
Where the minus sign shows the loss to the player where {–1, 2.50, – 4.50, 6}
Q 2: Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
Solution: The sample space of the experiment consists of 36 elementary events in the form of ordered pairs (xi, yi), where xi = 1, 2, 3, 4, 5, 6 and yi = 1, 2, 3, 4, 5, 6.
The random variable X i.e., the sum of the numbers on the two dice takes the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, or 12.
The probability distribution is:
Therefore,
μ = E(X) = Σ Xi*Pi = = 7.
Thus, the mean of the sum of the numbers that appear on throwing two fair dice is 7.
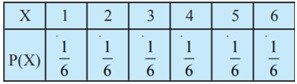
Q 3: Find the variance of the number obtained on a throw of an unbiased die.
Solution: The sample space of the experiment is S = {1, 2, 3, 4, 5, 6}. Let X denote the number obtained on the throw. Then X is a random variable that can take values 1, 2, 3, 4, 5, or 6.
E(X)= 1*1/6+2*1/6+2*1/6*4*1/6+5*1/6+6*1/6= 21/6
E(X2) = 12*1/6+22*1/6+32*1/6*+42*1/6+52*1/6+62*1/6= 91/6
Thus, Var (X) = E (X2) – (E(X))2= 35/12.
Read More:
CAT Quantitative Aptitude Practice Questions with Solutions
Get here sample questions and practice tests of how to prepare for Quantitative Aptitude for CAT pdf with solutions for practice.
Download more Free PDFs of Quantitative Aptitude Sample Questions and Answers for Practice
FAQs Related to Probability
Q: Do mutually exclusive events add up to 1?
Q: How do you do mutually exclusive problems?
Q: Can two events be dependent and not mutually exclusive?
Q: What is the formula for non mutually exclusive events?
Q: How do you know if something is mutually exclusive?
Q: What are the different types of random variables?
Q: What is the sum of probabilities for all the possible values of a discrete random variable X?
Q: What are the few examples of a discrete random variable?
Q: Which two conditions should be satisfied for the probability Pi of a random variable value X?
Q: What is the distribution function of all random variables?
Q: Can the mean of a random variable be negative?
News & Updates
Quantitative Aptitude Prep Tips for MBA Exam