Salviya AntonySenior Executive - Content
Faraday's law refers to two fundamental principles in the field of electromagnetism, formulated by the British scientist Michael Faraday in the early 19th century. These principles are integral to our understanding of how electricity and magnetism are related. Faraday’s law, is also called Faraday’s law of electromagnetic induction. It is the basic law of electromagnetism which explains how a magnetic field would interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is called electromagnetic induction.
Faraday’s law is the observation or results of the experiments conducted by Michael Faraday. He conducted three main experiments to find the phenomenon of electromagnetic induction. In NCERT Class 12 Chemistry, Faraday's law is an important topic. Students lear this topic in chapter Electrochemistry.
Faraday's First Law of Electromagnetic Induction
This law states that a change in magnetic field within a closed loop of wire induces an electromotive force (EMF) in the wire. In other words, when the magnetic field passing through a loop of wire changes, it causes an electric current to flow in the wire. This law is the basis for the operation of generators, which convert mechanical energy into electrical energy by changing magnetic fields.
Faraday's Second Law of Electromagnetic Induction
This law quantifies the relationship between the rate of change of magnetic flux and the induced EMF. It states that the magnitude of the induced EMF is directly proportional to the rate of change of magnetic flux through the circuit. Mathematically, it is expressed as:
EMF = -dΦ/dt
Where EMF is the electromotive force (voltage), dΦ/dt is the rate of change of magnetic flux, and the negative sign indicates that the induced EMF produces a current that opposes the change in magnetic flux (this is known as Lenz's Law).
These two laws are crucial in understanding the operation of transformers, electric generators, and other electromagnetic devices. Faraday's work laid the foundation for our understanding of how electrical energy can be generated, transmitted, and used in various applications, forming the basis for modern electrical engineering and technology.
Lenz’s Law
Lenz’s law states that the polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produced it.
Lenz's law formula is given by
Emf = -N(Δφ/Δt)
Emf is the induced voltage (also known as electromotive force).
N is the number of loops.
Δφ is the change in magnetic flux
Δt is the change in time.
The negative sign shows that the direction of the induced emf and the change in the direction of magnetic fields have opposite signs.
Faraday’s Law Derivation
Consider an experiment in which a magnet approaching a coil. Let T1 and T2 be the two-time instances.
Flux linkage with the coil at the time T1 = NΦ1.
Flux linkage with the coil at the time T2 = NΦ2
Change in the flux linkage = N(Φ2 – Φ1)
Let change in flux linkage is Φ = Φ2 – Φ1
Therefore the change in flux linkage = NΦ
The rate of change of flux linkage = NΦ/t
Taking the derivative we get
N dΦ/dt
From Faraday’s second law of electromagnetic induction, we know that the induced emf in a coil is equal to the rate of change of flux linkage.
Hence, E = N dΦ/dt
Considering Lenz's law, E = - N dΦ/dt
We can conclude that, when the number of turns in the coil increases, the induced emf increases.
When the magnetic field strength increases, the induced emf increases.
Increasing the speed of the relative motion between the coil and the magnet, leads to the increased emf
Faraday's Law: Applications
- Transformers works on the principle of electromagnetic induction
- Induction motor ia an application of Faraday's law
- An induction furnace used in the kitchen
- Electrical generators works on the principle as electro magnetic induction.
- Tape recorders works on the principle of electromagnetic induction.
FAQs on Faraday's Law
Q: How much charge is required for the following reductions: (i) 1 mol of Al3+ to Al? (ii) 1 mol of Cu2+ to Cu? (iii) 1 mol of MnO4 – to Mn2+ ?
A: The electrode reaction is given as,
Al3+ (aq) + 3e- → Al(s)
∴ The quantity of charge required for the reduction of 1 mol of Al3+ = 3F
= 3×96487 C
= 289461 C
The electrode reaction is given as,
Cu2+ (aq) + 2e- → Cu(s)
∴ The quantity of charge required for the reduction of 1 mol of Cu2+ = 2F
= 2×96487 C
= 192974 C
The electrode reaction is given as, MnO4→ Mn2+
i.e., Mn7+ + 5e - → Mn2+
∴ The quantity of charge required for the reduction of 1 mol of Mn7+ = 5F
= 5×96487 C
= 482435 C
Q: How much electricity in terms of Faraday is required to produce (i) 20.0 g of Ca from molten CaCl2?
A: (i) Ca2+ + 2e- → Ca
⇒ Here, 1 mole of Ca, i.e., 40g of Ca requires = 2 F electricity (F if Faraday)
∴ 20g of Ca requires = 20X2/40
= 1 F of electricity
Electricity in terms of Faraday required to produce 20.0 g of Ca from molten CaCl2 is 1 F of electricity.
(ii) Al3+ + 3e- → Al
⇒ 1 mole of Al, i.e., 27g of Al requires = 3 F electricity (F if Faraday)
∴ 40.0 g of Al will require = 3/27 X 40
= 4.44 F of electricity
Electricity in terms of Faraday required to produce 40.0 g of Al from molten Al2O3 is 4.44 F of electricity.
Q: How much electricity is required in coulomb for the oxidation of (i) 1 mol of H2O to O2 ? (ii) 1 mol of FeO to Fe2 O3 ?
A: The electrode reaction for 1 mole of H2O is given as,
H2O → H2 + 1/2O2
i.e., O2- →1/2 O2 + 2e -
∴ The quantity of electricity required = 2F
= 2×96487 C
= 192974 C
The quantity of electricity required in coulomb for the oxidation of 1 mol of H2O to O2 is 192974 C
- (ii) The electrode reaction for 1 mole of FeO is
FeO + 1/2 O2 → 1/2 Fe2O3
i.e., Fe2+ → Fe3+ + e -
∴ The quantity of electricity required = 1F
= 1×96487 C
= 96487 C
The quantity of electricity required in coulomb for the oxidation of 1 mol of FeO to Fe2O3 is 96487 C
Q: A solution of Ni(NO3)2 is electrolysed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?
A: Quantity of electricity passed = 5 A × (20 × 60 sec)
= 6000 C ⇒ Equation 1
The electrode reaction is written as,
Ni2+ + 2e → Ni
Thus, the quantity of electricity required = 2F
= 2×96487 C
= 192974 C
∵ 192974 C of electricity deposits 1 mole of Ni, which is 58.7 g ⇒ Equation 2
Thus, equating equations 1 and 2, we get
192974 C of electricity deposits = 58.7 g
6000 C of electricity will deposit = 58.7 X 6000 / 192974
= 1.825g of Ni
The mass of Ni deposited at the cathode is 1.825g of Ni
Q: Three electrolytic cells A, B, C containing solutions of ZnSO4 , AgNO3 and CuSO4 , respectively are connected in series. A steady current of 1.5 amperes was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?
A: Equivalent weight is Ag, EAg = 180/1 = 180
Equivalent weight is Cu, ECu = 63.5 / 2 = 31.75
Equivalent weight is Zn, EZn= 65/2 = 32.5
Using Faraday’s second law of electrolysis, to find the mass of Cu and Zn, we use Equation 1,
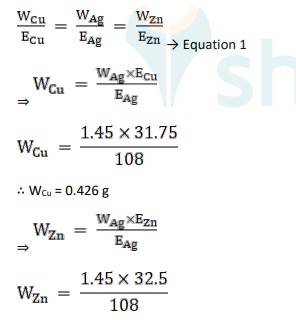
∴ WZn = 0.436 g
To find the time of current flow, using Faraday’s first law of electrolysis we get,
M = Z ×I ×t ⇒ Equation 2
∵ Z = Equivalent Weight / 96487 , Equation 2 becomes,
M = 108 / 96487 X 1.5 X t
t = 1.45 X 96487 / 108X 1.5
t = 864 seconds.
The time of current flow, t = 864 seconds, the mass of Cu is 0.426 g and mass of Zn is 0.436 g
News & Updates
Atoms and Molecules Exam
Student Forum
Anything you would want to ask experts?Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test