Salviya AntonySenior Executive - Content
Vapour Pressure refers to the pressure exerted by the vapour (gas phase) of a substance in equilibrium with its liquid or solid phase at a given temperature. This phenomenon occurs in closed containers where molecules from the liquid or solid phase continuously evaporate into the gas phase and condense back into the liquid or solid phase.
We define vapour pressure as the pressure exerted by the vapour present above the liquid. Temperature is an important factor that affects vapour pressure. The vapour pressure of a liquid is independent of the volume of liquid in the container. When the temperature increases, the vapour pressure also increases. Vapour pressure is an important topic in NCERT Class 12 Chemistry. Students will Vapour pressure of liquids in NCERT Class 12 Chemistry Chapter 2 Solutions.
Vapour Pressure: Important Points
Temperature Dependence:
Vapour pressure is highly temperature-dependent. As the temperature increases, the kinetic energy of the molecules also increases. Consequently, more molecules have sufficient energy to break away from the liquid or solid phase and enter the gas phase, leading to an increase in vapour pressure. Conversely, as the temperature decreases, vapour pressure decreases.
Liquid Phase Equilibrium:
When a liquid is placed in a closed container, the rate of evaporation equals the rate of condensation when equilibrium is reached. At this point, the vapour pressure remains constant, and the system is said to be in a dynamic equilibrium.
Boiling Point:
The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the atmospheric pressure. At this temperature, bubbles of vapour form throughout the liquid, and it begins to boil.
Intermolecular Forces:
The strength of intermolecular forces between molecules in a substance can affect its vapour pressure. Substances with weaker intermolecular forces tend to have higher vapour pressures at a given temperature because their molecules can more easily escape into the gas phase.
Raoult’s law:
In general form this law can be stated as, for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
Applications of Vapour Pressure
Understanding vapour pressure is essential in various practical applications, including cooking (boiling point of water), chemistry experiments, and the operation of engines (fuel vapourization). Additionally, vapour pressure plays a critical role in atmospheric science and the behaviour of volatile organic compounds in the environment.
FAQs on Vapour Pressure
Q: An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
A:
given:
2% non-volatile solute in an aqueous solution means that if the solution is of mass 100 g then the mass of solute in the solution is,
Mass of solute = [2 × 100]/100
= 2 g
∴ Mass of Solvent = 100-2
= 98 g
Vapour pressure of solution at normal boiling point, P1 = 1.004 bar
Vapour pressure of pure water at normal boiling point, P1° = 1 atm = 1.013 bar
To find: Molar mass of solute
Formula:
From Raoult’s Law, we have:
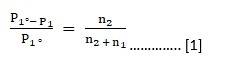
Now we know that number of moles of solute is given by the following relationship,
⇒ Number of moles = Mass of solute / Molecular mass of solute
Using the above relationship the equation [1] can be modified as follows:
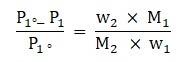
Where
W1 = mass of solvent
W2 = mass of solute
M1 = molecular mass of solvent
M2 = molecular mass of solute
Solution:
(1.013 - 1.004) / 1.013 = 2 X 18 / 98 X M2
0.009 / 1.013 = 36 / 98M2
M2 = 36 X 1.013 / 98 X 0.009
M2 = 41.3469 g
∴ M2 ≈ 41.35 g
Therefore the molar mass of the solute is 41.35 g.
Q: Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure of a mixture of 26.0 g of heptane and 35 g of octane?
A: Given: Temperature = 373k
Vapour pressure of pure heptane (p10 ) = 105.2 kpa and that of octane (p20 ) = 46.8 kpa
Mass of heptane = 26 g
Mass of octane = 35 g
Molecular weight of heptane = C7H16 = 12 × 7 + 1 × 16 = 100 gmol-1
Molecular weight of octane = C8H18 = 114 gmol-1
Moles of heptane, n1 = given mass /molecular weight = 26/100
⇒ n1 = 0.26mol
Moles of octane, n2 = given mass /molecular weight = 35/114
⇒ n2 = 0.307mol
∴ Partial pressure of heptane, p1 = χ1 × p10
⇒ p1 = 0.456 × 105.2 = 47.97kpa
∴ Partial pressure of octane, p1 = χ2 × p20
⇒ p2 = 0.544 × 46.8 = 25.46 kpa
∴ Total pressure exerted by solution = p1 + p2
= 47.97 + 25.46
= 73.43 kpa
Q: The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
A:
Given: 1 molal solution means 1 mole of solute present in 1000g of water solvent)
Molecular weight of water = H2O = 1 × 2 + 16 = 18g/mol
No. of moles of water, n = given mass /molecular weight
⇒ n = 1000/18 = 55.56 gmol-1
Mole fraction of solute in solution,x2 = moles of solute/(moles of solute + moles of water)
⇒ x2 = 1/(1 + 55.56)
⇒ x2 = 0.0177
Given vapour pressure of pure water at 300k is 12.3 kpa
Apply the formula:
⇒ P1 = 12.0823kpa
which is the vapour pressure of the solution.
Q: Calculate the mass of a non-volatile solute (molar mass 40 g mol^–1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
A:
Given:
Molar mass of non-volatile solute = 40g
Let no. of moles of solute be n.
Mass of octane = 114g
Molar mass of octane(C8H18) = 12 × 8 + 1 × 18 = 114g/mol
Moles of octane = given mass/molar mass
⇒ n = 114/114 moles
⇒ n = 1 mole
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
⇒ x2 = n/n + 1
Let the vapour pressure of original solvent(without solute) be p1⁰
Accordingly after addition of solute vapour pressure of solution reduces to 80% i.e.
0.8 p1⁰ = p1
Applying the formula:
⇒ n/n + 1 = 0.2
⇒ 0.2n + 0.2 = n
⇒ n = 0.25 moles
Hence, mass of solute is:
moles = given mass/molar mass
⇒ 0.25moles = mass/40g
⇒ mass = 10g.
Q: A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further, 18 g of water is then added to the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate: (i) molar mass of the solute (ii) vapour pressure of water at 298 K.
A:
Given: mass of solute = 30g
Let the molar mass of solute be x g and vapour pressure of pure water at 298k be P1 ⁰
Mass of water(solvent) = 90g
Molar mass of water = H2O = 1 × 2 + 16 = 18g
Moles of water = mass of water/molar mass
⇒ n = 90/18 moles
⇒ n = 5moles
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
x2 = (30/x) / (30/x) + 5
x2 = 30 / 30+5x
Vapour pressure of solution (p1) = 2.8kpa
Applying the formula:
According to second condition when we add 18g of water to solution vapour pressure becomes 2.9kpa
Moles of water = mass/molar mass
⇒ n = 90 + 18/18
⇒ n = 6moles
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
x2 = (30/x) / (30/x) + 6
x2 = 30 / 30+6x
Applying the formula:
Solving 1 and 2:
Dividing (2) by (1) we get
(i) molar mass of the solute = 78g
(ii) vapour pressure of water at 298 K = 537kpa
News & Updates
Atoms and Molecules Exam
Student Forum
Anything you would want to ask experts?Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test