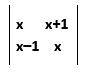Determinants: Overview, Questions, Preparation

A matrix is a definite set of objects that is organised in rows as well as columns. These objects are called components of the Matrix. The classification of a matrix is written as number rows by several columns. In simple words, a matrix is an array of many numbers.

Kinds of Matrices

There are various kinds of matrices.

Zero Matrix: A matrix whose all components are zero is known as a null matrix. The general sense of null is nothing that means zero.

Identity Matrix: It's a square matrix with all the entries zero, except for the entries on the central diagonal (upper left to lower right), which are 1.

Symmetric Matrix: Matrix is symmetric if the m-th row and n-th column element are equal to the n-th row and the mm-th column components. You could say the rows of a symmetric matrix are always the same as the columns.

Diagonal Matrix: A diagonal matrix is a kind of Matrix in which diagonal elements are non-zero and non-diagonal elements are zero.

Upper Triangular Matrix: It is considered a square matrix in which all the elements below the main diagonals are 0.

Lower Triangular Matrix: It is considered a square matrix in which all the elements above the main diagonal are 0. The definition is silent about the factor below the main diagonal.

Determinants are mathematical objects that are very beneficial in the study and solution of systems of linear equations. A determinant of Matrix denotes a singular number. We get this number by multiplying plus summing its elements in a particular method. Generally, a determinant is a square arrangement of numbers (written in a vertical line array) representing a definite sum of products.

Example: 4×7− 9×5 = 28 − 35 = −17

Properties of determinants

There are several attributes of determinants, particularly the conversion of the row and column conversions, that can interpret the evaluation of any determinant significantly:

Property 1: The determinant's value is unchanged when rows switch into columns and columns into rows.

Property 2: When two rows or columns of a determinant reciprocates, the sign of the determinant changes. However, its magnitude continues alike.

Property 3: A determinant having two rows or two columns identical has the value of zero

Property 4: Multiplying all the elements of a row (or column) by a scalar (a real number) is equal to multiplying the scalar's determinant.

Property 5: A determinant sorts into a sum of two determinants along any row or column.

This concept is taught in chapter Determinants. The weightage of this chapter is 6 marks.

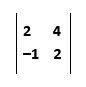
1.Evaluate 

Solution.
= 2(2) – 4(–1) = 4 + 4 = 8.

2. Evaluate

Solution.

x (x) – (x + 1) (x – 1) = x² – (x² – 1) = x² – x² + 1 = 1

3. Evaluate

= 4 (–1 – 12) – 0 + 0 = – 52

Q: What is a matrix?

Q: What is a square matrix?

Q: What are determinants?

Q: What are the objectives of a determinant of a matrix?

Q: What is the formula of determinant?