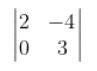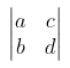Cofactor: Overview, Questions, Preparation

In a matrix, the number obtained when denoting a minor with a proper sign is called a cofactor. A minor can be computed by deleting the column and row where a particular element is situated. Cofactor of an element a_ij, is depicted by A_ij, whereas the minor is presented as Mij.
i.e., A_ij=(-1)^i+j x M^ij, 

Cofactors are introduced to students in the chapter, Determinants in grade 12. The CBSE board gives a weightage of 10 marks for the whole unit Algebra, under which this topic is discussed. Cofactors are used in calculating the adjoints and inverses of matrices.

When the row or column elements are multiplied with any other row or column’s cofactors, their sum is equal to zero.

1. Write minors and cofactors of the elements of the following determinant:

Solution.

The minors for this determinant are obtained by crossing out the column and row in which that particular element is situated. Therefore,
M₁₁= 3
M₁₂= 0
M₂₁=-4
M₂₂= 2
The corresponding cofactors are found using the equation, Aij=(-1)i+jMij
A₁₁=(-1)¹⁺¹ x 3= 3
A₁₂=(-1)¹⁺² x 0= 0
A₂₁=(-1)²⁺¹ x -4= 4
A₂₂=(-1)²⁺² x 2= 2

2. Write minors and cofactors of the elements of the following determinant:

Solution.

The minors for this determinant are:
M₁₁= d
M₁₂= b
M₂₁= c
M₂₂= a
The cofactors for this determinant are:
A₁₁=(-1)¹⁺¹ x d = d
A₁₂=(-1)¹⁺² x b = -b
A₂₁=(-1)²⁺¹ x c = -c
A₂₂=(-1)²⁺² x a =  a

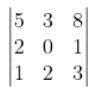
3.Using cofactors of elements of the second row, evaluate Δ= 

Solution.

M₂₁= 

 =9-16=-7

∴ Cofactor of  a₂₁, A₂₁=(-1)²⁺¹ x -7=7

M₂₂= 

=15-8=7
∴ Cofactor A₂₂=(-1)²⁺² x 7=7

M23= 

 =10-3=7
∴ Cofactor A₂₃=(-1)²⁺³ x 7=-7

A determinant, Δ is equal to the sum of the product of the second-row elements with their corresponding cofactors. In this case the determinant, 
Δ= a₂₁A₂₁+a₂₂A₂₂+a₂₃A₂₃
=27 + 07 + 1(-7)= 7.

Q: What are the applications of cofactors?

Q: Differentiate between cofactors and minors of a matrix.

Q: Is there any method to verify whether the cofactor calculated is correct or not?

Q: What determines the sign in cofactor?

Q: Is it possible to evaluate a determinant Δ, using cofactors?