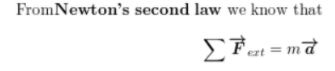- What is Newton's Law of Motion?
- Newton's First Law (Law of Inertia)
- Newton's Second Law
- Newton's Third Law
- Illustrative Examples
- FAQs on Newton's Law of Motion
What is Newton's Law of Motion?
Newton's Law of Motion exhibits a relationship between the body and the forces acting on it. This force causes a change in the motion. Sir Issac Newton laid the foundation of mechanics in terms of three laws of motion.
Newton's Laws of Motion
Newton's First Law (Law of Inertia)
Every body continues to be in its state of rest or uniform motion in a straight line unless compelled by some external force to act otherwise. So, if the net external force on a body is zero, its acceleration is zero.
Example
Consider a book at rest on a horizontal surface. It is subjected to two external forces, the force due to gravity (weight W) acting downward and upward force (R) on the book by the table. If the force on the object is equal and opposite, they are said to be balanced. Since the book is at rest, the net force is zero, which implies that force R must be equal and opposite to W.
Newton's Second Law
The rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction in which the force acts.
Example
If two stones, light and heavy, are dropped from the top of a building, a person on the ground will find it easier to catch the light stone than the heavy stone. The greater the speed, the greater the opposing force needed. Thus the mass and speed of the body is an important parameter that determines the effect of force on its motion.
Under the action of force F for time interval Δt, the velocity of the body of mass m changes from v to v+Δv. So initial momentum p=mv changes to Δp =mΔv.
Newton's Third Law
To every action, there is always an equal and opposite reaction.
Action and reaction forces act on different bodies, not on the same body. Consider a pair of bodies A and B. According to the third law, FAB = – FBA
Example
Newton's Laws of Motion for Class 11
Laws of Motion is the most important chapter. Questions will be on Newton's laws of motion, its examples, applications and problems based on the force, momentum and acceleration. The weightage of the topic is 10 marks.
Illustrative Examples
1. A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m/s. How long does the body take to stop?
Solution: F= -50 N(retardation force), m = 20 kg
a = F/m = -50/20 = -2.5ms⁻²
v = u +at ; u = 15, v =0, a= -2.5
t = -15/-2.5 =6s
2. A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0ms⁻². Calculate the force of the blast.
Solution: M= 20000 kg = 2×10⁴ kg, a = 5
The thrust should overcome the force of gravity besides giving it an upward acceleration.
g= 9.8
F = m(a+g) = 2×10⁴(5+9.8) =2.96 ×10⁵ N
3. Anmol, a 55 kg sprinter, starts with an acceleration of 3.5 m/s². What will be the net external force?
Solution: F = 55× 3.5 = 192.5N
FAQs on Newton's Law of Motion
Q: One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards the centre) is: (i) T, (ii) T - (mv^2)/l (iii) T + (mv^2)/l (iv) 0 T is the tension in the string. [Choose the correct alternative].
A: The net force acting on the string is the tension of the string, no other forces. Hence the answer is T.
Q: A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m s-1. How long does the body take to stop?
A: The retarding force, F = 50N, the mass m = 20 kg From the equation F = ma, we get acceleration a = 50 / 20 m/s2 = 2.5 m/s2 The initial speed , u = 15 m/s, the final speed v =0, from the relation v = u-at, we get t = u/a = 15/2.5 s = 6s
Q: A constant force acting on a body of mass 3.0 kg changes its speed from 2.0 m s^-1 to 3.5 m s^-1 in 25 s. The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?
A: Initial speed, u = 2.0 m/s, the final speed v = 3.5 m/s, the time t = 25 s From the relation v = u + at, we get acceleration a = (v-u)/t = (3.5 – 2.0 )/ 25s = 0.06 m/s2 The force F = ma, F = 3 X 0.06 N = 0.18 N
Q: What happens according to Newton if you let an untied balloon go?
A: Air will rush out of the balloon forcing the balloon to move through the air in the opposite direction, but equal in force (third law).
Q: How do Newton’s laws affect your daily life?
A: Everything that happens in our lives is connected to Newton's law of motion since force is involved in everything.
Q: What is required to cause acceleration?
A: An unbalanced force (or non-zero net force) is needed to cause acceleration.
Q: Inertia is the resistance to change in motion, so inertia depends solely on what?
A: Mass
Q: Is Newton's third law always true?
A: No, magnetic forces do not obey the third law.
Physics Laws of Motion Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test