Salviya AntonySenior Executive - Content
NCERT Class 11 Chemistry chapter Structure of Atom is a favorite topic among chemistry lovers. It dwells into the basics structure and components of atoms i.e., electrons, protons and neutrons, the arrangement of nucleus and various laws governing the constitution of nucleus.
The chapter Structure of atom covers many topics that are important in boards as well as entrance exams like JEE Main, MHT CET and others. Students can check here NCERT class 11 Chemistry structure of atom solution to score good marks in the exam. Those preparing for entrance exams can refer NCERT Solutions Chemistry class 12.
NCERT Chemistry Class11th Structure of Atoms Chapter Topics Covered
Various topics covered in this chapter are
- Sub-atomic Particles
- Discovery of Electrons
- Discovery of Protons and Neutrons
- Atomic Models
- Thomson Model of Atom
- Rutherford’s Nuclear Model of Atom
- Atomic Number and Mass Number
- Isobar and Isotopes
- Development of Bohr’s Atomic Model
- Wave Nature of Electromagnetic Radiation
- Particle Nature of Electromagnetic Radiation
- Photoelectric Effect
- Bohr’s Model for Hydrogen Atom
- Quantum Mechanical Atom of Atom
- Heisenberg’s Uncertainty Principle
- Orbitals and Quantum Numbers
- Shapes of Atomic Orbitals
- Energies of Atomic Orbitals
- Filling of Orbitals in Atoms
- Pauli Exclusion Principle
- Afbau Principle
- Stability of Completely Filled and Half Filled Subshells
NCERT Chemistry Class11th Solution PDF for Structure of Atoms
Student are provided here NCERT solution class 11 chemistry structure of atom to help make their learning of this chapter more fun and easy to understand. The solution of this chapter has been prepared by expert teachers and subject matter experts. Chemistry NCERT Class 11th Structure of Atom chapter covers various topics like discovery of electron, proton and neutron, Atomic models like Thomson and Rutherford model of atom, their drawbacks leading to the development of Bohr’s atomic models, isobars and isotopes and others.
Download Here: NCERT Class 11th Solution for Chemistry Structure of Atom PDF
Structure of Atoms Additional Questions
2.1. Assertion: Rainbow is a line spectrum.
Reason: In rainbow, the violet merges into blue, blue into green and so on.
Answer: (d) Rainbow is a continuous spectrum.
Assertion is a wrong statement but Reason is a correct one. Rainbow is a continuous spectrum.
2.2. Assertion: Classical mechanics fails when applied to microscopic objects like electrons, atoms, molecules etc.
Reason: Classical mechanics ignores the concept of dual behaviour of matter especially for sub-atomic particles and the uncertainty principle.
Answer: (a) Classical mechanics applies to the macro world and hence fails when it is applied to the micro worlds. In the micro world, quantum mechanics incorporates all the principles like the uncertainty principle, dual behaviour etc.
2.3. Assertion: Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously (Heisenberg uncertainty principle).
Reason: The path of an electron in an atom can be determined accurately.
Answer: (c) The path of an electron in an atom can never be determined or known accurately. That is why; there is only probability of finding the electron at different points in an atom.
2.4. Assertion: Chromium and copper have five and ten electrons in 3d orbitals rather than four and nine as their position would have indicated with two-electrons in the 4s orbital.
Reason: Fully filled and half-filled orbital shave extra stability that is, lower energy.
Answer: (a) Fully filled and half-filled orbitals have extra stability (that is, lower energy). Thus, p3, p6, d5, d10, f 7, f14 etc. configurations, which are either half-filled or fully filled, are more stable. Chromium and copper therefore adopt the d5 and d10 configuration.
2.5. Assertion: Symmetrical distribution of electrons leads to stability.
Reason: Electronic distribution of an element is important to understand and explain the chemical behaviour of the element.
Answer: (b) Both the statements are correct but R is not the reason for A.
MCQs
2.1. Which one of the following statements is correct?
(a) Fe3+ is more paramagnetic than Fe2+.
(b) Fe2+ is more paramagnetic than Fe3+.
(c) Both are equally paramagnetic.
(d) They are non-magnetic.
Answer: (a) As Fe3+ contains 5 impaired electrons while Fe2+ contains only 4 unpaired electrons. Fe3+ is more paramagnetic.
2.2. Which element does not have any neutron?
(a) Li (b) C (c) H (d) B
Answer: (c) H
2.3. What is value of Planck’s constant in S.I. units?
(a) 6.62 x 1024 Js (b) 6.62 x 1034 Js (c) 6.62 x 10-24 Js (d) 6.62 x 10-34 Js
Answer: (d) 6.62 x 10-34 Js.
2.4. The energy needed to remove a single electron (most loosely bound) from an isolated – gaseous atom is called
(a) ionisation energy (b) electronegativity
(c) Kinetic energy (d) electron affinity
Answer: (a) ionisation energy
2.5. The maximum number of electrons in a sub-shell is given by the equation
(a) n2 (b) 2n2 (c) 2l – 1 (d) 2l + 1
Answer: (d) 2l + 1
Question Answer:
2.1. Why all isotopes of a given element show the same type of chemical behaviour?
Answer: The chemical properties of an atom are controlled by the number of electrons in the atom, which remains the same despite the change or variation in atomic masses in case the of isotopes.
2.2. State Heisenberg’s Uncertainty Principle and the significance of it.
Answer: Werner Heisenberg a German physicist in 1927, stated uncertainty principle which is the consequence of dual behaviour of matter and. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron.
It rules out existence of definite paths or trajectories of electrons and other similar particles.
2.3 Define a black body. Does a complete black body exist practically?
Answer: An ideal body, which emits and absorbs radiations of all frequencies uniformly, is called a black body and the radiation emitted by such a body is called black body radiation. In practice, no such body exists. Carbon black approximates fairly closely to black body. A good physical approximation to a black body is a cavity with a tiny hole, which has no other opening. Any ray entering the hole will be reflected by the cavity walls and will be eventually absorbed by the walls.
2.4. Differentiate between continuous spectra and atomic spectra.
Answer: Since ordinary white light consists of waves with all the wavelengths in the visible range, a ray of white light is spread out into a series of coloured bands called spectrum. The light of red colour which has longest wavelength is deviated the least while the violet light, which has shortest wavelength, is deviated the most.
The spectrum of white light, that we can see, ranges from violet at 7.50 × 1014 Hz to red at
4×1014 Hz. Such a spectrum is called continuous spectrum (Continuous because violet merges into blue, blue into green and so on). A similar spectrum is produced when a rainbow forms in the sky.
The emission spectra of atoms in the gas phase, on the other hand, do not show a continuous spread of wavelength from red to violet, rather they emit light only at specific wavelengths with dark spaces between them.
Such spectra are called line spectra or atomic spectra because the emitted radiation is identified by the appearance of bright lines in the spectra.
2.5. What is the most important application of de Broglie concept?
Answer: de Broglie concept has been put to use in making an electron microscope, which is based on the wavelike behaviour of electrons just as an ordinary microscope utilises the wave nature of light. An electron microscope is a powerful tool in modern scientific research because it achieves a magnification of about 15 million times.
2.6. Discuss the similarities and differences between a 1s and a 2s orbital.
Answer: Similarities:
• Both have spherical shape.
• Both have same angular momentum.
Differences:
• 1s has no node while 2s has one node.
• Energy of 2s is greater than that of 1s.
2.7. What were the weaknesses or limitations of Bohr’s model of atoms? Briefly describe the quantum mechanical model of atom.
Answer: Limitations of Bohr’s model of an atom:
• It could not explain spectrum of multi-electron atoms.
• It could not explain Zeeman and Stark effects.
• It could not explain shape of molecules.
• It was not in accordance with Heisenberg’s uncertainty principle.
Quantum Mechanical Model: It was developed on the basis of Heisenberg’s uncertainty principle and dual behaviour of matter.
Main features of this model are given below:
• The energy of electrons in an atom is quantized i.e. can only have certain values.
• The existence of quantized electronic energy levels is a direct result of the wave like properties of electrons.
• Both, the exact position and velocity of an electron in an atom cannot be determined simultaneously.
• The orbitals are filled in increasing order of energy. All the information about the electron in an atom is stored in orbital wave function Ψ.
• From the value of Ψ2 at different points within atom, it is possible to predict the region around the nucleus where electron most probably will be found.
Explore exams which ask questions on Ncert Solutions Chemistry Class 11th
Select your preferred stream
Structure of Atom Solutions and FAQs
Q 2.1. (i) Calculate the number of electrons which will together weigh one gram. (ii) Calculate the mass and charge of one mole of electrons.
A 2.1 (i) Mass of an electron = 9.10939×10−31 kg = 9.1 × 10-28 g
- No. of electrons in 9.1 × 10-28 g = 1 electron
- Therefore, No. of electrons in 1 g = 1/9.1 × 10-28 = 1.098×1027
(ii) One mole of electrons = 6.022 × 1023 electrons
- Mass of 1 electron = 9.1 × 10-31 kg
- Mass of 6.022 × 1023 electrons = (9.1 × 10-31kg) × (6.022 × 1023) = 5.48 × 10-7 kg
- Charge on one electron = 1.602 × 10-19 C
- Charge on one mole electrons = 1.602 × 10-19 × 6.022 × 1023 = 9.65 × 104 C
Q 2.2.(i) Calculate the total number of electrons present in one mole of methane. (ii) Find (a) the total number and (b) the total mass of neutrons in 7 mg of 14^C. (Assume that mass of a neutron = 1.675 × 10^-27kg). (iii) Find (a) the total number and (b) the total mass of protons in 34 mg of NH3 at STP. Will the answer change if the temperature and pressure are changed?
A 2.2 (i) One mole of methane (CH4) has = 6.022 × 1023 molecules
No. of electrons present in one molecule of CH4 = 6 + (4 x 1) = 10
No. of electrons present in 6.022 × 1023 molecules of CH4 = 6.022 × 1023 × 10
= 6.022 × 1024 electrons (ii) (a) Calculation of total number of carbon atoms
Gram atomic mass of carbon (C-14) = 14 g = 14 × 103 mg
14 g or 14 × 103 mg of carbon (C-14) has 6.022 × 1023 atoms No of neutrons on 1 atom of (C-14) = 14-6= 8 ⇒ No. of neutrons in 14g of (C-14) = 6.022× 1023 ×8 So, 7 mg of carbon (C-14) has = (6.022 × 1023 ×8) / (14 x 103 mg) x (7 mg) = 2.408 × 1021 neutrons
(b) Calculation of total number and total mass of neutrons
Mass of one neutron = 1.675 × 10-27 kg
Mass of 2.408 × 1021 neutrons = (1.675 x 10-27 kg) × 2.408 × 1021
= 4.033 × 10-6 kg (iii) (a) Calculation of total number ofNH3 molecules
Gram molecular mass of ammonia (NH3) = 17 g = 17 × 103 mg
17 × 103 mg of NH3 have molecules = 6.022 × 1023 34 mg of NH3 have molecules = (6.022 × 1023) / (17 x 103) x 34 mg = 1.2044 x 1020 molecules
(b) Calculation of total number and mass of protons
No. of protons present in one molecule of NH3 = 7 + 3 = 10
No. of protons present in 12.044 × 1020 molecules of NH3 = 12.044 × 1020 × 10
= 1.2044 × 1022 protons
Mass of one proton = 1.67 × 10-27 kg
Mass of 1.2044 × 1022 protons = (1.67 × 10-27 kg) × 1.2044 × 1022
= 2.01 × 10-5 kg Since, the mass and number of protons is independent of the temperature and pressure conditions. So, there will no change in the answer upon changing the temperature and pressure because only the number of protons and mass of protons are involved.
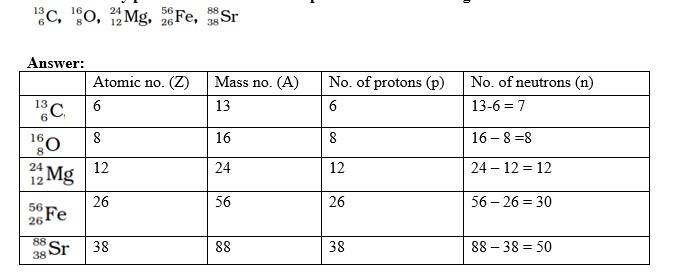
Q 2.3. How many protons and neutrons are present in the following nuclei
A 2.3
Q 2.4.Write the complete symbol for the atom (X) with the given atomic number (Z) and atomic mass (A) (i) Z = 17,A = 35 (ii) Z = 92, A = 233 (in) Z = 4, A = 9
A 2.4
Q 2.5. Yellow light emitted from a sodium lamp has a wavelength (λ) of 580 nm. Calculate the frequency (ν) and wavenumber (ṽ) of the yellow light. A
A 2.5 Using the formula, frequency = speed of light/wavelength Or, ν = c/λ , where c = 3 x 108 ms-1 and λ = 580 nm (given) = 580 x 10-9 m Therefore, frequency ν = 3 x 108 ms-1 / 580 x 10-9 m = 5.17 x 1014 s-1 Wavenumber (ṽ) = = 1/ 580 x 10-9 m = 1.724 x 106 m-1
Q 2.6.Calculate the energy of each of the photons which (i) correspond to light of frequency 3 × 10^15 Hz (ii) have wavelength of 0.50 Å.
A 2.6 (i) Energy of photon (E) = hν, where h= Plank’s const, ν= Frequency
h= 6.626 × 10-34 J s ; ν = 3 × 1015 Hz = 3 × 1015 s-1
∴ E = (6.626 × 10-34 J s) × (3 × 1015 s-1) = 1.986 × 1018 J
(ii) Energy of photon (E) = hν = hc/λ, where λ= wavelength
h = 6.626 × 10-34 J s ; c = 3 × 108 m s-1 ; λ= 0.50 Å = 0.5 × 10-10 m. ∴ E = (6.626 × 10-34 J s) × (3 × 108 ms-1) / 0.5 × 10-10 m = 3.98 x 10-15 J.
Q 2.7. Calculate the wavelength, frequency, and wavenumber of lightwave whose period is 2.0 × 10^-10 s.
A 2.7 Wavelength, λ = c/v = (3 × 108 ms-1) / (5 × 109 s-1) = 6.0 x 10-2 m Frequency, ν = 1/period = 1 / 2.0 × 10-10 s = 5.0 x 109 s-1 Wavenumber, (ṽ) = = 1 /λ (6.0 x 10-2 m) = 16.66 m-1
Q 2.8. What is the number of photons of light with wavelength 4000 pm which provide 1 Joule of energy?
A 2.8 Given: h = 6.626 × 10-34 Js, c = 3 × 108 m s-1, λ = 4000 pm = 4000 × 10-12 m = 4 × 10-9 m Energy of photon (E) = hc / λ = (6.626 × 10-34 Js) x (3 × 108 m s-1) / (4 × 10-9 m) = 4.969 x 10-17 J i.e. 4.969 x 10-17 J is the energy of 1 photon Therefore, 1 J is the energy of photons = 1 / (4.969 x 10-17) = 2.012 x 1016 photons.
Q 2.9.A photon of wavelength 4 × 10^-7 m strikes on metal surface; the work function of the metal being 2.13 eV. Calculate (i) the energy of the photon, (ii) the kinetic energy of the emission (iii) the velocity of the photoelectron. (Given 1 eV = 1.6020 × 10^-19 J).
A 2.9 Energy of photon (E) = hc / λ = (6.626 × 10-34 Js) x (3 × 108 m s-1) / (4 × 10-7 m) = 4.969 x 10-19 J Since, 1.6020 × 10-19 J= 1 eV So, 1 J= (1 eV) / (1.6020 × 10-19 J) Hence, 4.969 x 10-19 J = (1eV) x (4.969 x 10-19 J) / (1.602 x 10-19 J) = 3.1 eV (ii) Kinetic energy of emission = Energy – work function = (3.1 – 2.13) = 0.97 eV (iii) Kinetic energy of emission = 0.97 eV => ½ mv2= 0.97 eV = 0.97 x 1.602 x 10-19 J = 0.97 x 1.602 x 10-19 kg m2 s-2 => v2 = (2 x 0.97 x 1.602 x 10-19 kg m2 s-2 ) / (9.1 x 10-31 kg) = 0.34 x 1012 m2 s-2 => v = (0.34 x 1012 m2 s-2)1/2 = 0.583 x 106 ms-1 = 5.83 x 105 ms-1
Q 2.10. Electromagnetic radiation of wavelength 242 nm is just sufficient to ionise the sodium atom. Calculate the ionisation energy of sodium in kJ mol^-1.
A 2.10 Given: λ = 242 nm = 142 x 10-9 m, c = 3 x 108 ms-1, h = 6.626 x 10-34Js We know, E = hc / λ = (6.626 × 10-34 Js) x (3 × 108 m s-1) / (242 × 10-9 m) = 0.0821 x 10-17 J ∴ Ionization energy per mol (E) = (0.0821 x 10-17 J) x (6.022 x 1023 mol-1J) / 1000 = 494 kJ mol-1.
Q 2.11. A 25 watt bulb emits monochromatic yellow light of wavelength 0.57 μm. Calculate the rate of emission of quanta per second.
A 2.11 Energy of one photon (E) = hc / λ = (6.626 × 10-34 Js) x (3 × 108 m s-1) / (0.57 × 10-6 m) = 3.48 x 10-19 J Rate of emission of quanta per second = Power / Energy = (25 watt) / (3.48 x 10-19 J) = (25 Js-1) / (3.48 x 10-19 J) = 7.18 x 1019 s-1.
Q 2.12. Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 Å. Calculate threshold frequency (v0) and work function (W0) of the metal.
A 2.12 Threshold frequency (v0) = c /λ = (3 × 108 m s-1) / (68 x 10-8 m) = 4.41 x 1014 s-1 Work function (W0) = hv0 =(6.626 × 10-34 Js) x (4.41 x 1014 s-1) = 2.92 x 10-19 J.
Q 2.13. What is the wavelength of the light emitted when the electron in a hydrogen atom undergoes transition from the energy level with n = 4 to energy level n = 2? What is the colour corresponding to this wavelength? (Given RH = 109678 cm-1)
A 2.13 According to Balmer formula, Wave number (ῡ) = RH[1/n12 - 1/n22 ]cm-1 = 109678[1/22 – 1/42] cm-1 = (109678 x 3) / 16 cm-1 λ = 1 / ῡ = 16 / (109678 x 3) cm = 16 x 107 / (109678 x 3) nm = 486 nm
Q 2.14. How much energy is required to ionise a hydrogen atom if an electron occupies n = 5 orbit? Compare your answer with the ionisation energy of H atom (energy required to remove the electron from n = 1 orbit)
A 2.14 Energy of a hydrogen present in a particular energy shell, En = 13.12 x 105 / n2 J mol-1 = (13.12 x 105) / (n2 x 6. 022 x 1023) J atom-1 = -2.18 x 10-18 / n2 J atom-1 Step I: Ionisation energy for hydrogen electron present in orbit n = 5 IE5 = E∞ - E5 = 0 – [(-2.18 x 10-18) / 25] J atom-1 = 8.72 x 10-20 J atom-1 Step II: Ionisation energy for hydrogen electron present in orbit n = 1 IE1 = E∞ - E1 = 0 – [(-2.18 x 10-18) / 1] J atom-1 = 2.18 x 10-18 J atom-1 Therefore IE1 / IE5 = (2.18 x 10-18 J atom-1) / (8.72 x 10-20 J atom-1) = 25 The energy required to remove an electron from first orbit in a hydrogen atom is 25 times the energy needed to remove the electrons from the fifth orbit.
Q 2.15. What is the maximum number of emission lines when the excited electron of a hydrogen atom in n = 6 drops to the ground state?
A 2.15 The maximum no. of emission lines = [n(n–1)] /2 = [6(6–1)] / 2 =3 × 5 = 15 The transitions that take place are as follows:
| n = 6 to n = 1 | n = 5 to n = 1 | n = 4 to n = 1 | n = 3 to n = 1 | n = 2 to n = 1 |
| 6 → 5 | 5 → 4 | 4 → 3 | 3 → 2 | 2 → 1 |
| 6 → 4 | 5 → 3 | 4 → 2 | 3 → 1 | |
| 6 → 3 | 5 → 2 | 4 → 1 | ||
| 6 → 2 | 5 → 1 | |||
| 6 → 1 | ||||
| 5 lines | 4 lines | 3 lines | 2 lines | 1 line |
Q 2.16. (i) The energy associated with first orbit in hydrogen atom is –2.17 × 10^-18 J atom^-1. What is the energy associated with the fifth orbit? (ii) Calculate the radius of Bohr’s fifth orbit for hydrogen atom.
A 2.16 (i) For an electron, the energies in the two orbits can be compared as: E1 / E2 = (n2 / n1)2 [Since E is inversely proportional to n2] Given: n1 = 1, E1 = –2.17 × 10-18 J atom-1, n2 = 5 Therefore, (–2.17 × 10-18 J atom-1) / E2 = (5 / 1) 2 = 25 => E2 = (–2.17 × 10-18 J atom-1) / 25 = –8.77 x 10-20 J atom-1
(ii) For hydrogen atom; rn = 0.529 x n2 Å
r5 = 0.529 x (5)2 = 13.225 Å = 1.3225 nm.
Q 2.17. Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
A 2.17 According to Balmer formula, ῡ = 1 / λ = RH [1/n12 – 1/n22] For the longest wavelength transition in the Balmer series of atomic hydrogen, wave number must be least. This is possible in case n2 – n1 = minimum; i.e. n1 = 2 and n2 = 3. Substituting the values: ῡ = 1 / λ = (1.097 x 107 m-1) [1/22 – 1/32] = (1.097 x 107 m-1) [5/36] = 1.523 x 106 m-1
Q 2.18. What is the energy in joules required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of light emitted when the electron returns to the ground state? The ground state electronic energy is – 2.18 × 11^-11 ergs.
A 2.18 Step I: calculation of energy required Energy of electron (En) = (- 2.18 x 10-11ergs) / n2= (- 2.18 x 10-18 J) / n2 Energy in Bohr’s 1st orbit (E1) = (- 2.18 x 10-18 J) / 12 Energy in Bohr’s 5th orbit (E1) = (- 2.18 x 10-18 J) / 52 Therefore, energy required (ΔE) = E5 – E1 = [(- 2.18 x 10-18 J) / 25] – [(- 2.18 x 10-18 J) / 1] = 2.18 x 10-18 (1 – 1/25) J = 2.18 x 10-18 x 24 / 25 = 2.09 x 10-18 J Step II: Calculation of wavelength of light emitted λ = hc / ΔE = (6.626 x 10-34 J s) x (3 x 108 ms-1) / (2.09 x 10-18 J) = 9.50 x 10-8 m = 950 A⸰.
Q 2.19. The electronic energy in hydrogen atom is given by En = -2.18 × 10^-18 / n^2J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
A 2.19 Step I: Calculation of energy required ΔE = E∞– E2 = 0 – (–2.18 × 10-18 J) / 4 = 5.45 x 10-19 J Step II: Calculation of the longest wavelength of light in cm used to cause the transition λ = hc / ΔE = (6.626 x 10-34 J s) x (3 x 108 ms-1) / (5.45 x 10-19 J) = 3.644 x 10-7 x 102 = 3.645 x 10-5 cm.
Q 2.20 Calculate the wavelength of an electron moving with a velocity of 2.05 × 10^7 m s^-1.
A 2.20 We know that the mass of an electron, me = 9.1 x 10-31 kg, Velocity of electron, v = 2.05 × 107 m s-1 We know that Planck’s constant, h = 6.626 x 10-34 kg m2 s-1 As per de Broglie’s equation, = (6.626 x 10-34 kg m2 s-1) / (9.1 x 10-31 kg) x (2.05 x 107 m s-1) = 3.55 x 10-11 m
Q 2.21 The mass of an electron is 9.1 × 10^-31 kg. If its kinetic energy is 3.0 × 10^-25 J, calculate its wavelength.
A 2.21 Kinetic energy. K.E. = ½ mv2 => v2 = (2 x K.E.) / m Given, K.E. = 3 x 10-25 J = 3 x 10-25 kg m2 s-2 Therefore,v2 = [2 x (3 x 10-25 kg m2 s-2)] / 9.1 x 10-31 kg => v2= 65.9 x 104 m2 s-2 =>v = 8.12 x 102 m s-1 To calculate the wavelength of the electron According to de Broglie’s equation, = (6.626 x 10-34 kg m2 s-1) / (9.1 x 10-31 kg) x (8.12 x 102 m s-1) = 0.08967 x 10-5 m = 8967 x 10-10 m = 8967Å
Q 2.22 Which of the following are iso-electronic species i.e., those having the same number of electrons? (Beginner) .
Na+, K+, Mg2+, Ca2+, S2-, Ar
A 2.22 Na+ and Mg2+ are iso-electronic species having 10 electrons each. K+, Ca2+, S2- are iso-electronic species having 18 electrons each.
Q 2.23.(i) Write the electronic configuration of the following ions : (a) H (b) Na+ (c) O^2- (d) F–. (ii) What are the atomic numbers of the elements whose outermost electronic configurations are represented by:
(a) 3s1 (b) 2p3 and (c) 3p5?
(iii) Which atoms are indicated by the following configurations?
(a) [He]2s1 (b) [Ne] 3s2 3p3 (c) [Ar] 4s2 3d1.
A 2.23 i) (a)1s2(b)1s2 2s2 2p6(c) 1s22s22p6(d) 1s22s22p6.
(ii) (a) Na (Z = 11) has outermost electronic configuration = 3s1
(b) N (Z = 7) has outermost electronic configuration = 2p3
(c) Cl (Z = 17) has outermost electronic configuration = 3p5
(iii) (a) Li(b) P(c) Sc
Q 2.24. What is the lowest value of n which allows ‘g’ orbital to exist?
| Value of l |
0 | 1 | 2 | 3 | 4 | 5 |
| Subshell notation | s | p | d | f | g | h |
| number of orbitals | 1 | 3 | 5 | 7 | 9 | 11 |
A 2.24 The lowest value of l where ‘g’ orbital can be present = 4 As for any value ‘n’ of principal quantum number, the Azimuthal quantum number (l) can have a value from zero to (n – 1). ∴ For l = 4, the minimum of n where ‘g’ orbital can be present = 4+1=5.
Q 2.25. An electron is in one of the 3d orbitals. Give the possible values of n, l and nil for the electron. (Beginner)
A 2.25 For electron in 3d orbital, n = 3, l = 2, mi = -2, -1, 0, +1, +2
Q 2.26. An atom of an element contains 29 electrons and 35 neutrons. Deduce (i) the number of protons and (ii) the electronic configuration of the element.
A 2,26 (i) No. of protons in a neutral atom = No. of electrons = 29
(ii) Electronic configuration = 1s2 2s2 2p6 3s2 3p6 3d10 4s1.
Q 2.27. Give the number of electrons in the species: H2+, H2 and O2+.
- A 2.27 Number of electrons in:
- (i) H2+ = 1
- (ii) H2 = 2
- (iii) O2+ = 15
Q 2.28. (i) An atomic orbital has n = 3. What are the possible values of l and ml ? (ii) List the quantum numbers ml and l of electron in 3rd orbital. (iii) Which of the following orbitals are possible? 1p, 2s, 2p and 3f.
A 2.28 (i) For n = 3; l = 0, 1 and 2.
For l = 0 ; ml = 0
For l = 1; ml = +1, 0, -1
For l = 2 ; ml = +2, +1,0, +1, + 2
(ii) For an electron in 3rd orbital ; n = 3; l = 2 ; ml can have any of the values -2, -1, 0,
+ 1, +2.
(iii) For 1p orbital, n and l are both equal to 1. Since, l should always have a lower value than n. So, 1p ortial does not exist. For 3f orbital, n=3 and l=3. For the same reason, the existence of 3f orbital is not possible. 1p and 3f orbitals are not possible.
Q 2.29.Using s, p and d notations, describe the orbitals with following quantum numbers: (a) n = 1, l = 0 (b) n = 4, l = 3 (c) n = 3, l = 1 (d) n = 4, l = 2
A 2.29 (a) 1s orbital
(b) 4f orbital
(c) 3p orbital
(d) 4d orbital
Q 2.30. From the following sets of quantum numbers, state which are possible. Explain why the others are not possible.
(a) n = 0, l = 0, ml = 0, ms = + ½
(b) n = 1, l = 0, ml = 0, ms = – ½
(c) n = 1, l = 1, ml = 0, ms = + ½
(d) n = 2, l = 1, ml = 0, ms = – ½
(e) n = 3, l = 3, ml = –3, ms = + ½
(f) n = 3, l = 1, ml = 0, ms = + ½
A 2.30 (a) The set of quantum numbers is not possible because the minimum value of n can be 1 and not zero.
(b) The set of quantum numbers is possible.
(c) The set of quantum numbers is not possible because, for n = 1, l cannot be equal to 1. It can have 0 value.
(d) The set of quantum numbers is possible.
(e) The set of quantum numbers is not possible because, for n = 3, l cannot be 3.
(f) The set of quantum numbers is possible.
Q 2.31. How many electrons in an atom may have the following quantum numbers? (a) n = 4; ms = -1/2 (b) n = 3, l = 0.
A 2.31 (a) For n = 4
Total number of electrons = 2n2 = 2 × 16 = 32
Half out of these will have ms = -1/2
∴ Total electrons with ms (-1/2) = 16
(b) For n = 3
l= 0; ml = 0, ms +1/2, -1/2 (two e–)
Q 2.32. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
A 2.32 According to Bohr’s theory, mvr = nh / 2π => 2πr = nh/mv => mv = nh / 2πr -------------------------- (i) According to de Broglie equation, h / λ ------------------------------ (ii)
Comparing equations (i) and (ii) nh / 2πr = h / λ => 2πr = n λ Thus, the circumference (2πr) of the Bohr orbit for hydrogen atom is an integral multiple of the de Broglie wavelength.
Q 2.33. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of He+ spectrum?
A 2.33 For an atom, ῡ = 1/ λ = RH Z2[(1/n12) – (1/n22)] For He+ spectrum: Z = 4, n2 = 4, n1 = 2. ∴ ῡ = 1/ λ = RH Z2[(1/22) – (1/42)] = RH 22[(1/22) – (1/42)] = 3RH /4 For hydrogen spectrum: ∴ ῡ = 1/ λ = RH 12[(1/n12) – (1/n22)] = 3RH /4 =>(1/n12) – (1/n22) = 3/4 This corresponds to n1 = 1 and n2 =2 and means that the transition has taken place in the Lyman series from n = 2 to n =1.
Q 2.34. Calculate the energy required for the process: He+ (g) → He2+ (g) + e– The ionisation energy for the H atom in the ground state is 2.18 × 10^-18 J atom-1
A 2.34 The expression for the ionization energy atom, En = (2.18 × 10-18 x Z2) / n2 J atom-1 For H atom, (Z = 1). So, En =2.18 × 10-18 × (l)2 J atom-1 (given) For He+ ion (Z = 2). So, En =2.18 × 10-18 × (2)2 = 8.72 × 10-18 J atom-1 (one electron species)
Q 2.35. If the diameter of carbon atom is 0.15 nm, calculate the number of carbon atoms which can be placed side by side in a straight line across a length of a scale of length 20 cm long.
A 2.35 Length of scale = 20 cm = 20 x 107 nm = 2 x 108 nm Diameter of carbon atom = 0.15 nm ∴ Number of carbon atoms which can be placed side by side in a straight line across a length of a scale of length 20 cm = (2 x 108 nm) / (0.15 nm) = 1.33 x 109
Q 2.36. 2 × 10^8 atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is 2.4 cm.
A 2.36 The length of the arrangement = 2.4 cm
Total number of carbon atoms present = 2 ×108 Diameter of each C-atom = (2.4 cm) / (2 x 108) = 1.2 x 10-8 cm Radius of each C-atom = ½ x 1.2 x 10-8 cm = 6.0 x 10-9 cm = 0.06 nm
Q 2.37. The diameter of zinc atom is 2.6 Å. Calculate (a) the radius of zinc atom in pm (b) number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side length wise.
A 2.37 (a) The diameter of zinc atom is 2.6 Å =2.6×10−10m. The radius of Zn atom is (2.6×10−10) / 2=1.3×10−10m=130×10−12m=130 pm. (b) The number of Zn atoms present on 1.6 cm of length are 1.6 / (2.6×10−8) =6.154×107.
Q 2.38. A certain particle carries 2.5 x 10^-16 C of static electric charge. Calculate the number of electrons present in it.
A 2.38 Static electric charge (q) = 2.5 x 10-16 C Charge on one electron (e) = 1.602 x 10-19 C No. of electrons present = (2.5 x 10-16 C) / (1.602 x 10-19 C) = 1560
Q 2.39. In Millikan’s experiment, the charge on the oil droplets was found to be -1.282 x 10^-18C. Calculate the number of electrons present in it.
A 2.39 Charge on oil droplet = – 1.282 x 10-18C Charge on an electron = – 1.602 x 10-19C Number of electrons = q /e = (– 1.282 x 10-18C) / (– 1.602 x 10-19C) = 8
Q 2.40. In Rutherford experiment, generally the thin foil of heavy atoms like gold, platinum etc. have been used to be bombarded by the α-particles. If a thin foil of light atoms like aluminium etc. is used, what difference would be observed from the above results?
A 2.40 Heavy metals have a heavy nucleus and contain a large amount of positive change in their nucleus. By using heavy metals like gold and platinum in Rutherford’s experiment, a large number of α-particles get deflected and experience a repulsion thus finding it hard for these α-particles to retrace their path. If a thin foil of lighter atoms like aluminium were used in the Rutherford’s experiment, the obstruction offered to the path of the fast moving α-particles would be comparatively quite less. As a result, the number of α-particles deflected will be quite less and the particles which are deflected back will be negligible.
Q 2.41. Find the question below
Symbols 3579Br and 79Br can be written, whereas symbols 7935Br and 35Br are not acceptable. Answer briefly.
A 2.41 The composition of any atom can be represented by using the normal element symbol (X) with super-script on the left hand side as the atomic mass number (A) and subscript (Z) on the left hand side as the atomic number (i.e., AZX). No two elements can have the same atomic number. However, the mass numbers have to be mentioned in order to identify the elements. Thus, symbols 7935Br and 79Br are accepted because atomic number of Br will remain 35 even if not mentioned. For a given element, the number of protons is the same for the isotopes, whereas the mass number can be different for the given atomic number. Hence, correct placement of atomic number and mass number for an element to represent as a symbol
Q 2.42. An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
A 2.42 An element can be identified by its atomic number only. Let us find the atomic number.
Let the number of protons = x
Number of neutrons = x + (x×31.7/100) = 1.371x
Now, Mass no. of element = no. of protons + no. neutrons ⇒ x + 1.317x = 81
⇒ x = 34.958 x ≃ 35 ∴ No. of protons = 35, No. of neutrons = 81 – 35 =46
Atomic number of element (Z) = No. of protons = 35
The element with atomic number (Z) 35 is bromine (3579Br)
Q 2.43. An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons, find the symbol of the ion.
A 2.43 Let the no. of electron in the ion = x
∴ The no. of protons = x – 1 (as the ion has one unit negative charge)
and the no. of neutrons = x + (x×11.1 / 100) = 1.111 x
Mass of the ion = No. of protons + No. of neutrons
(x – 1) + (1.111 x)
Given mass of the ion = 37
∴ (x – 1) + (1.111 x) = 37 => 2.111 x = 37 + 1 = 38
x = 38 / 2.111 = 18
No. of electrons = 18; No. of protons = 18 – 1 = 17
Atomic no. of the ion = 17; atom corresponding to ion = Cl
Symbol of the ion = 3717Cl–
Q 2.44. An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign symbol to the ion.
A 2.44 Let the no. of electrons in the ion= x
∴ the no. of the protons= x + 3 (as the ion has three units positive charge)
and the no. of neutrons= x + (x×30.4 / 100) = x+ 0.304 x
Now, mass no. of ion = No. of protons + No. of neutrons = (x + 3) + (x + 0.304x)
∴ 56 = (x + 3) + (x + 0.304x) =>2.304x = 56 – 3 = 53
=>x = 53 / 2.304 = 23
Atomic no. of the ion (or element) = 23 + 3 = 26
The element with atomic number 26 is iron (Fe) and the corresponding ion is Fe3+.
Q 2.45. Arrange the following type of radiations in increasing order of wavelength: (a) radiation from microwave oven (b) amber light from traffic signal (c) radiation from FM radio (d) cosmic rays from outer space and (e) X-rays
A 2.45 The given radiations in increasing order of wavelength are: Cosmic rays < X-rays < radiation from microwave oven < amber light from traffic signal < radiation from FM radio.
Q 2.46. Nitrogen laser produces radiation of wavelength of 337.1 nm. If the number of photons emitted is 5.6 x 10^24, calculate the power of this laser.
A 2.46 Power of the laser E = Nhv = Nh c/λ, where N is the number of photos emitted = [(5.6 x 1024) x (6.626 x 10-34Js) x (3 x 108 ms-1)] / (337.1 x 10-9 m) = 3.3 x 106 J
Q 2.47. Neon gas is generally used in sign boards. If it emits strongly at 616 nm, calculate: (a) frequency of emission (b) the distance travelled by this radiation in 30s (c) energy of quantum (d) number of quanta present if it produces 2 J of energy.
A 2.47 (a) Frequency of emission, ν = c/λ = (3.0 x 108 ms-1) / (616 x 10-9 m) = 4.87 x 1014 s-1 (b) Speed of radiation, c = 3 x 108 ms-1 Distance travelled by this radiation in 30s = 3 x 108 ms-1 x 30 s = 9.0 x 109 m (c) Energy of quantum, E = hν =hc/λ = [(6.626 x 10-34Js) x (3 x 108 ms-1)] / (616 x 10-9 m) = 32.27 x 10-20 J (d) Number of quanta present if it produces 2 J of energy = (Total energy) / (Energy per quanta) = 2J / (32.27 x 10-20 J) = 6.2 x 1018
Q 2.48 In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 x 10^-18 J from the radiations of 600 nm, calculate the number of photons received by the detector.
A 2.48 Energy of one photon, E = hν = 6.626 x 10-34Js) x (3 x 108 / 2 ms-1) / 600 x 10-9 = 3.31 x 10-19 J No. of photons = (3.15 x 10-18) / 3.31 x 10-19 = 9.52 ≈ 10.
Q 2.49 Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nano second range. If the radiation source has the duration of 2 ns and the number of photons emitted during the pulse source is 2.5 x 10^15, calculate the energy of the source.
A 2.49 Time duration, t = 2 ns = 2 x 10-9 s Frequency, ν = 1 / t = 1 / 2 x 10-9 s = 109 / 2 s-1 Energy of one photon, E = hν = 6.626 x 10-34Js) x (109 / 2 s-1) = 3.25 x 10-25 J No. of photons = 2.5 x 105 Energy of source = 3.3125 x 10-25 J x 2.5 x 1015 = 8.28 x 10-10 J
Q 2.50. The longest wavelength doublet absorption transition is observed at 589 nm and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
A 2.50 λ1 = 589 nm = 589 x 10-9 m ν1 = c / λ1 = (3 x 108 ms-1) / (589 x 10-9 m) = 5.0934 x 1014 s-1 λ2 = 589.6 nm = 589.6 x 10-9 m ν2 = c / λ2 = (3 x 108 ms-1) / (589.6 x 10-9 m) = 5.0882 x 1014 s-1 ΔE = E1 – E2 = h [ν1 – ν2] = (6.626 x 10-34Js) x [(5.0934 x 1014 s-1) – (5.0882 x 1014 s-1) = 3.31 x 10-22 J
Q 2.51. The work function for caesium atom is 1.9 eV. Calculate (a) the threshold wavelength and (b) the threshold frequency of the radiation. If the caesium element is irradiated with a wavelength 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.
A 2.51 W0 = 1.9 eV = 1.9 x 1.602 x 10-19 J Threshold frequency, v0 = W0 / h = (1.9 x 1.602 x 10-19 J) / (6.626 x 10-34Js) = 0.459 x 1015 s-1 = 4.59 x 1014 s-1 Threshold wavelength, λ0 = c / v0 = (3 x 108 ms-1) / (4.59 x 1014 s-1) = 0.6536 x 10-6 m = 653.6 nm ≈ 654 nm Kinetic energy, E = E0 + ½ mv2 (1/2 mv2) = E – E0 = hc [(1/ λ) – (1/λ0)] = (6.626 x 10-34Js) x (3 x 108 ms-1) / (10-9) x [(1/500) – (1/654)] = 6.626 x 3 x 154 x 10-34+8+9) / (500 x 654) = 9.36 x 10-20 J Velocity, v = [(2 x 9.36 x 10-20) / m]1/2 = [(2 x 9.36 x 10-20) kg m2 s-2 / 9.1 x 10-31 kg]1/2 = (2.057 x 1011 m2s-2)1/2= (20.57 x 1010 m2s-2)1/2 = 4.5356 x 105 ms-1
Q 2.52. Following results are observed when sodium metal is irradiated with different wavelengths. Calculate (a) threshold wavelength and, (b) Planck’s constant.
| λ (nm) | 500 | 450 | 400 |
| v × 10–5 (cm s–1) | 2.55 | 4.35 | 5.35 |
A 2.52
Let the threshold wavelength be λ0 nm or λ0 × 10−9 m. h(ν−ν0) = ½ mv2 hc(1/λ−1/λ0)= ½ mv2 hc[(1/500×10−9) – (1/ λ0×10−9)] = ½ m(2.55×106)2 .........................(1) Similarly, hc[(1/450×10−9) – (1/λ0×10−9)] = ½ m(4.35×106)2 .......................................(2) Similarly, hc[(1/400×10−9) – (1/λ0 × 10−9)] = ½ m(5.2 × 106)2 ....................................(3) Divide equation (2) by (1), [(λ0 – 450) /450λ0] x – [500λ0/(λ0 – 500)] = (4.35/ 2.55)2 (λ0 – 450)/ (λ0 – 500) = 2.61 λ0= 531 nm. This is the threshold wavelength. The value of the threshold wavelength is substituted in equation (3). h ×3×108(1/400×10−9– 1/531×10−9)= ½ ×9.11×10−31×(5.2×106)2 h=6.84×10−34Js
Q 2.53. The ejection of the photoelectrons from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for silver metal.
A 2.53 λ = 256.7 nm = 256.7 x 10-9 m K.E. = 0.35 eV E = hc/ λ = (6.626 x 10-34Js) / (3 x 108 ms-1) / (256.7 x 10-9 m) = (6.626 x 3 x 10-17) J/ 256.7 = (6.626 x 3 x 10-17) / (256.7 x 1.602 x 10-19) eV E = 4.83 eV The potential applied to silver gets converted into kinetic energy of the photoelectron. So, Kinetic energy, K.E= 0.35 V => K.E= 0.35 eV E = W0 + K.E. => W0 = E – K.E. = 4.83 eV – 0.35 eV = 4.48 eV.
Q 2.54.If the photon of the wavelength 150 pm strikes an atom, one of its inner bound electrons is ejected out with a velocity of 1.5 x 10^7 m s^-1. Calculate the energy with which it is bound to the nucleus.
A 2.54 λ = 150 pm, v = 1.5 x 107 m s-1 Kinetic energy, K.E. = ½ mv2 = ½ x 9.1 x 10-31 kg x (1.5 x 107 ms-1)2 = [(9.1 x 1.5 x 1.5) / 2] x 10-31 +14 = 10.2375 x 10-17 J = 1.02375 x 10-16 J K.E = hc/ λ = (6.626 x 10-34 kg m2 s-1) / (3 x 108 ms-1) / (1.5 x 10-10 m) = [(6.626 x 3) x 10-34+8+10] / 1.5 = 13.252 x 10-16 J We know, E = W0 + K.E. W0 = E – K.E. = (13.252 – 1.024) x 10-16 J = 12.228 x 10-16 J = 12.228 10-16 / 1.602 x 10-19 = 7.63 x 103 eV
Q 2.55. Emission transitions in the Paschen series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 x 10^15 (Hz) [1/3^2 – 1 /n^2]. Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
A 2.55 Given, ν = (3.29 x 1015 Hz) (1/32 – 1/n2) c/λ = (3.29 x 1015 Hz) (1/32 – 1/n2) (3 x 108 ms-1) / (1.285 x 10-6 m) = (3.29 x 1015 Hz) (1/32 – 1/n2) 2.3346 x 1014 = (3.29 x 1015 Hz) (1/32 – 1/n2) 2.3346 / 32.9 = 1/32 – 1/n2 0.071 = 1/9 – 1/n2 1/n2 = 1/9 – 0.071= 0.111 – 0.071 = 0.04 n2 = 1/ 0.04 = 25 => n = 5 For n = 5, Paschen series lies in infrared region of the spectrum.
Q 2.56.Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
A 2.56 Radius of orbit of H like species = (0.529 / Z) n2Å = (52.9 / Z) n2 pm r1 = 1.3225 nm = 1322.5 pm = (52.9 / Z) n12 r2 = 211.6 pm = 211.6 pm = (52.9 / Z) n22 ∴ r1 / r2 = 1322.5 / 211.6 =>n12 /n22 = 6.25 => n1/n2= (6.25)1/2 = 2.5 => n1 = 2.5 n2 => 10 n1= 25 n2 => 2 n1= 5 n2 If n1 = 2, then n2 = 5. That means transition occurs from 5th orbit to 2nd orbit. This means that the transition belongs to Balmer series. Now, wave number, ῡ = (1.097 x 107 m-1) x (1/22 – 1/52) = 1.097 x 107 x 21/100 m-1 = 23.037 x 105 m-1 λ = 1/ ῡ = 1/ 23.037 x 105 m-1 = 434 x 10-9 m = 434 nm This transition belongs to visible region of the spectrum of light
Q 2.57. Dual behaviour of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is 1.6 x 10^6 m s^-1, calculate de Brogile wavelength associated with this electron.
A 2.57 As per de Brogile’s equation, λ = h / mv = (6.626 x 10-34 kg m2 s-1) / (9.1 x 10-31 kg) x (1.6 x 106 ms-1) = 0.455 x 10-9 m = 0.455 nm = 455 pm.
Q 2.58. Similar to electron diffraction, neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
A 2.58 λ = 800 pm = 800 x 10-12 m m = 1.675 x 10-27 kg As per de Brogile’s equation, ν = h/mλ = (6.626 x 10-34 kg m2 s-1) / (1.675 x 10-27 kg) x (800 x 10-12 m), 6.626/1.675 X 8 x 10-34+27+10 = 0.494 x 103 ms-1 = 494 ms-1
Q 2.59. If the velocity of the electron in Bohr’s first orbit is 2.19 x 10^6 m s^-1, calculate the de Brogile wavelength associated with it.
A 2.59 ν = 2.19 x 106 m s-1 As per de Brogile’s equation, λ = h/mv = (6.626 x 10-34 kg m2 s-1) / (9.1 x 10-31 kg) x (2.19 x 106 m s-1) = 6.626/ 9.1 X 2.19 x 10-34+25 m = 0.33243 x 10-9 m = 332.43 pm
Q 2.60. The velocity associated with a proton moving in a potential difference of 1000 V is 4.37 x 10^5 m s^-1. If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
A 2.60 ν = 4.37 x 105 m s-1, m = 0.1 kg As per de Brogile’s equation, λ = h/mv = (6.626 x 10-34 kg m2 s-1) / (0.1 kg) x (4.37 x 105 m s-1) = 6.626/0.437 x 10-34-5 m = 1.516 x 10-38 m
Q 2.61. If the position of the electron is measured within an accuracy of ± 0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h/4π x 0.05 nm. Is there any problem in defining this value?
A 2.61 According to Heisenberg’s uncertainty principle, ∆x∆p = h/4π ∆p = h/4 π∆x Where, ∆x = uncertainty in the position of the electron ∆p = uncertainty in the momentum of the electron Given, ∆x = 0.002 nm = 2.0 x 10-12 m ∆p = h/4π∆x = (6.623 x 10-34 kg m2 s-1) / (4 x 3.142 x 2 x 10-12 m) = 2.638 x 10-23 kg m s-1 Hence, uncertainty in the momentum of the electron = 2.637 × 10–23 kg m s–1 Actual momentum = h/4π X 0.05nm = (6.623 x 10-34 kg m2 s-1) / (4 x 3.142 x 5 x 10-11 m) = 1.055 x 10-24 kg m s-1 Since actual momentum is smaller than the uncertainty in measuring momentum, therefore, the momentum of electron cannot be defined.
Q 2.62. The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. List if any of these combination(s) has/have the same energy
(i) n = 4, l = 2, ml = -2, ms = -1/2
(ii) n = 3, l = 2, ml = 1, ms = +1/2
(iii) n = 4, l = 1, ml = 0, ms = +1/2
(iv) n = 3, l = 2, ml = -2, ms = -111
(v) n = 3, l = l, ml = -1, ms = +1/2
(vi) n = 4, l = 1, ml = 0, ms = +1/2
A 2.62 The electrons may be assigned to the following orbitals :
(i) 4d
(ii) 3d
(iii) 4p
(iv) 3d
(v) 3p
(vi) 4p.
The increasing order of energy is :
(v) < (ii) = (iv) < (vi) = (iii) < (i)
Q 2.63. The bromine atom possesses 35 electrons. It contains 6 electrons in 2p orbital, 6 electrons in 3p orbital and 5 electrons in 4p orbital. Which of these electrons experiences lowest effective nuclear charge?
A 2.63 The nuclear charge experienced by electrons depends on the distance between the nucleus and orbital. The greater is this distance, the lesser is the effective nuclear charge. Among all the p orbitals, 4p orbital lies the farthest from the nucleus and thus experiences the lowest effective nuclear charge because of the maximum magnitude of screening or shielding effect.
Q 2.64.Among the following pairs of orbitals, which orbital will experience more effective nuclear charge (i) 2s and 3s (ii) 4d and 4f (iii) 3d and 3p?
A 2.64 Greater the penetration of the electron present in a particular orbital towards the nucleus more will be the magnitude of the effective nuclear charge. Based upon this
- 1. 2s orbital is closer to the nucleus than 3s orbital and hence it will experience more effective nuclear charge.
- 2. 4d orbital will experience more effective nuclear charge due to its closer proximity to 4f orbital.
- 3. 3p orbital will experience more effective nuclear charge as it is closer to the nucleus.
Q 2.65. The unpaired electrons in Al and Si are present in the 3p orbital. Which electrons will experience more effective nuclear charge from the nucleus?
A 2.65 Configuration of the two elements are: Al (Z = 13): [Ne]103s23p1; Si (Z = 14): [Ne]103s23p2
The unpaired electrons in silicon (Si) will experience more effective nuclear charge because the atomic number of the element Si is more than that of Al.
Q 2.66.Indicate the number of unpaired electrons in : (a) P (b) Si (c) Cr (d) Fe and (e) Kr.
A 2.66 (a) P (Z=15) : [Ne]103s23p3 ; No. of unpaired electrons = 3
(b) Si (Z=14) : [Ne]103s23p2 ; No. of unpaired electrons = 2
(c) Cr (Z=24): [Ar]184s13d5 ; No. of unpaired electrons = 6
(d) Fe (Z=26): [Ar]184s23d6 ; No. of unpaired electrons = 4
(e) Kr (Z=36) : [Ar]184s23d104p6 ; No. of unpaired electrons = Nil.
Q 2.67. (a) How many sub-shells are associated with n = 4? (b) How many electrons will be present in the sub-shells having ms value of -1/2 for n = 4? (Intermediate)
A 2.67. (a) For n = 4, No. of sub-shells = (l = 0, l = 1, l = 2, l = 3) = 4.
(b) Total number of orbitals which can be present = n2 = 42 = 16.
Each orbital can have an electron with ms = – 1/2. Total no. of electrons with m, = – 1/2 is 16.
News & Updates
Ncert Solutions Chemistry Class 11th Exam
Student Forum
Anything you would want to ask experts?Answered 4 days ago
Yes is there
N
Beginner-Level 2
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test
Jmi entrance test of 2023 for class 11th commerce?