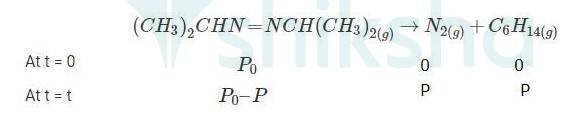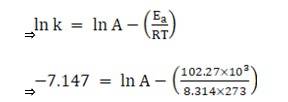NCERT Class 12 Chemistry Solution Chemical Kinetics: Chemical kinetics is the study of chemical reactions with respect to reaction rates, the effect of various variables, the rearrangement of atoms and the formation of intermediates. The rate of a reaction is concerned with a decrease in the concentration of reactants or an increase in the concentration of products per unit of time. It can be expressed as an instantaneous rate at a particular instant of time and an average rate over a large interval of time. A number of factors such as temperature, concentration of reactants, catalyst, affect the rate of a reaction.
Candidates can check here NCERT Class 12 Chemical Kinetics chapter solution to prepare for the exam effectively. These solutions of NCERT Chemistry Class 12 Chemical Kinetics have been prepared by subject experts. Chemical Kinetics NCERT Class 12 is an important chapter from which questions are asked in the board exam as well as JEE Mains/NEET.
NCERT Chemistry Class 12 Chemical Kinetics Topics
Candidates can check here the topics that are included in NCERT class 12 Chemistry Chemical Kinetics chapter.
- The rate of a Chemical Reaction
- Factors Influencing the Rate of a Reaction
- Dependence of Rate on Concentration
- Rate Expression and Rate Constant
- Order of a Reaction
- Molecularity of a Reaction
- Integrated Rate Equations
- Zero Order Reactions
- First-Order Reactions
- Half-Life of a Reaction
- Pseudo-First-Order Reaction
- Temperature Dependence of the Rate of a Reaction
- Effect of Catalyst
NCERT Chemistry Class 12th Solution PDF - Chemical Kinetics Chapter Download
The Chemical Kinetics chapter is an important chapter for the students because it forms a strong foundation for class XII students. It provides a glimpse of the scope of Chemistry to the students. The students can download here the Chemistry NCERT Class 12 PDF with solutions for free.
Download Here: NCERT Solution for Class XII Chemistry Chemical Kinetics PDF
Explore exams which ask questions on Chemistry Ncert Solutions Class 12th
Select your preferred stream
Chemical Kinetics Solutions and FAQs
Intext Q 4.1 For the reaction R → P, the concentration of a reactant changes from 0.03M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
A 4.1 Given-
Initial concentration (R1) = 0.03M
Final concentration (R2) = 0.02M
Time = 25 mins.
The formula for average rate of the reaction is,
rav = - Δ{R} / Δt → Equation 1
∵ {R} = (R2)-( R1), the equation 1 is written as,
rav = - R2 - R1 / Δt
= -0.02-0.03 / 25
= 4 X 10-4 mol L-1 min-1
The average rate of reaction in seconds is given by,
= 4 X 10-4 mol L-1 / 60 S
(dividing by 60 to convert minutes to seconds)
= 6.6 × 10-6 mol L-1 s-1
The average rate of the reaction in minutes is 4 × 10-4 mol L-1 min-1 and in seconds is 6.6 × 10-6 mol L-1 s-1
Intext Q 4.2 In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L–1 to 0.4 mol L–1 in 10 minutes. Calculate the rate during this interval?
A 4.2 Given-
Initial concentration (A1) = 0.5M
Final concentration (A2) = 0.4M
Time = 10 mins.
The formula for average rate of the reaction is,
rav = -1/2 X Δ{A} / Δt → Equation 1
∵ {A} = (A2)-( A1), the equation 1 is written as,
rav = -1/2 X A2 - A1 / Δt
= -1/2 X 0.4-0.5 / 10
= -1/2 X 0.1 / 10
= 0.005 mol L-1 min-1
= 5 × 10-3 mol L-1 min-1
The average rate of the reaction is 5 × 10-3 mol L-1 min-1
Intext Q 4.3 For a reaction, A + B → Product; the rate law is given by, r = k [ A]1/2 [B]2 . What is the order of the reaction?
A 4.3 The order of the reaction is sum of the powers of concentration of reactants in the rate law. According to this,
The order of the reaction = 1/2 + 2
= 2 1/2 or 2.5
The order of the reaction is 2.5
Intext Q 4.4 The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y?
A 4.4 Let the reaction be X→Y
As, this reaction follows second order kinetics, the rate of the reaction will be,
Rate = k(X)2 → Equation 1
Since the concentration of X is increased three times, Equation 1 will become,
Rate = k(3X)2
= k × 9(X)2
∴ The rate of formation of Y will become 9 times.
Thus, the rate of formation of Y will become 9 times
Intext Q 4.5 A first order reaction has a rate constant 1.15 × 10-3 s-1. How long will 5 g of this reactant take to reduce to 3 g?
A 4.5 Given-
Rate constant, k = 1.15 × 10-3 s-1
innitial quantity R0 = 5g
Final quantity, R = 3 g
According to the formula of first order reaction
K = 2.303/ t log R0 / R
1.15 X 10-3 = 2.303 /t log 5/3
t = 2.303 / 1.15 X 10-3 log 5/3
t = 443.8 s
t = 4.438 × 102 s
The time taken for 5g of the reactant to reduce to 3 g is 4.438 × 102 s
Intext Q 4.6 Time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
A 4.6 Given-
t1/2 = 60 mins
Using the formula for half life, t1/2 = 0.693/k , we get,
k= 0.693 / t1/2
k= 0.693 / 60
∴k = 1.155 × 10-2 min-1
The rate constant of the reaction, k is 1.155 × 10-2 min-1
Intext Q 4.7 What will be the effect of temperature on rate constant?
A 4.7 The rate constant of a chemical reaction normally increases with increase in temperature. It is observed that for a chemical reaction with rise in temperature by 10°C, the rate constant is nearly doubled and this temperature dependence of the rate of a chemical reaction can
be accurately explained by Arrhenius equation,
k = A
Thus, the rate constant of a chemical reaction normally increases with increase in temperature.
Intext Q 4.8 The rate of the chemical reaction doubles for an increase of 10K in absolute temperature from 298K. Calculate Ea .
A 4.8 Given-
Initial temperature, T1 = 298 K
Final temperature, T2 = 298 K + 10 K = 308 K
Knowing that the rate constant of a chemical reaction normally increases with increase in temperature, we assume that,
Initial value of rate constant, k1 = k
Final value of rate constant, k2 = 2k
Using Arrhenius equation,
Intext Q 4.9 The activation energy for the reaction 2 HI(g) → H2 + I2 (g) is 209.5 kJ mol–1 at 581K.Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
A 4.9 Given-
Energy of activation, Ea= 209.5 kJ mol–1
Ea in joules = 209.5 × 1000 = 209500 J mol–1
Temperature, T = 581K
Gas constant, R = 8.314 J K-1 mol-1
Using Arrhenius equation,
k = Ae-Ea/RT
In this equation, the term e-Ea/RT represents the number of molecules which have kinetic energy greater than the activation energy, Ea.
∴The number of molecules = e-Ea/RT → Equation 1 Substituting all the known values in equation 1, we get,
= e-209500/8.314X581
=e-43.3708
Finding the value of anti ln(43.3708), we get, 1.47 × 10-19
The fraction of molecules of reactants having energy equal to or greater than activation energy is 1.47 × 10-19
Exercise Q 4.1 From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3NO(g) → N2O (g) Rate = k[NO]2 (ii) H2O2 (aq) + 3I– (aq) + 2H+ → 2H2O (l) + 3 I − Rate = k[H2O2 ][I- ] (iii) CH3CHO (g) → CH4 (g) + CO(g) Rate = k [CH3CHO]3/2 (iv) C2H5Cl (g) → C2H4 (g) + HCl (g) Rate = k [C2H5Cl]
A 4.1
(i) 3NO(g) → N2O(g)
Rate = k[NO]2
Here rate law is dependent on concentration of NO only.And power raised to concentration of NO is 2. Hence order of reaction is 2.
To find dimensions of rate constant (K)- We know rate of chemical reaction is measured in (concentration / time). So, unit of K will be
(concentration) / (time) (concentration)2
i.e. [concentration]-1[ time]-1 . If concentration is in mol L-1 and time is in sec. then dimensions of k will be : mol-1 L sec-1
(ii) H2O2(aq) + 3I-(aq) + 2H+ → 2 H2O(l) + I3-
Rate = k[H2O2][I-]
Here rate law is dependent on concentration of H2O2 and I-. And power raised to concentration of H2O2 is 1, and power raised to concentration of I- is 1. order is sum of powers hence, order of given reaction is 2.
To find dimensions of rate constant (K)- We know rate of chemical reaction is measured in [concentration/time]. So, unit of K will be [Concentration]/[time][concentration]2 i.e. [concentration]-1[ time]-1. If concentration is in mol L-1 and time is in sec then dimensions of k will be mol-1 L sec-1
- (iii) CH3CHO(g) → CH4(g) + CO(g)
- Rate = k[CH3CHO]3/2
Here rate law is dependent on concentration of CH3CHO.And power raised to CH3CHO is 3/2. Hence order of reaction is 3/2.
To find dimensions of rate constant (K)- We know rate of chemical reaction is measured in [concentration/time]. So, unit of K will be [Concentration]/[time][concentration]3/2 i.e. [concentration]-
1/2[time]-1.
If concentration is in mol L-1 and time is in sec. Then dimensions of K will be mol-1/2L1/2 sec-1
- (iv) C2H5Cl (g) → C2H4(g) + HCl(g)
- Rate = k[C2H5Cl]
Here rate law is dependent on concentration of C2H5Cl. And power raised to C2H5Cl is 1. Hence order of reaction is 1.
To find dimensions of rate constant (K)- We know rate of chemical reaction is measured in [concentration/time]. So, unit of K will be [Concentration]/[time][concentration]1. i.e. [time]-1
If concentration is in mol L-1 and time is in sec. Then dimensions of K will be sec-1.
Exercise Q 4.2 For the reaction given below with k = 2.0 × 10–6 mol–2 L2 s–1. Calculate the initial rate of the reaction when [A] = 0.1 mol L^–1, [B] = 0.2 mol L^–1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L^–1.
2A + B → A2B the rate = k[A][B]2
A 4.2 a) Rate = k[A][B]2, Rate = 0 × 10-6[0.1][0.2]2
Rate = 8 × 10-9 mol L-1sec-1
b) 2A +B = A2B
=0.06+ 0.18 = 0.02
Situation when A is remained 0.06 mol L-1
Now, According to rate law, Rate = k[A][B]2
Rate = 2 × 10-6[0.06][0.18]2
i.e. Rate = 3.888 × 10-9 mol L-1sec-1
Initial rate of reaction is 8 × 10-9 mol L-1sec-1. and rate when concentration of A is 0.06 mol L-1 is 3.888 × 10-9 mol L-1sec-1.
Exercise Q 4.3 The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10^–4 mol^–1 L s^–1?
A 4.3
2NH3(g) → N2(g) + 3H2(g)
Rate of zero order reaction is equal to rate constant. i.e. Rate = 2.5 × 10-4mol L-1sec-1.
According to rate law,
-d[NH3] / 2dt = d[N2] / dt
2.5 × 10-4mol L-1sec-1 = d[N2] / dt
i.e. the rate of production of N2 is 2.5 × 10-4mol L-1 sec-1.
According to rate law,
-d[NH3] / 2dt = d[H2] / 3dt
d[H2] / dt = -3 X d[NH3] / 2dt
i.e. rate of formation of H2 is 3 times rate of reaction = 3 × 2.5 × 10-4mol L-1sec-1
= 7.5 × 10-4mol L-1sec-1
Rate of formation of N2 and H2 is 2.5 × 10-4 mol L-1sec-1 and 7.5 × 10-4 mol L-1sec-1 respectively
Exercise Q 4.4 The decomposition of dimethyl ether leads to the formation of CH4 , H2 and CO and the reaction rate is given by Rate = k [CH3OCH3 ] 3/2 The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., Rate= k(PCH3OCH3)^3/2 If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
A 4.4 Rate of given chemical reaction will be represented as
-d[pCH3OCH3] / dt
Hence units of rate is bar min-1
To find units of K, K = rate/[pCH3OCH3]3/2
The unit of k = bar -1/2min-1.
Units of Rate- bar min-1. and Units of Rate constant K : bar -1/2min -1
Exercise Q 4.5 Mention the factors that affect the rate of a chemical reaction.
A 4.5 Factors affecting rate of reaction-
- Temperature (increasing temperature increases rate of reaction)
- Concentration or pressure of reactants. (Increasing concentration or pressure increases rate of reaction)
- Presence or absence of a (Adding catalyst mostly increases the rate of reaction)
- The surface area of solid (If reaction is processing over solid reactant then increasing its surface area increases rate of reaction)
- Nature of reactants
Exercise Q 4.6 A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is (i) doubled (ii) reduced to half?
A 4.6 Let suppose reaction
A ⇒B; having rate law, Rate = K [A]2
- (i) If the concentration of A is doubled then the rate will affect by the square of concentration i.e. rate will become 22 = 4 times.
- (ii) If the concentration of A is halved then the rate will affect the square of concentration i.e (1/2)2 = 1/4
- (iii) Rate becomes 4 times of initial Rate (ii) Rate becomes 1/4 times of initial Rate
Exercise Q 4.7 What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?
A 4.7 Increase in temperature increases the rate constant of a reaction. as we know increase in temperature increases the rate of reaction to satisfy the equation Rate = k [concentration]n where n can be any real number. k have to increase as concentration is almost not changing over small temperature change.
Increasing temperature by 100C almost double the rate constant. This can be represented quantitively by the help of arrehinus equation-
K = Ae-Ea/RT, where k is rate constant, Ea is activation energy, R is universal gas constant, T is absolute temperature.
Exercise Q 4.8 In a pseudo first order hydrolysis of ester in water, the following results were obtained, Calculate the average rate of reaction between the time intervals 30 to 60 seconds.
| t/s |
0 |
30 |
60 |
90 |
| [Ester]/mol L-1 |
0.55 |
0.31 |
0.17 |
0.085 |
A 4.8 (i) Average rate of reaction over interval is [change in concentration]/[time taken] e.
[0.31 - 0.17] / [60-30] = 0.00467 mol L-1 sec-1
- (ii) the pseudo first-order rate constant can be calculated by K = (2.303/t) log(Ci/Ct)
- where K is Rate constant,
- t is time taken,
- Ci is initial concentration
- Ct is Concentration at time t.
- K = (2.303/30) log (0.55/0.31)
⇒K = 1.9 × 10-2 sec-1
- (i)Average rate between 30 to 60 sec is 0.00467 mol L-1sec-1
- (ii) Pseudo first order rate constant is 1.× 10-2sec-1
Exercise Q 4.9 A reaction is first order in A and second order in B. (i) Write the differential rate equation. (ii) How is the rate affected on increasing the concentration of B three times? (iii) How is the rate affected when the concentrations of both A and B are doubled?
A 4.9 Order is power raised to reactant in rate law, hence,
Rate = k[A][B]2
- (ii) When the concentration of B is increased three times then the rate is affected by the square of The rate is increased by 9 Times.
- (iii) When concentration of reactant both A and B is doubled then the rate will have affected as square of reactant B and Two times of Reactant Overall increase in rate is 8 times
- (a) When the concentration of B is increased by three times, the rate is increased by nine
- (b) When of both reactants doubled then Rate increased 8 times.
Exercise Q 4.10 In a reaction between A and B, the initial rate of reaction(r0)was measured for different initial concentrations of A and B are given below: What is the order of the reaction with respect to A and B?
| A/mol L-1 |
0.20 |
0.20 |
0.40 |
| B/mol L-1 |
0.30 |
0.10 |
0.05 |
| r0/mol L-1s-1 |
5.07 × 10-5 |
5.07 × 10-5 |
1.43 × 10-4 |
A 4.10 When concentration of B is changed then rate of reaction doesn't change that means order with respect to B is 0. But when the concentration of A is doubled rate increased by 2.82 times i.e.21.5 = 2.82.Hence order with respect to A is 1.5.
Order with respect to A and B is 1.5 and 0 respectively.
Exercise Q 4.11 The following results have been obtained during the kinetic studies of the reaction: 2A + B → C +D. Determine the rate law and the rate constant for the reaction.
| Experiment |
[A]/mol L-1 |
[B]/mol L-1 |
Initial rate of formation of D/mol L-1min-1 |
| I |
0.1 |
0.1 |
6.0 × 10-3 |
| II |
0.3 |
0.2 |
7.2 × 10-2 |
| III |
0.3 |
0.4 |
2.88 × 10-1 |
| IV |
0.4 |
0.1 |
2.40 × 10-2 |
A 4.11
By comparing Experiment I and IV if we increase the concentration of A by 4 times then Rate also increased by 4 times. That means order with respect to A is 1.
By comparing Experiment II and III if we double the concentration of B Rate increases by 4 times that means order with respect to B is 2.
Rate law of reaction will be, Rate = k [A][B]2
To find K, K = rate/[A][B]2 i.e. K = 6.0 × 10-3/[0.1][0.1]2
K = 6 mol-2L2sec-1
Order with respect to A and B is 1 and 2 respectively. And value of K(rate constant) is = 6 mol-2L2sec-1
Exercise Q 4.12 The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
| Experiment |
[A]/mol L-1 |
[B]/mol L-1 |
Initial rate/mol L-1 min-1 |
| I |
0.1 |
0.1 |
2.0 × 10-2 |
| II |
- |
0.2 |
4.0 × 10-2 |
| III |
0.4 |
0.4 |
- |
| IV |
- |
0.2 |
2.0 × 10-2 |
A 4.12 As reaction is first order with respect to A and zero Order with respect to B. Then changing the concentration of B won’t affect the rate of reaction and increasing concentration of A ‘n’ times will increase the rate by ‘n’ times. By this logic lets fill the table- In first blank space concentration of A will be 0.2 mol L-1 because the rate is doubled. In second blank space, Rate will be 8 × 10-2mol L-1min-
1 because the concentration of A is increased 4 Times. In third blank space concentration of A will be 0.1 mol L-1 because the rate is same as in experiment I.
| Experiment |
[A]/mol L-1 |
[B]/mol L-1 |
Initial rate/mol L-1 min-1 |
| I |
0.1 |
0.1 |
2.0 × 10-2 |
| II |
0.2 |
0.2 |
4.0 × 10-2 |
| III |
0.4 |
0.4 |
8.0 × 10-2 |
| IV |
0.1 |
0.2 |
2.0 × 10-2 |
Exercise Q 4.13 Calculate the half-life of a first order reaction from their rate constants given below: (i) 200 s^–1 (ii) 2 min^–1 (iii) 4 years^–1
A 4.13 Half life of first order reaction is, t1/2 = ln2/K where t1/2 is half life of first order reaction, K is rate constant of First order reaction.
(i) t1/2 = ln2/200 s-1
⇒t1/2 = 0.693/200 s-1 (∵ln2 = 0.693)
⇒t1/2 = 0.003465 sec.
- (ii) t1/2 = ln2/2 min-1
⇒t1/2 = 0.693/2 min-1 (∵ln2 = 0.693)
⇒t1/2 = 0.3465 min
- (iii) t1/2 = ln2/4 year-1
⇒t1/2 = 0.693/4 years -1 (∵ln2 = 0.693)
⇒t1/2 = 0.17325 year.
Half life of 3 reactions are 0.003465 sec, 0.3465 min, 0.17325 year respectively.
Exercise Q 4.14 The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.
A 4.14 Radio active decay occurs via first order rate law,
t1/2 = 5730 years. rate constant(k) of given decay is 0.693/t1/2
⇒0.693/5730 = 1.2 × 10-4 year-1
By first order integrated rate law age of sample will be,
T = ( 2.303 / 1.2 X 10-4 ) log (A0/At)
where T is the age of sample A0 is the initial activity of the sample. and At is the activity of sample at any time t
T = ( 2.303 / 1.2 X 10-4 ) log (A0/0.8 A0)
T = 0.18 × 104 years.
Age of given sample is 0.18 × 104 years.
Exercise Q 4.15 The experimental data for decomposition of N2O5 [2N2O5 → 4NO2 + O2 ] in gas phase at 318K are given below: (i)Plot [N2O5 ] against t. (ii) Find the half-life period for the reaction. (iii) Draw a graph between log[N2O5 ] and t. (iv) What is the rate law ? (v) Calculate the rate constant. (vi) Calculate the half-life period from k and compare it with (ii).
| t/s |
0 |
400 |
800 |
1200 |
1600 |
2000 |
2400 |
2800 |
3200 |
| 102 × [N2O5]/mol L-1 |
1.63 |
1.36 |
1.14 |
0.93 |
0.78 |
0.64 |
0.53 |
0.43 |
0.35 |
A 4.15
- (iv) As log [N2O5] vs time is straight line given reaction is first Hence its rate law will be, Rate = k[N2O5]
- (v) The slope of above graph is slope = 0.000209 K = 303 × slope
⇒4.82 × 10-4sec-1
Now, t1/2 = 0.693/K.
⇒0.693/4.82 × 10-4
⇒t1/2 = 1438 sec. which is almost equal to (ii)
Exercise Q 4.16 The rate constant for a first order reaction is 60 s^–1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
A 4.16 Given:
Order of the reaction = 1
Let, Initial concentration [R]°= x
Final concentration [R] = x/16
Rate constant k = 60 s-1
We know, time
t= 2.303 / k log R0 / R
t = 2.303 / 60 log (x/x/16)
t = 2.303 / 60s-1 log (1/1/16)
t = 2.303 X log 16 / 60s-1
Solving, we get t = 4.6 × 10-2s
Exercise Q 4.17 During nuclear explosion, one of the products is 90 Sr with half-life of 28.1 years. If 1µg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically?
A 4.17 Initial concentration, [R]° = 1μg
Final concentration, [R] Half-life t1/2 = 28.1 yrs Solution:
We know, t1/2 = 0.693/k Where, k – rate constant
⇒k = 0.693/ t1/2
⇒k = 0.693/(28.1 yrs)
⇒k = 0.0246 yrs-1
Also, t = 2.303 / k log R0 / R
If t = 10yrs, then, using the formula, we get,
t = 2.303 / k log R0 / R
10 = 2.303 / 0.0246 log 1 / R10
log 1 / R10 = 0.0246 X 10 / 2.303
log 1 / R10 = 0.246 / 2.303
1 / R10 = antilog (0.246 / 2.303)
1 / R10 = 1.278
⇒ R10 = 0.7824μg
If t = 60yrs, then again, we get,
60 = 2.303 / 0.0246 log 1 / R60
log 1 / R60 = 0.0246 X 60 / 2.303
log 1 / R60 = antilog (1.476 / 2.303)
1 / R60 = 4.374
⇒[R]60 = 0.228 μg
∴0.2278μg of 90Sr will be left after 60 years.
Exercise Q 4.18 For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
A 4.18 Let, initial concentration be [R]°
Concentration at 90% completion be ((100-90)/100)×[R]°
∴Concentration at 90% be 0.1[R]°
Concentration at 99% completion be ((100-99)/100)× [R]°∴Concentration at 99% be 0.01[R]°
we know time, t= 2.303/K log R0 / R
Time taken for 90% completion is
T90 = 2.303 / K log R0 / 0.1 R0
T90 = 2.303 / K log 1 / 0.1
T90 = 2.303 / K log 10 / 1
T90 = 2.303 / K
Time taken for 99% completion is
T99 = 2.303 / K log R0 / 0.01 R0
T99 = 2.303 / K log 1 / 0.01
T99 = 2.303 / K log 100 / 1
T99 = 2 X 2.303 / K
T99 = 2 T90
Hence, the time taken to complete 9% of the first order reaction is twice the time required for the completion of 90% of the reaction.
Exercise Q 4.19 A first order reaction takes 40 min for 30% decomposition. Calculate t1/2.
A 4.19 Given:
Time t = 40 min
When 30% decomposition is undergone, 70% is the concentration.
We know, time taken
t= 2.303/K log R0 / R
Where, k- rate constant
[R]0 - initial concentration
[R] - concentration at time 't'
40 = 2.303/K log R0 / 0.7 R0
40 = 2.303/K log 1 / 0.7
40 / 0.1549 = 2.303 / k
⇒258.23 = (2.303/k)
We know, Half-life t1/2 = 0.693/k
Which can be written as, t1/2 = 0.3010 × (2.303/k)
⇒t1/2 = 0.3010 × 258.23
⇒t1/2 = 77.72 min
Exercise Q 4.20 For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained. Calculate the rate constant.
|
t (sec) |
P(mm of Hg) |
|
0 |
35.0 |
|
360 |
54.0 |
|
720 |
63.0 |
A 4.20 When t = 0, the total partial pressure is P0 = 35.0 mm of Hg
When time t = t, the total partial pressure is Pt = P0 + p
P0-p = Pt-2p, but by the above equation, we know p = Pt-P0 Hence, P0-p = Pt-2( Pt-P0)
Thus, P0-p = 2P0 – Pt
We know that time
t= 2.303/K log R0 / R
Where, k- rate constant
[R]° -Initial concentration of reactant
[R]-Concentration of reactant at time ‘t’
Here concentration can be replaced by the corresponding partial pressures.
Hence, the equation becomes,
t= 2.303/K log P0 / P0 - P
t= 2.303/K log P0 / 2P0 - Pt
→ equation 1
At time t = 360 s, Pt = 54 mm of Hg and P0 = 30 mm of Hg, Substituting in equation 1,
360 = 2.303/k log 30 / (2X30)-54
k= 2.175 X 10-3 s-1
At time t = 720 s, Pt = 63 mm of Hg and P0 = 30 mm of Hg, Substituting in equation 1,
720 = 2.303 / k log 30 / (2X30) - 63
Thus, k = 2.235 × 10-3 s–1
Taking average, k = (2.235 × 10-3 s–1 + 2.175 × 10-3 s–1)/2
∴k = 2.21 × 10-3 s–1.
Exercise Q 4.21 Thte following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume. Calculate the rate of the reaction when total pressure is 0.65 atm.
SO2Cl2(g)→ SO2(g) + Cl2(g)
| Experiment |
Time/s–1 |
Total pressure/atm |
| 1 |
0 |
0.5 |
| 2 |
100 |
0.6 |
A 4.21 When t = 0, the total partial pressure is P0 = 0.5 atm
When time t = t, the total partial pressure is Pt = P0 + p
P0-p = Pt-2p, but by the above equation, we know p = Pt-P0
Hence, P0-p = Pt-2(Pt-P0)
Thus, P0-p = 2P0 – Pt
We know that time
t= 2.303/K log R0 / R
Where, k- rate constant
[R]° -Initial concentration of reactant [R]-Concentration of reactant at time ‘t’
Here concentration can be replaced by the corresponding partial pressures.
Hence, the equation becomes,
t= 2.303/K log P0 / P0 - P
t= 2.303/K log P0 / 2P0 - Pt
→ equation 1
At time t = 100 s, Pt = 0.6 atm and P0 = 0.5 atm,
Substituting in equation 1,
100 = 2.303/k log 0.5 / (2X0.5) - 0.6
Thus, k = 2.231 × 10-3 s-1
The rate of reaction R = k × PS02Cl2
When total pressure Pt = 0.65 atm and P0 = 0.5 atm, then
[PS02Cl2 = 2P0-Pt
Thus, substituting the values, PS02Cl2 = 2(0.5)-0.6 = 0.35 atm
R = k × PS02Cl2 = 2.231 × 10-3 s–1 × 0.35
Rate of the reaction R = 7.8 × 10-4atm s–1
Exercise Q 4.22 The rate constant for the decomposition of N2O5 at various temperatures is given below: Draw a graph between ln k and 1/T and calculate the values of A and Ea . Predict the rate constant at 30° and 50°C.
|
T/°C |
0 |
20 |
40 |
60 |
80 |
|
105 × k/s-1 |
0.0787 |
1.70 |
25.7 |
178 |
2140 |
A 4.22 To convert the temperature in °C to °K we add 273 K.
The graph is given as:
The Arrhenius equation is given by k = Ae-Ea/RT
Where, k- Rate constant
A- Constant
Ea-Activation Energy
R- Gas constant
T-Temperature
Taking natural log on both sides,
ln k = ln A-(Ea/RT)...................... equation 1
By plotting a graph, ln K Vs 1/T, we get y-intercept as ln A and Slope is –Ea/R.
Slope = (y2-y1)/(x2-x1)
By substituting the values, slope = -12.301
⇒–Ea/R = -12.301
But, R = 8.314 JK-1mol-1
⇒ aE= 8.314 JK-1mol-1 × 12.301 K
⇒ aE= 102.27 kJ mol-1
Substituting the values in equation 1 for data at T = 273K
(∵ At T = 273K, ln k =-7.147)
On solving, we get ln A = 37.911
∴ A = 2.91×106
When T = 300C, hence T = 30 + 273 = 303K
⇒ ln k =-2.8
⇒ k = 6.08x10-2s-1.
When T = 500C, hence T = 50 + 273 = 323K
Substituting in equation 1,
A = 2.91 × 106, Ea = 102.27 kJ mol-1
Ln K = ln(2.91 × 106)- 102.27/(8.314 × 323)
Thus, ln k = -0.5 and k = 0.607s-1.
Exercise Q 4.23 The rate constant for the decomposition of hydrocarbons is 2.418 × 10–5s – 1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor?
A 4.23
Given,
k = 2.418 × 10-5 s-1 T = 546 K
Ea = 179.9 kJ mol-1 = 179.9 × 103J mol-1
The Arrhenius equation is given by k = Ae-Ea/RT Taking natural log on both sides,
Ln k = ln A-(Ea/RT) Substituting the values,
ln(2.418 × 10-5 ) = ln A-179.9/(8.314 × 546) ln A = 12.5917
A = 3.9 × 1012 s-1(approximately)
Exercise Q 4.24 Consider a certain reaction A → Products with k = 2.0 × 10 –2s –1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L–1
A Given,
k = 2.0 × 10–2s-1
time t = 100s
Concentration [A0] = 1.0 mol L-1
We know,
On substituting the values, Log(1/[A]) = 2.303/2
Log[A] = -2.303/2 [A] = 0.135 mol L–1
Exercise Q 4.25 Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t 1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
A
t1/2 = 3.00 hours
We know, t1/2 = 0.693/k
∴k = 0.693/3 k = 0.231 hrs-1
We know, time Where, k- rate constant
[R]° -Initial concentration [R]-Concentration at time ‘t’
Thus, substituting the values, log([R]0/[R]) = 0.8
log([R]/[R]0) = -0.8
[R]/[R]0 = 0.158
Hence, 0.158 fraction of sucrose remains.
Exercise Q 4.26 The decomposition of hydrocarbon follows the equation
- k = (4.5 × 1011s–1) e-28000K/T. Calculate Ea
A 4.26
The given equation is
k = (4.5 x 1011 s-1) e-28000K/T (i)
|
Comparing, Arrhenius equation k = Ae -E/RT (ii)
We get, Ea / RT = 28000K / T
⇒Ea = R x 28000K
= 8.314 J K-1mol-1 × 28000 K
= 232792 J mol–1 or 232.792 kJ mol–1
Exercise Q 4.27 The rate constant for the first order decomposition of H2O2 is given by the following equation: log k = 14.34 – 1.25 × 104K/T. Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
A
We know, The Arrhenius equation is given by k = Ae-Ea/RT Taking natural log on both sides,
Ln k = ln A-(Ea/RT)
Thus, log k = log A -(Ea/2.303RT)......................................... eqn 1
The given equation is log k = 14.34 – 1.25 × 104K/T.............. eqn 2
Comparing 2 equations, Ea/2.303R = 1.25 × 104K
Ea = 1.25 × 104K × 2.303 × 8.314
Ea = 239339.3 J mol-1 (approximately) Ea = 239.34 kJ mol-1
Also, when t1/2 = 256 minutes,
k = 0.693 / t1/2
= 0.693 / 256
= 2.707 × 10-3 min-1 k = 4.51 × 10-5s–1
Substitute k = 4.51 × 10-5s–1 in eqn 2,
log 4.51 × 10-5 s–1 = 14.34 – 1.25 × 104K/T
log(0.654-5) = 14.34– 1.25 × 104K/T T = 1.25 × 104/[ 14.34- log(0.654-5)] T = 668.9K or T = 669 K
Exercise Q 4.28 The decomposition of A into product has value of k as 4.5× 103 s–1 at 10°C and energy of activation 60 kJ mol–1. At what temperature would k be 1.5 × 104s–1?
From Arrhenius equation, we obtain
Also, k1 = 4.5 × 103 s -1
T1 = 273 + 10 = 283 K
k2 = 1.5 × 104 s -1
Ea = 60 kJ mol -1 = 6.0 × 104 J mol -1
Then,
→ 0.5229 = 3133.627 × (T2-283)/(283 × T2)
→ 0.0472T2 = T2-283 T2 = 297K or T2 = 240 C
Exercise Q 4.29 The time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K. If the value of A is 4 × 1010s –1, calculate k at 318K and Ea.
A 4.29
We know, time t = (2.303/k) × log([R]0/[R])
Where, k- rate constant [R]0-Initial concentration
[R]-Concentration at time ‘t’
At 298K, If 10% is completed, then 90% is remaining. t = (2.303/k) × log ([R]0/0.9[R]0)
t = (2.303/k) × log (1/0.9) t = 0.1054 / k
At temperature 308K, 25% is completed, 75% is remaining t’ = (2.303/k’) × log ([R]0/0.75[R]0)
t’ = (2.303/k’) × log (1/0.75) t’ = 2.2877 / k'
But, t = t’
0.1054 / k = 2.2877 / k' k' / k = 2.7296
From Arrhenius equation, we obtain log k2/k1 = (Ea / 2.303 R) × (T2 - T1) / T1T2
Substituting the values,
Ea = 76640.09 J mol-1 or 76.64 kJ mol-1 We know, log k = log A –Ea/RT
Log k = log(4 × 1010)-(76.64kJ mol-1/(8.314 × 318) Log k = -1.986
∴k = 1.034 x 10-2 s -1
Exercise Q 4.30 The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
A 4.30
Given, k2 = 4k1, T1 = 293K and T2 = 313K
We know, From Arrhenius equation, we obtain
On solving we get,
Ea = 58263.33 J mol-1 or 58.26 kJ mol-1
News & Updates
Chemistry Ncert Solutions Class 12th Exam