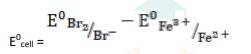NCERT Class 12 Solution Electrochemistry: Electrochemistry is the study of the production of electricity from energy released during spontaneous chemical reactions and the use of electrical energy to bring about non-spontaneous chemical transformations. The electrochemistry chapter is of importance both for board exams as well as competitive exams like JEE Mains.
The study of electrochemistry is important for creating new technologies that are ecofriendly. A large number of metals, sodium hydroxide, chlorine, fluorine and many other chemicals are produced by electrochemical methods. Batteries and fuel cells convert chemical energy into electrical energy and are used on a large scale in various instruments and devices. The reactions carried out electrochemically can be energy efficient and less polluting.
To help students study NCERT Class 12 Chemistry Electrochemistry chapter, provided here are solutions of all questions. These NCERT Chemistry class 12 Electrochemistry solutions have been prepared by subject experts and are easy to understand.
NCERT Class 12 Electrochemistry Topics
Candidates can check here the list of all topics that are covered under electrochemistry chapter of NCERT chemistry class 12
- Electrochemical Cells
- Galvanic Cells
- Measurement of Electrode Potential
- Nernst Equation
- Equilibrium Constant from Nernst Equation
- Electrochemical Cell and Gibbs Energy of Reaction
- The conductance of Electrolytic Solutions
- Measurement of the Conductivity of Ionic Solutions
- Variation of Conductivity and Molar Conductivity with Concentration
- Electrolytic Cells and Electrolysis
- Products of Electrolysis
- Batteries
- Primary Batteries
- Secondary Batteries
- Fuel Cells
- Corrosion
NCERT Chemistry Class 12th Solution PDF - Electrochemistry Chapter Download
Electrochemistry is an important chapter for the students because it forms the foundation of various other concepts. We are providing the solutions for all the NCERT questions given in this chapter for the students. The students can download the NCERT solutions for Electrochemistry Chapter here for free.
Download Here:NCERT Solution for Class XII Chemistry Electrochemistry PDF
Explore exams which ask questions on Chemistry Ncert Solutions Class 12th
Select your preferred stream
Electrochemistry Solutions and FAQs
Intext Q 3.1 How would you determine the standard electrode potential of the system Mg2+|Mg?
A 3.1 To determine the standard electrode potential of the system Mg2+|Mg, connect it to the standard hydrogen electrode (SHE). Keep the Mg2+|Mg system as cathode and SHE as cathode. This is represented as shown below.
Pt(s) | H2(g, 1 bar)| H+ (aq, 1 M) ||Mg2+ (aq, 1M)| Mg
The electrode potential of a cell is given by
E⊖ = E⊖R – E⊖L
Where,
E⊖R- Potential of the half-cell in the right side of the above representation
E⊖L- Potential of the half-cell in the left side of the above representation
It is to be noted that the potential of the standard hydrogen electrode is zero.
Therefore, E⊖L = 0
E⊖ = E⊖R – 0
⇒ E⊖ = E⊖R
Intext Q 3.2 Can you store copper sulphate solutions in a zinc pot?
A 3.2 NO, because Zn is very reactive with Cu. It reacts with copper sulphate to form zinc sulphate i.e., Zn displaces Cu and metallic Cu is also formed.
The reaction is given as:
Zn + CuSO4 ⇒ ZnSO4 + Cu
Intext Q 3.3 Consult the table of standard electrode potentials and suggest three substances that can oxidise ferrous ions under suitable conditions.
A 3.3 :For a substance to oxidise Fe2+ to Fe3+ ion, it must have high reduction potential than Fe3+. The reduction potential of Fe3+ to Fe2+ reaction is 0.77V, the substances which have reduction potentials higher than this value will oxidise Fe2+ ions. Comparing the values, from the table:
Intext Q 3.4 Calculate the potential of hydrogen electrode in contact with a solution whose pH is 10.
A 3.4 Given:
For hydrogen electrode, pH = 10
n = 1
(n = moles of e- from balanced redox reaction)
On using the formula [H+] = 10– pH
⇒ [H+] = 10 − 10 M
We know,
Intext Q 3.5 Calculate the emf of the cell in which the following reaction takes place: Ni(s) + 2Ag+ (0.002 M) → Ni2+ (0.160 M) + 2Ag(s) Given that E(cell) V = 1.05 V
A 3.5 Given:
[Ag+] = 0.002 M
[Ni2+] = 0.160 M
n = 2
(n = moles of e- from balanced redox reaction)
E0cell= 1.05 V
Now, using the Nernst equation we get,
Intext Q 3.6 The cell in which the following reaction occurs: ( ) ( ) ( ) ( ) 3 2 2Fe 2I 2Fe I aq aqaq 2 s + − + + → + has 0 Ecell = 0.236 V at 298 K. Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction
A 3.6 Given:
2Fe3+(aq) + 2I- (aq) → 2Fe2+(aq) + I2(s)
E0cell = 0.236V
n = moles of e- from balanced redox reaction = 2
F = Faraday's constant = 96,485 C/mol
T = 298 K.
Using the formula, we get
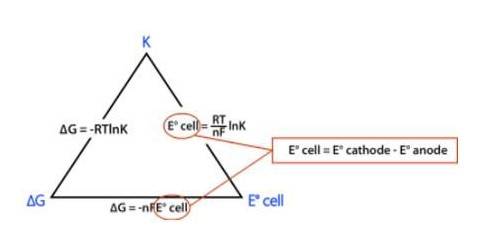
∆rG0 = – nFE0cell
⇒ ∆rG0 = – 2 × FE0cell
⇒ ∆rG0 = −2 × 96485 C mol-1 × 0.236 V
⇒ ∆rG0 = −45540 J mol-1
⇒ ∆rG0 = −45.54 kJ mol-1
Now,
∆rG0 = −2.303RT log Kc
Where, K is the equilibrium constant of the reaction
R is the gas constant; R = 8.314 J-mol-C-1
⇒ −45540 J mol-1 = –2.303× (8.314 J-mol-C-1)× (298 K) × (log Kc)
Solving for Kc we get,
⇒ logKc = 7.98
Taking antilog both side, we get
⇒ Kc = Antilog (7.98)
⇒ Kc = 9.6 × 107
Trick to remember
Intext Q 3.7 Why does the conductivity of a solution decrease with dilution?
A 3.7 The conductivity of a solution depends on the amount of ions present per volume of the solution. When diluted, the concentration of the ions decreases which implies that the number of ions per volume decreases thus, in turn, conductivity decreases.
Intext Q 3.8 Suggest a way to determine the Λm ° value of water
A 3.8
Intext Q 3.9 The molar conductivity of 0.025 mol L^–1 methanoic acid is 46.1 S cm^2 mol^–1 . Calculate its degree of dissociation and dissociation constant. Given λ0 (H+ ) = 349.6 S cm2 mol^–1 and λ 0 (HCOO– ) = 54.6 S cm^2 mol^–1 . s
A 3.9 C = 0.025 mol L-1
Am = 46.1 Scm2 mol L-1
λ0 (H+) = 349.6 Scm2 mol L-1
λ0 (HCOO-) = 54.6 Scm2 mol L-1
Λ0m (HCOOH) = Λ0(H+) + Λ0(HCOO-)
= 349.6 + 54.6
= 404.2 S cm2 mol L-1
Now, the degree of dissociation:
Intext Q 3.10 If a current of 0.5 ampere flows through a metallic wire for 2 hours, then how many electrons would flow through the wire?
A 3.10 Current I = 0.5A
Time t = 2hrs = 2×60×60 = 7200 seconds
Charge Q = I × t
Q = 0.5×7200 = 3600 C
Charge carried by 1 mole of electrons (6.023×1023electrons) is equal to 96487C.
No of electrons = 6.023×1023 × 3600/96487
No of electrons = 2.25×1022 electrons
Intext Q 3.11 Suggest a list of metals that are extracted electrolytically.
A 3.11 Metals with greater reactivity can be extracted electrolytically. Sodium, potassium, calcium, lithium, magnesium, aluminium which are present in the top of the reactivity series are extracted electrolytically.
Intext Q 3.12 Consider the below reaction. What is the quantity of electricity in coulombs needed to reduce 1 mol of Cr2O7 2–?
Cr2O72– + 14H+ + 6e–⇒ 2Cr3+ + 7H2O
A 3.12
Cr2O72– + 14H+ + 6e–⇒ 2Cr3+ + 7H2O
For reducing one mole of Cr2O72–, 6 mole of electrons are required. Hence, 6 faraday charge is needed. Hence, 6F = 6×96487 = 578922 C. Thus, the quantity of electricity is needed is 578922 C.
Intext Q 3.13 Write the chemistry of recharging the lead storage battery, highlighting all the materials that are involved during recharging.
A 3.13
Anode: Lead (Pb)
Cathode: a grid of lead packed with lead oxide (PbO2)
Electrolyte: 38% solution of sulphuric acid (H2SO4)
The cell reactions are as follows :
Pb (s) + SO2-4(aq) ⇒ PbSO4 (s) + 2e- (anode)
PbO2(s) + SO2-4(aq) + 4H+(aq) +2e-⇒ PbSO4(s) +2H2O(l) (cathode)
Pb(s) + PbO2(s) +2H2SO4(aq)⇒ 2PbSO4(s) +2H2O(l)
(overall cell reaction)
On charging, all these reactions will be reversed.
Intext Q 3.14 Suggest two materials other than hydrogen that can be used as fuels in fuel cells.
A 3.14 Suggest two materials other than hydrogen that can be used as fuels in fuel cells.
Intext Q 3.15 Explain how rusting of iron is envisaged as setting up of an electrochemical cell.
A 3.15 In the corrosion reaction, due to the presence of air and moisture, oxidation takes place at a particular point of an object made of iron. That spot behaves as the anode. The reaction at the anode is given by,
Fe(s) ⇒ Fe2+ (aq) + 2e-
Electrons released at the anodic spot move through the metal and go to another spot of the object, wherein presence of H+ ions, the electrons reduce oxygen. This spot behaves as the cathode. These H+ ions come either from H2CO3, which are formed due to the dissolution of carbon dioxide from the air into water. The cathodic reaction is given by
O2(air) + 4Haq++4e-⇒ 2H O
The overall reaction is given by,
2Fe(s) + O2(air) + 4H(aq)+⇒ 2Fe2++2H2O
Exercise Q 3.1 Arrange the following metals in the order in which they displace each other from the solution of their salts. Al, Cu, Fe, Mg and Zn.
A 3.1 The order in which the given metals displace each other from the solution of their salts is given by,
Mg>Al> Zn> Fe> Cu
A metal of stronger reducing power displaces another metal of weaker reducing power from its solution of salt. The order of increasing the reducing power of given metals is Cu< Fe< Zn< Algiven metals displace each other from the solution of their salts is given by, Mg>Al> Zn> Fe> Cu. This is hence arranged in decreasing order of its reactivity
Exercise Q 3.2 Given the standard electrode potentials, (given below) Arrange these metals in their increasing order of reducing power.
K + /K = –2.93V, Ag+ /Ag = 0.80V, Hg2+/Hg = 0.79V Mg2+/Mg = –2.37 V, Cr3+/Cr = – 0.74V
A 3.2 Reducing power of metals increase with the decrease of reduction potential. Hence, the increasing order of reducing power will be as,
Ag < Hg < Cr < Mg < K
When the reduction potential is lower, the element has more tendency to get oxidized and thus more will be reducing power. The metal that has more negative electrode potential will be the one with more reducing power. Thus, here potassium (K) has the highest reducing power among the given elements.
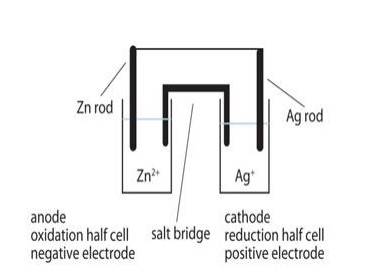
Exercise Q 3.3 Depict the galvanic cell in which the reaction Zn(s)+2Ag+ (aq) →Zn2+(aq)+2Ag(s) takes place. Further show: (i) Which of the electrode is negatively charged? (ii) The carriers of the current in the cell. (iii) Individual reaction at each electrode.
A 3.3 The galvanic cell corresponding to the given redox reaction can be represented as:
Zn|Zn2+(aq)||Ag +(aq)|Ag
- 1) Zn electrode (anode) is negatively charged because, at this electrode, Zn is oxidized to Zn2+, causing electron accumulation at the
- 2) Electrons (ions) are the carriers of the current in the cell and in the external circuit, current flows from Ag (cathode) to Zn(anode) which is normally opposite to the electron flow which is from anode to cathode.
- 3) At anode:
Zn(s)⇒ Zn2 + (aq) + 2e– At cathode:
Ag + (aq) + e –⇒ Ag(s)
Exercise Q 3.4 Calculate the standard cell potentials of galvanic cell in which the following reactions take place: (i) 2Cr(s) + 3Cd2+(aq) → 2Cr3+(aq) + 3Cd (ii) Fe 2+(aq) + Ag+ (aq) → Fe3+(aq) + Ag(s) Calculate the ∆rG⊖ and equilibrium constant of the reactions.
A 3.4 (1) Known - E0Cr3+/Cr = - 0.74 V
E0 cd2+ = - 0.40 V
∆rG0 = ? K = ?
The galvanic cell of the given reaction is written as - Cr(s)|Cr3+(aq)|| Cd2+(aq)|Cd(s)→ Reaction 1
Hence, the standard cell potential is given as, E0 = ER0 - EL0
= - 0.40 - (- 0.74)
∴ E0 = + 0.34 V
To calculate the standard Gibb’s free energy, ∆rG0, we use,
∆rG0 = - nE0F → Equation 1
wherenF is the amount of charge passed and E0 is the standard reduction electrode potential. Substituting n = 6 (no. of e - involved in the reaction 1), F = 96487 C mol-1,
E0 = + 0.34 V in Equation 1, we get,l
∆rG0 = - 6×0.34V×96487 C mol-1
= - 196833.48 CV mol-1
= - 196833.48 J mol-1
∴ ∆rG0 = - 196.83348 kJ mol-1
To find out the equilibrium constant, K, we use the formula,
log K =n E0 / 0.0591
=6 X 0.3 V / 0.0591
log K = 34.5177
K = antilog 34.5177
∴ K = 3.294 × 1034
The standard Gibb’s free energy, ∆rG0 is - 196.83348 kJ mol –1 and equilibrium constant, K is 3.294 × 1034
(2) Known -
E0 Fe3+ / Fe2+ = 0.77V
E0 Ag+ / Ag = 0.80 V
∆rG0 = ? K = ?
The galvanic cell of the given reaction is written as - Fe2+(aq)|Fe3+(aq)|| Ag +(aq)|Ag(s)→ Reaction 1
Hence, the standard cell potential is given as, E0 = ER0 - EL0
= 0.80 - (0.77)
∴ E0 = + 0.03 V
To calculate the standard Gibb’s free energy, ∆rG0, we use,
∆rG0 = - nE0F → Equation 1
wherenF is the amount of charge passed and E0 is the standard reduction electrode potential.
Substituting n = 1 (no. of e - involved in the reaction 1), F = 96487 C mol-1, E0 = + 0.03V in Equation 1, we get,
∆rG0 = - 1×0.03V×96487 C mol-1
= - 2894.61 CV mol -1
= - 2894.61 J mol-1
∴ ∆rG0 = - 2.89461 kJ mol-1
To find out the equilibrium constant, K, we use the formula,
log K =n E0 / 0.0591
=1 X 0.03 V / 0.0591
log K = 0.5076
K = Antilog 0.5076
∴ K = 3.218
The standard Gibb’s free energy, ∆rG0 is - 2.89461 kJ mol –1 and equilibrium constant, K is 3.218
Exercise Q 3.5 Write the Nernst equation and emf of the following cells at 298 K:
(i) Mg(s)|Mg 2+(0.001M)||Cu2+(0.0001 M)|Cu(s) (ii) Fe(s)|Fe 2+(0.001M)||H+ (1M)|H2 (g)(1bar)| Pt(s) (iii) Sn(s)|Sn2+(0.050 M)||H+ (0.020 M)|H2 (g) (1 bar)|Pt(s) (iv) Pt(s)|Br – (0.010 M)|Br2 (l )||H+ (0.030 M)| H2 (g) (1 bar)|Pt(s).
A 3.5 Ecell = ?
(i) Mg + Cu2+ → Mg2+ + Cu (n = 2)
E0 Cu2+ / Cu+ = 0.34V
E0 Mg 2+ / Mg = - 2.37 V
Ecell0 = ER0-EL0
Ecell0 = 0.34 - ( - 2.37) → Equation 1
Using Nernst equation, we get,
Substituting Equation 1 in equation 2, we get,
∴ Ecell = 0.34 - ( - 2.37) - 0.0591 / 2 log 10 -3/ 10-4
= 2.71 - 0.0591 / 2 log 10
= 2.71 - 0.02955
∴ Ecell = 2.68 V
The e.m.f of the cell, Ecell is 2.68 V
ii) Fe + 2H + → Fe2+ + H2 (n = 2)
E0 H+ / H2 = 0V
E0 Fe 2+ / Fe = - 0.44 V
Ecell0 = ER0-EL0
Ecell0 = 0 - ( - 0.44) → Equation 1
Using Nernst equation, we get,
∴ Ecell = 0.5287 V
The e.m.f of the cell, Ecell is 0.5287 V
iii) Sn + 2H + → Sn2+ + H2 (n = 2)
Ecell0 = 0 - ( - 0.14) → Equation 1
Using Nernst equation, we get,
Exercise Q 3.6 In the button cells widely used in watches and other devices the following reaction takes place: Zn(s) + Ag2O(s) + H2O(l) → Zn2+(aq) + 2Ag(s) + 2OH– (aq) Determine ∆r G ⊖ and E ⊖ for the reaction.
A 3.6 Given - Zn → Zn2+ + 2e - , E0 = 0.76V (anode)
Ag2O + H2O + 2e - →2Ag + 2OH - , E0 = 0.344V (cathode), n = 2
ΔrG0 = ?
Ecell0= ?
Zn is oxidized and Ag2O is reduced.
Hence, the standard cell potential, Ecell0 is given as,
Ecell0 = ER0 - EL0
E0 cell = 0.344 + 0.76
∴ E0cell = 1.104 V
To calculate the standard Gibb’s free energy, ∆rG0, we use,
∆rG0 = - nE0F → Equation 1
= - 2×96487×1.104 J
= - 213043.296 J
∴ ∆rG0 = - 2.13×105 J
The standard cell potential, E0cell is 1.104 V and the standard Gibb’s free energy, ∆rG0 is - 2.13×105 J
Exercise Q 3.7 Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration.
A 3.7 The conductivity of a solution is defined as the conductance of one unit volume of solution kept between two platinum electrodes with a unit area of cross-section and at a distance of unit length.The molar conductivity of the solution is defined as the conducting power of all the ions produced by
one gram mole of an electrolyte in a solution. It is denoted by ∧m.
The conductivity of a solution (both for strong and weak electrolytes) always decreases with the decrease in concentration of the electrolyte i.e., on dilution. This pattern is seen because the number of ions per unit volume that carry the current in the solution decreases on dilution. The molar conductivity of the solution increases with the decrease in concentration of the electrolyte. This is because both the number of ions as well as mobility of ions increases with dilution.
Exercise Q 3.8 The conductivity of 0.20 M solution of KCl at 298 K is 0.0248 S cm^–1. Calculate its molar conductivity
A 3.8 Given -
Molarity, C = 0.20 M
Electrolytic conductivity of a solution, κ = 0.0248 S cm-1
Molar conductivity = ?
Molar conductivity, ∧m = K/C X 1000 S cm2 mol-1
=0.0248S cm-1 X 1000 Cm3L-1 / 0.20 mol L-1
∴ ∧m = 124 S cm2 mol-1
Molar conductivity(∧m) of 0.20 M solution of KCl at 298 K is 124 S cm2 mol-1
Exercise Q 3.9 The resistance of a conductivity cell containing 0.001M KCl solution at 298 K is 1500 Ω. What is the cell constant if conductivity of 0.001M KCl solution at 298 K is 0.146 × 10^–3 S cm^–1 .
A 3.9 Given -
Resistance of a conductivity cell, R = 1500 Ω
Electrolytic conductivity of a solution, κ = 0.146 × 10-3 S cm-1
Cell constant = ?
Conductivity, κ = cell constant/resistance
Cell constant = κ × R
= 0.146 × 10-3 S cm-1×1500 Ω
Cell constant = 0.219 cm-1
The cell constant of the cell containing 0.001M KCl solution at 298 K is 0.219 cm-1
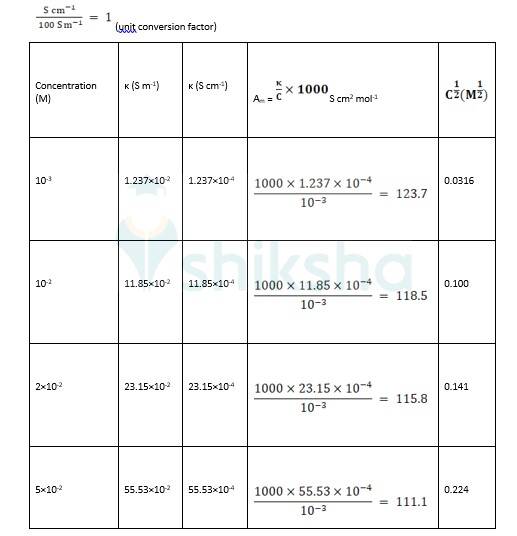
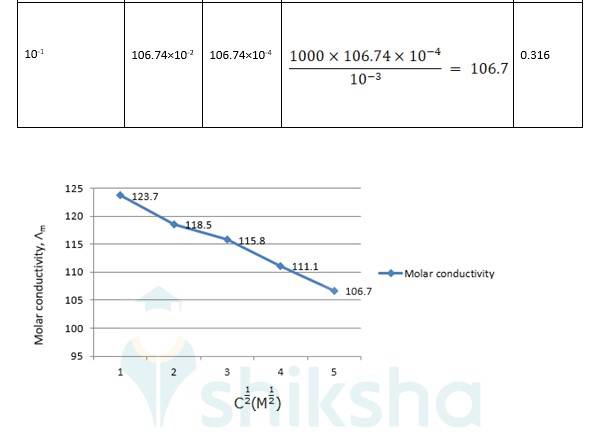
Exercise Q 3.10 3.10 The conductivity of sodium chloride at 298 K has been determined at different concentrations and the results are given below: Concentration/M 0.001 0.010 0.020 0.050 0.100 102 × κ/S m^–1 1.237 11.85 23.15 55.53 106.74 Calculate Λm for all concentrations and draw a plot between Λm and c½ . Find the value of 0 Λm
A 3.10
?0 R = Intercept on the ? axis = 124.0 S cm2 mol-1, which is obtained by extrapolation to zero concentration.
Exercise Q 3.11 Conductivity of 0.00241 M acetic acid is 7.896 × 10–5 S cm–1. Calculate its molar conductivity. If 0 Λm for acetic acid is 390.5 S cm2 mol –1, what is its dissociation constant?
A 3.11 Given -
Molarity, C = 0.00241 M
Conductivity, κ = 7.896 × 10–5 S cm–1
Molar conductivity, ?m = ?
?0m for acetic acid = 390.5 S cm2mol–1
Molar conductivity, ?m = k/c X 1000 S cm2 mol-1
= 7.896 X 10–5 S cm–1X 1000 cm3 L-1 / 0.00241 mol L-1
∴ ?m = 32.76 S cm2 mol-1
To calculate the dissociation constant, Ka, we use
Ka = → Equation 1
Here, we need to find the value of α (degree of dissociation), by the formula,
The molar conductivity, ?m is 32.76 S cm2 mol-1 and the dissociation constant, Ka is 1.86×10-5
Exercise Q 3.12 How much charge is required for the following reductions: (i) 1 mol of Al3+ to Al? (ii) 1 mol of Cu2+ to Cu? (iii) 1 mol of MnO4 – to Mn2+ ?
A 3.12 The electrode reaction is given as,
Al3+ (aq) + 3e- → Al(s)
∴ The quantity of charge required for the reduction of 1 mol of Al3+ = 3F
= 3×96487 C
= 289461 C
The electrode reaction is given as,
Cu2+ (aq) + 2e- → Cu(s)
∴ The quantity of charge required for the reduction of 1 mol of Cu2+ = 2F
= 2×96487 C
= 192974 C
The electrode reaction is given as, MnO4→ Mn2+
i.e., Mn7+ + 5e - → Mn2+
∴ The quantity of charge required for the reduction of 1 mol of Mn7+ = 5F
= 5×96487 C
= 482435 C
Exercise Q 3.13 How much electricity in terms of Faraday is required to produce (i) 20.0 g of Ca from molten CaCl2?
A 3.13 (i) Ca2+ + 2e- → Ca
⇒ Here, 1 mole of Ca, i.e., 40g of Ca requires = 2 F electricity (F if Faraday)
∴ 20g of Ca requires = 20X2/40
= 1 F of electricity
Electricity in terms of Faraday required to produce 20.0 g of Ca from molten CaCl2 is 1 F of electricity.
(ii) Al3+ + 3e- → Al
⇒ 1 mole of Al, i.e., 27g of Al requires = 3 F electricity (F if Faraday)
∴ 40.0 g of Al will require = 3/27 X 40
= 4.44 F of electricity
Electricity in terms of Faraday required to produce 40.0 g of Al from molten Al2O3 is 4.44 F of electricit
Exercise Q 3.14 How much electricity is required in coulomb for the oxidation of (i) 1 mol of H2O to O2 ? (ii) 1 mol of FeO to Fe2 O3 ?
A 3.14 The electrode reaction for 1 mole of H2O is given as,
H2O → H2 + 1/2O2
i.e., O2- →1/2 O2 + 2e -
∴ The quantity of electricity required = 2F
= 2×96487 C
= 192974 C
The quantity of electricity required in coulomb for the oxidation of 1 mol of H2O to O2 is 192974 C
- (ii) The electrode reaction for 1 mole of FeO is
FeO + 1/2 O2 → 1/2 Fe2O3
i.e., Fe2+ → Fe3+ + e -
∴ The quantity of electricity required = 1F
= 1×96487 C
= 96487 C
The quantity of electricity required in coulomb for the oxidation of 1 mol of FeO to Fe2O3 is 96487 C
Exercise Q 3.15 A solution of Ni(NO3)2 is electrolysed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?
A 3.15 Quantity of electricity passed = 5 A × (20 × 60 sec)
= 6000 C ⇒ Equation 1
The electrode reaction is written as,
Ni2+ + 2e → Ni
Thus, the quantity of electricity required = 2F
= 2×96487 C
= 192974 C
∵ 192974 C of electricity deposits 1 mole of Ni, which is 58.7 g ⇒ Equation 2
Thus, equating equations 1 and 2, we get
192974 C of electricity deposits = 58.7 g
6000 C of electricity will deposit = 58.7 X 6000 / 192974
= 1.825g of Ni
The mass of Ni deposited at the cathode is 1.825g of Ni
Exercise Q 3.16 Three electrolytic cells A, B, C containing solutions of ZnSO4 , AgNO3 and CuSO4 , respectively are connected in series. A steady current of 1.5 amperes was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?
A 3.16 Equivalent weight is Ag, EAg = 180/1 = 180
Equivalent weight is Cu, ECu = 63.5 / 2 = 31.75
Equivalent weight is Zn, EZn= 65/2 = 32.5
Using Faraday’s second law of electrolysis, to find the mass of Cu and Zn, we use Equation 1,
∴ WZn = 0.436 g
To find the time of current flow, using Faraday’s first law of electrolysis we get,
M = Z ×I ×t ⇒ Equation 2
∵ Z = Equivalent Weight / 96487 , Equation 2 becomes,
M = 108 / 96487 X 1.5 X t
t = 1.45 X 96487 / 108X 1.5
t = 864 seconds.
The time of current flow, t = 864 seconds, the mass of Cu is 0.426 g and mass of Zn is 0.436 g
Exercise Q 3.17 Using the standard electrode potentials given in Table 3.1, predict if the reaction between the following is feasible: (i) Fe 3+(aq) and I – (aq) (ii) Ag+ (aq) and Cu(s) (iii) Fe3+ (aq) and Br– (aq) (iv) Ag(s) and Fe 3+ (aq) (v) Br 2 (aq) and Fe2+ (aq).
A 3.17 The electrode reaction is written as,
2Fe3+ + 2I - → 2Fe2+ + I2
= 0.54V - 0.77V
∴ E0cell = - 0.23 V
It is not feasible, as E0cell is negative, ∴ ∆G0 is positive.
- The electrode reaction is written as,
- 2Ag+ (aq) + Cu(s)→ Cu2+ (aq) + Ag(s)
= + 0.80V - 0.34V
∴ E0cell = 0.46V
It is feasible, as Ecell 0 is positive, ∴ ∆G0 is negative.
- (iii) The electrode reaction is written as,
- 2Fe3+ (aq) + 2Br- (aq)→ 2Fe2+ (aq) + Br2
= 0.77V - 1.09V
∴ E0cell = - 0.32 V
It is not feasible, as E0cell is negative, ∴ ∆G0 is positive.
- (iv) The electrode reaction is written as,
- Ag(s) + Fe3+ (aq) → Fe2+ (aq) + Ag+ (aq)
= 0.77V - 0.80V
∴ E0cell = - 0.03
It is not feasible, as E0cell is negative, ∴ ∆G0 is positive.
- (v) The electrode reaction is written as,
- Br2 + 2Fe2+ (aq) → 2Br- (aq) + 2Fe3+ (aq)
= 1.09V - 0.77V
∴ E0cell = 0.32 V
It is feasible, as Ecell0 is positive, ∴ ∆G0 is negative.
Exercise Q 3.18 Predict the products of electrolysis in each of the following: (i) An aqueous solution of AgNO3 with silver electrodes. (ii) An aqueous solution of AgNO3 with platinum electrodes. (iii) A dilute solution of H2SO4 with platinum electrodes. (iv) An aqueous solution of CuCl2 with platinum electrodes.
A 3.18 Given -
All the ions are in aqueous state.
Reaction in solution:
AgNO3(s) + aq → Ag + + NO3-
H2O → H + + OH -
At cathode:
Ag + (aq) + e - →Ag(s)
Ag + ions have lower discharge potential than H + ions. Hence, Ag + ions get deposited as Ag in preference to H + ions.
At anode:
Ag(s)→ Ag + (aq) + e -
As Ag anode is attacked by NO3- ions, Ag of the anode will dissolve to form Ag + ions in the aqueous solution.
(ii) Reaction in solution:
AgNO3(s) + aq → Ag + + NO3-
H2O óH + + OH -
At cathode:
2Ag +(aq) + 2e - →2Ag(s)
Ag + ions have lower discharge potential than H + ions. Hence, Ag + ions get deposited as Ag in preference to H + ions.
At anode:
2OH- (aq) → O2(g) + 2H+ (aq) + 4e -
As anode is not attackable, out of OH - and NO3- ions, OH - having lower discharge potential, will be discharged in preference to NO3- ions. These then decompose to give out O2.
(iii) Reaction in solution
H2SO4(aq) → 2H+ (aq) + SO2-4 (aq)
At cathode:
2H + (aq) + 2e - →H2(g)
At anode:
2OH- (aq) → O2(g) + 2H+ (aq) + 4e -
∴ H2 gas is evolved at cathode and O2(g) is evolved at anode.
(iv) Reaction in solution: CuCl2(s) + aq → Cu2+ (aq) + Cl- (aq)
H2O óH + + OH -
At cathode:
Cu2+ (aq) + 2e - →Cu(g)
At anode:
2Cl- (aq) - 2e- → Cl2(g)
∴ Cu will be deposited at cathode and Cl2 gas will be liberated at anode.
News & Updates
Chemistry Ncert Solutions Class 12th Exam


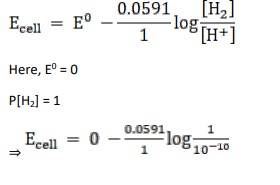
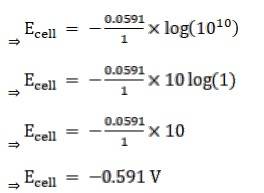



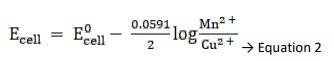
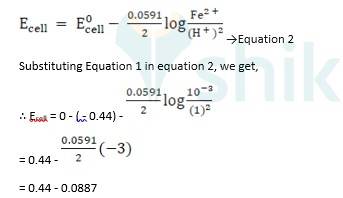
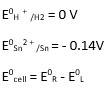

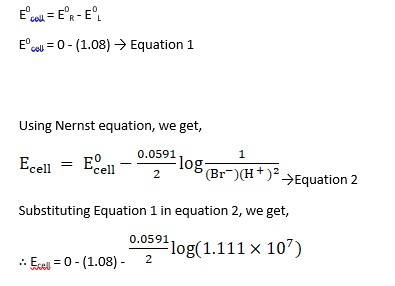
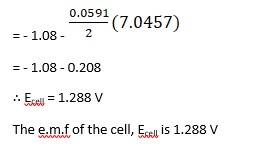

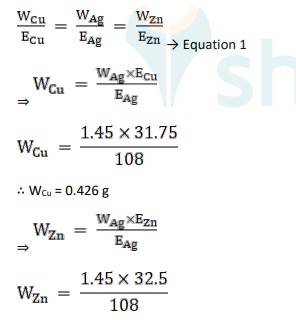
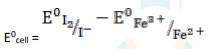
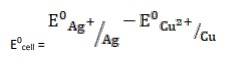
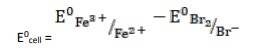 k
k