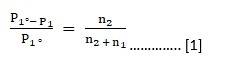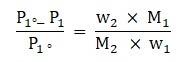NCERT Chemistry Class 12 Solutions: A solution is a homogeneous mixture of two or more substances. Solutions are classified as solid, liquid and gaseous solutions. The concentration of a solution is expressed in terms of mole fraction, molarity, molality and percentages.
In this chapter of NCERT class 12 Chemistry Solution, students will study various properties of solutions, types of solutions and solubility. It is a very important chapter from JEE Main point of view as questions are asked every year from this chapter. Also in class 12 board exams, questions are asked from NCERT Chemistry Solution chapter.
Candidates are provided here detailed NCERT Chemistry Class 12 Solution of Solutions chapter prepared by subject experts. It will help students easily learn all the important concepts and score good marks in the exam.
- NCERT Class 12 Chemistry Solution Topics
- NCERT Chemistry Class 12th Solution PDF - Solutions Chapter Download
- Solutions and FAQs
NCERT Class 12 Chemistry Solution Topics
Candidates can check below the list of topics that are covered in NCERT chemistry class 12 solution chapter
- Types of Solutions
- Expressing Concentration of Solutions
- Solubility
- The solubility of a Solid in a Liquid
- The solubility of a Gas in a Liquid
- Vapour Pressure of Liquid Solutions
- Vapour Pressure of Liquid-Liquid Solutions
- Raoult’s Law as a Special Case of Henry’s Law
- Vapour Pressure of Solutions of Solids in Liquids
- Ideal and Nonideal Solutions
- Ideal Solutions
- Non-ideal Solutions
- Colligative Properties and Determination of Molar Mass
- Relative Lowering of Vapour Pressure
- Elevation of Boiling Point
- Depression of Freezing Point
- Osmosis and Osmotic Pressure
- Abnormal Molar Masses
NCERT Chemistry Class 12th Solution PDF - Solutions Chapter Download
Solutions is an important chapter for the students because it forms the foundation of various other concepts. We are providing the solutions for all the NCERT questions given in this chapter for the students. The students can download the NCERT solutions for solutions Chapter here for free.
Download Here:NCERT Solution for Class XII Chemistry Solutions Chapter
Explore exams which ask questions on Chemistry Ncert Solutions Class 12th
Select your preferred stream
Solutions and FAQs
Intext Q 2.1 Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (CCl4) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
A 2.1 Mass of Solution = Mass of Benzene + Mass of Carbon Tetrachloride
= 22 g + 122 g = 144 g
Mass percentage of Benzene = Mass of Benzene / Mass of Solution X 100 = 22/144 X 100 = 15.28%
Mass percentage of CCl4 = Mass of CCl4 / Mass of Solution X 100 = 122/144 X 100 = 84.72%
Intext Q 2.2 Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
Let the total mass of the solution be 100 g and the mass of benzene be 30 g.
∴ Mass of carbon tetrachloride = (100 - 30) g = 70 g
Molar mass of benzene (C6H6) = (6 × 12 + 6 × 1) g mol -1
= 78 g mol -1
∴ Number of moles of C6H6 =30/78 mol
= 0.3846 mol
Molar mass of carbon tetrachloride (CCl4) = 1 × 12 + 4 × 35.5
= 154 g mol -1
∴ Number of moles of CCl4 = 70/154 mol
= 0.4545 mol
Thus, the mole fraction of C6H6 is given as:
Number of moles of C6H6 / Number of moles of C6H6 + Number of moles of CCl4
= 0.3846 / (0.3846 + 0.4545)
Intext Q 2.3 Calculate the molarity of each of the following solutions: (a) 30 g of Co(NO3)2. 6H2O in 4.3 L of solution (b) 30 mL of 0.5 M H2SO4 diluted to 500 mL.
- A 2.3 Molarity = Moles of Solute / Volume of Solution in liter
- (a) Given, In 4.3 L of solution there is 30 g of Co(NO3)2. 6H2O
Molar mass of Co(NO3)2.6H2O = (1 × 59 + 2 × (1 × 14 + 3 × 16) + 6 × 18)
= 291 g/mol.
∴ Moles = Given Mass / Molar Mass = 30/291 = 0.103 mol.
Now, Molarity = 0.103 mol / 4.3 L
= 0.023 M
- (b) Given, 30 mL of 0.5 M H2SO4 diluted to500 mL.
In 1000 mL of 0.5 M H2SO4, number of moles present is 0.5 mol.
∴ In 30 mL of 0.5 M H2SO4, number of moles present = 30X 0.5 / 1000 mol.
= 0.015 mol.
∴ Molarity = 0.015 mol / 0.5L
= 0.03 M.
Intext Q 2.4 Calculate the mass of urea (NH2CONH2) required in making 2.5 kg of 0.25 molal aqueous solution.
A 2.4, 2.5 kg of 0.25 molal aqueous solution.
Molar mass of urea (NH2CONH2) = (2 (1 × 14 + 2 × 1) + 1 × 12 + 1 × 16)
= 60 g/mol
1000 g of water contains 0.25 mol = (0.25 × 60) g of urea.
= 15 g of urea.
Means, 1015 g of solution contains 15 g of urea
Therefore,
2500 g of solution contains = 15 X 2500 / 1015
= 36.95 g
Hence, mass of urea required is 37 g (approx).
Intext Q 2.5 Calculate (a) molality (b) molarity and (c) mole fraction of KI if the density of 20% (mass/mass) aqueous KI is 1.202 g mL^-1 .
A 2.5 Molality, also called molal concentration, is a measure of the concentration of a solute in a solution in terms of amount of substance in a specified amount of mass of the solvent. Molar mass of KI = 39 + 127 = 166 g/mol.
20% aqueous solution of KI means 200 g of KI is present in 1000 g of solution. Therefore,
Molality = Moles of KI / Mass of Water in kg
= (200/166) / (0.8) = 1.506 m
(b) Molarity is the concentration of a solution expressed as the number of moles of
solute per litre of solution.
Given,
Density of the solution = 1.202 g/mL
Volume of 100 g solution = mass/ density
= 100/1.202
= 83.19 mL
Therefore, molarity = 20/166 mol/ 83.19 × 10-3 L
= 1.45 M
∴ Molarity of KI = 1.45M
(c) Molar mass of KI = 39 + 127 = 166 g/mol.
Moles of KI = 20/166 = 0.12 mol
Moles of water = 80/18 = 4.44 mol
Therefore,
Mole fraction of KI = Moles of KI / Moles of KI+ Moles of Water
= 0.12 / 0.12+ 4.44
= 0.0263
∴ Mole fraction of KI = 0.0263
Intext Q 2.6 H2S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H2S in water at STP is 0.195 m, calculate Henry’s law constant
A 2.6 According to Henry's law,"At a constant temperature, the amount of a given gas that dissolves in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid."
Stated as,
p = KHx
Where, P = partial pressure of the solute above the solution
KH = Henry's constant
x = concentration of the solute in the solution
Given,
Solubility of H2S in water at STP is 0.195 m
We know,
At STP pressure p = 0.987 bar
0.195 mol of H2S is dissolved in 1000g of water
Moles of water = 1000/18
= 55.56 g/mol
∴ the mole fraction of H2S = Moles of H2S / Moles of H2S + Moles of water
= 0.195 / 0.195+55.6
= 0.0035
According to Henry's law, p = KHx
KH = p/x
KH = 0.987 / 0.0035
KH = 282 bar
∴ The Henry’s law constant is 282 bar
Intext Q 2.7 Henry’s law constant for CO2 in water is 1.67x10^8 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at 298 K.
A 2.7 According to Henry's law, "At a constant temperature, the amount of a given gas that dissolves in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid."
Stated as,
p = KHx
Where,
P = partial pressure of the solute above the solution
KH = Henry's constant
x = concentration of the solute in the solution
Given,
KH = 1.67x108 Pa
PCO2 2.5 atm = 2.5 × 1.01325 × 105Pa
According to Henry's law,
p = KHx
x = P/KH
x = 2.5 X 1.01325 X 105 / 1.67 X 108
x = 0.00152
In 500 ml of soda water there is 500 ml of water (neglecting soda)
Mole of water = 500/18
= 27.78 mol
Now,
x = nco2 / nco2 + nH2o
nco2 = x X nH2o
= 0.00152 X 27.78
= 0.042 mol
Hence, quantity of CO2 in 500mL of soda water 0.042 × 44 = 1.848 g
Intext Q 2.8 The vapour pressure of pure liquids A and B are 450 and 700 mm Hg respectively, at 350 K . Find out the composition of the liquid mixture if total vapour pressure is 600 mm Hg. Also find the composition of the vapour phase.
Given, PAo = 450 mm Hg
PBo = 700 mm Hg
ptotal = 600 mm of Hg
By using Rault's law,
ptotal = PA + PB
ptotal = PAoxA + PBoxB
ptotal = PAoxA + PBo( 1 - xA )
ptotal = (PAo- PBo)xA + PBo
600 = (450 - 700) xA + 700
-100 = -250 xA
xA = 0.4
∴ xB = 1 - xA
xB = 1 – 0.4
xB = 0.6
Now,
PA = PAoxA
PA = 450 × 0.4
PA = 180 mm of Hg and
PB = PBox
PB = 700 × 0.6
PB = 420 mm of Hg
Composition in vapour phase is calculated by
Mole fraction of liquid,
A =PA / PA + PB
= 180/180+420
= 0.30
Mole fraction of liquid,
B =PB / PA + PB
= 420 / 180+420
= 0.70
Intext Q 2.9 Vapour pressure of pure water at 298 K is 23.8 mm Hg. 50 g of urea (NH2CONH2 ) is dissolved in 850 g of water. Calculate the vapour pressure of water for this solution and its relative lowering.
A 2.9 Given,
Vapour pressure of water, PIo = 23.8 mm of Hg
Weight of water, w1 = 850 g
Weight of urea, w2 = 50 g
Molecular weight of water, M1 = 18 g/mol
Molecular weight of urea, M2 = 60 g/mol
n1 = w1/M1 = 850/18 = 47.22 mol
n2 = w2/M2 = 50/60 = 0.83 mol
We have to calculate vapour pressure of water in the solution p1
By using Raoult's therom,
PI = 23.4 mm of Hg Hence,
The vapour pressure of water in the solution is 23.4mm of Hg and its relative lowering is 0.0173.
Intext Q 2.10 Boiling point of water at 750 mm Hg is 99.63°C. How much sucrose is to be added to 500 g of water such that it boils at 100°C.
A 2.10 Given,
Mass of water, wl = 500 g
Boiling point of water = 99.63°C (at 750 mm Hg).
Molal elevation constant, Kb = 0.52 K kg/mol
Molar mass of sucrose (C12H22O11), M2 (11 × 12 + 22 × 1 + 11 × 16) = 342 g/mol
Elevation of boiling point ΔTb = (100 + 273) - (99.63 + 273) = 0.37 K
We know that,
ΔTb = Kb X 1000 X W2 / M2 X W1
0.37 = 0.52 X 1000 X W2 / 340 X 500
w2 = 0.37 X 342 X 500 / 0.52 X 1000
w2 = 121.67 g
Hence,
121.67 g (approx) Sucrose is added to 500g of water so that it boils at 100°C.
Intext Q 2.11 Calculate the mass of ascorbic acid (Vitamin C, C6H8O6 ) to be dissolved in 75 g of acetic acid to lower its melting point by 1.5°C. Kf = 3.9 K kg mol^-1.
A 2.11 Given
Mass of acetic acid, w1 = 75 g
Lowering of melting point, ΔTf = 1.5 K
Kf = 3.9 K kg/mol
Molar mass of ascorbic acid (C6H8O6), M2 6 × 12 + 8 × 1 + 6 × 16 = 176 g/mol[1]
We know that,
= 5.08 g
Hence,
5.08 g of ascorbic acid is needed to be dissolved.
Intext Q 2.12 Calculate the osmotic pressure in pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 185,000 in 450 mL of water at 37°C.
A 2.12 Given,
Volume of water, V = 450 mL = 0.45 L
Temperature, T=(37 + 273)K = 310 K
1.0 g of polymer of molar mass 185,000
Number of moles of polymer, n = 1 / 185,000 mol
We know that,
Osmotic pressure, π = nRT/V
= 1 X 8.314 X 103 X 310 / 185000 X 0.45
= 30.98 Pa
= 31 Pa (approx)
Exercise Q 2.1 Define the term solution. How many types of solutions are formed? Write briefly about each type with an example
A 2.1 A solution is a homogeneous mixture of two or more than two substances on molecular level whose composition can vary within certain limits.
The part or component of the mixture present in a lesser amount is called
the SOLUTE and the one present in larger amount is called the SOLVENT. For eg- small amount of salt [solute] dissolved in water [solvent].
There are nine types of solutions formed. They are:
|
Sr.No. |
State of solute |
State of solvent |
Examples |
|
1 |
GAS |
GAS |
Air |
|
2 |
GAS |
LIQUID |
Oxygen in water, carbonated water |
|
3 |
SOLID |
GAS |
Smoke particles in air, dust particles in air |
|
4 |
LIQUID |
GAS |
Mist |
|
5 |
LIQUID |
LIQUID |
Alcohol in water |
|
6 |
LIQUID |
SOLID |
Mercury in silver |
|
7 |
GAS |
SOLID |
Adsorption of hydrogen over palladium or platinum |
|
8 |
SOLID |
LIQUID |
Sugar in water |
|
9 |
SOLID |
SOLID |
Carbon in Iron(steel), Alloy |
Out of these nine types solution, solid in liquid, liquid in liquid & gas in liquid are very common. When the components of the solution are mixed, the resulting solution may exist in any of the three possible states of matter that is solid, liquid or gaseous.
They are:
- (1) Gaseous solution: In such solutions solvent is Since the solvent is gas,the solute can be solid, liquid or gas. For example, a mixture of oxygen and nitrogen gas is a gaseous solution.
- (2) Liquid solution: In such type of solutions liquid acts as the solvent. The solute in these solutions may be gas, liquid, or solid.
- (3) Solid solutions: As the name suggests, in such solutions solid acts as the solvent. The solute in these solutions may be a gas, liquid or solid. For example, a solution of copper in gold is a solid solution.
Exercise Q 2.2 Give an example of a solid solution in which the solute is a gas.
A 2.2 As the name signifies, a solid solution is one in which solvent is solid.So considering this aspect absorption of hydrogen over platinum or palladium is an example of such solution. Platinum or palladium is used as a catalyst in hydrogenation processes.
Exercise Q 2.3 Define the following terms: (i) Mole fraction (ii) Molality (iii) Molarity (iv) Mass percentage
A 2.3 (1) Mole fraction - The mole fraction of a particular component in a solution is the ratio of the number of moles of that component to the total number of moles of all the components present in the solution.
Mathematically,
Mole Fraction of component = Number of moles of given component / Total number of moles in solution
Mole Fraction is independent of temperature.
- (2) Molality - Molality of a solution is defined as the number of moles of solute dissolved per 1000g [1kg] of the It is represented by m.
Molality actually represents the concentration of solution in mol / kg.
Mathematically,
Molality = Number of moles of solute/ Mass of solvent in kg
It is represented by m.
- (3) Molarity- The number of moles of solute dissolved per litre of the solution at a particular temperature is called the molarity of the solution at that
Molarity actually represents the concentration of a solution in mol / L.
Mathematically,
Molarity = Number of moles of solute/ Volume of solution in litres
- (4) Mass percentage - Mass percentage is defined as the mass of the solute in grams dissolved per 100g of the It is also referred to as weight percentage [w/w].
For example, 10% [by mass] urea solution means that 10 g of urea are present in 100 g of solution, the solvent being only 100-10 = 90 g.
Mathematically, the mass percentage of a solute in a solution is given by:
Mass Percentage of Solute = Mass of solute / Mass of solute + Mass of solvent X 100
Or
Mass Percentage of Solute = Mass of solute / Mass of solution X 100
Exercise Q 2.4 Concentrated nitric acid used in laboratory work is 68% nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504 g mL^–1?
A 2.4 Given:
Concentration of Nitric Acid, HNO3 = 68%
Density of solution, d = 1.504 g/ml
To find: Molarity, Mo
Formula:
Density, d = Mass (M) / volume (V)
Molarity, Mo = Number of moles of solute/ Volume of solution in litres
Solution:
68% of Nitric acid by mass in aqueous solution means that 68g [[68 × 100]/100] of Nitric acid present in 100g of solution.
⇒ Molecular mass of Nitric Acid, HNO3 = [1 × 1] + [1 × 14] + [16 × 3]
= 63g
⇒ Number of moles of Nitric Acid = [68/63]
= 1.079 moles
⇒ Given Density, d = 1.504 g/ml
⇒ Volume, v = [100/1.504]
= 66.489 ml
⇒ Molarity, Mo = [1.079/66.489] × 1000
= 16.23 M
Therefore the molarity of the sample is 16.24 M.
Exercise Q 2.5 .A solution of glucose in water is labelled as 10% w/w, what would be the molality and mole fraction of each component in the solution? If the density of solution is 1.2 g mL^–1, then what shall be the molarity of the solution?
A 2.5 Given:
10% w/w solution means that if solution is of 100g then 10g of glucose is present in it [[10 × 100]/100] and the amount of water present in it is [100-10], Mw = 90g.
Density, d = 1.2g/ml
To find: Molality and Mole Fraction of Each component Formula:
Density, d = Mass (M) /volume (V)
Molality = Number of moles of solute/ Mass of solvent in kg
Mole Fraction of component = number of moles of given component / total number of moles in solution
Molarity, Mo = Number of moles of solute/ Volume of solution in litres
Solution:
Calculation of Molality:
⇒ Molecular mass of Glucose, [C6H12O6] = [6 × 12] + [12 × 1] + [6 × 16]
= 72 + 12 + 96
= 180g
⇒ Number of moles of Glucose, Ng = [10/180]
= 0.0556 moles
⇒ Molality = Ng/MW
⇒ Molality = 0.0556/ 0.09
= 0.6177 m
≈ 0.62 m
Calculation of Mole Fraction:
⇒ Molecular Mass of Water, [H2O] = [2 × 1] + [16 × 1]
= 2 + 16
= 18g
⇒ Number of moles of water, Nw = [90/18]
= 5 moles
⇒ Mole Fraction of Glucose,
xg = NG / NW + NG
= 0.0556 / 5+0.0556
= 0.011
⇒ Mole Fraction of Water, xw = (1-xg)
= 1 – 0.011
= 0.989
Calculation of Molarity:
From density we can find out volume.
⇒ Volume, V = [100/1.2]
= 83.33 ml
⇒ Molarity = 0.0556/ 83.33 X 1000
Molarity, M = 0.667 M
≈ 0.67 M
Therefore the answers obtained in the numerical can be summarized in following table:
| Quantity |
Answer |
| Molality, m |
0.62 m |
| Mole Fraction of Glucose |
0.011 |
| Mole Fraction of Water |
0.989 |
| Molarity, M |
0.67 M |
Exercise Q 2.6 How many mL of 0.1 M HCl are required to react completely with 1 g mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both?
A 2.6 Given:
Molarity of HCl, = 0.1 M
Mass of Mixture = 1g
To find: Volume of HCl to react completely with mixture
Formula:
Molarity, Mo = number of moles of solute/ Volume of solution in litres
Solution:
Calculation of Amount of each component in mixture:
⇒ Let the amount of Na2CO3 be X g
⇒ And Let amount of NaHCO3 be [1-X] g
⇒ Molecular Weight of Na2CO3 = [23 × 2] + [12] + [3 × 16]
= 106 g
⇒ Molecular Weight of NaHCO3 = [23] + [1] + [12] + [3 × 16]
= 84 g
⇒ Number of moles of NaHCO3 = 1-x / 84
⇒ Number of moles of Na2CO3 = x / 106
Now it is given in the question that the mixture is equimolar, so
⇒ Number moles of Na2CO3 = Number of moles of NaHCO3
1-x/84 = x/106
106 – 106X = 84X
190X = 106
x= 106/190
X = 0.5579
≈ 0.558
Amount of Na2CO3 = 0.558 g
⇒ Amount of NaHCO3 = 1- 0.558 g = 0.442 g
⇒ Number moles of Na2CO3 = [0.558/106]
= 0.00526 moles
⇒ Number of moles of NaHCO3 = 0.00526 moles …. [Mixture is equimolar]
Calculation of volume of HCl required
⇒ In the question it is given that HCl reacts with the mixture.
Na2CO3 + 2HCl → 2NaCl + H2O + CO2
NaHCO3 + HCl → NaCl + H2O + CO2
From the above chemical equations it can be found that 2 moles of HCl is required to react with one mole of Na2CO3 and 1 moles of HCl is required to react with one mole of NaHCO3.
So total number of moles of HCl required to completely react with mixture is as follows:
⇒ Total Number of Moles of HCl = [2 × 0.00526] + 0.00526
= 0.01578 moles
From Molarity Formula we have,
Molarity, Mo = number of moles of solute/ volume in litres (V)
⇒ Volume in litres, V = [0.01578/0.1]
= 0.1578 L
⇒ Volume in ml, V = 0.1578 × 1000
= 157.8 ml
Therefore the volume of 0.1 M HCl are required to react completely with 1 g mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both is 157.8 ml.
Exercise Q 2.7 A solution is obtained by mixing 300 g of 25% solution and 400 g of 40% solution by mass. Calculate the mass percentage of the resulting solution.
A 2.7 Let the first solution be solution A and second solution be solution B. Given:
⇒ Mass of Solute in solution A, Ma = [25 × 300]/100
= 75g
⇒ Mass of Solute in solution B, Mb = [40 × 400]/100
= 160g
To find: Mass Percentage of Solute
Formula:
Mass Percentage of Solute = mass of solute/ mass of solution X 100
Solution:
⇒ Total mass of Solute in mixture, M = Ma + Mb
= [75 + 160]
= 235g
⇒ Total mass of solution = 300 + 400
= 700g
⇒ Mass Percentage of Solute = 235/700 X 100
= 33.5%
⇒ Percentage of Water in final solution = 100-33.5
= 66.5%
Therefore mass percentage of solute is 33.5% and that of water is 66.5%.
Exercise Q 2.8 An antifreeze solution is prepared from 222.6 g of ethylene glycol (C2H6O2 ) and 200 g of water. Calculate the molality of the solution. If the density of the solution is 1.072 g mL^–1, then what shall be the molarity of the solution?
A 2.8 Given:
Mass of ethylene glycol (C2H6O2) = 222.6 g
Mass of water = 200 g
Density, d = 1.072 g/ml
To find: Molality and Molarity of solution
Formula:
Molality = Number of moles of solute/ Mass of solvent in kg
Molarity, Mo = number of moles of solute/ volume of solution in litres
Density, d = Mass (M) / volume (V)
Calculation of Molality:
⇒ Molecular Mass of ethylene glycol (C2H6O2) = [12 × 2] + [6 × 1] + [16 × 2]
= 24 + 6 + 32
= 62 g
⇒ Number of moles of ethylene glycol (C2H6O2) = [222.6/62]
= 3.59 moles
⇒ Mass of water = 200 g
⇒ Molality = numebr of moles of solute/ Mass of solvent in kg
= 3.59 / 200 X 1000
= 17.95 m
Calculation of Molarity:
⇒ Total mass of solution = [222.6 + 200]
= 422.6 g
From density formula we can find out the volume required.
⇒ Volume of solution, V = [422.6 /1.072]
= 394.216 ml
⇒ Molarity, Mo = number of moles of solute/ volume of solution in litres
⇒ Molarity, Mo =3.59 / 394.216 X 1000
⇒ Molarity = 9.1067
⇒ Molarity ≈ 9.11 M
Therefore the Molality and Molarity of the solution is as follows:
Molality = 17.95 m
Molarity = 9.11 M
Exercise Q 2.9 A sample of drinking water was found to be severely contaminated with chloroform (CHCl3 ) supposed to be a carcinogen. The level of contamination was 15 ppm (by mass): (i) express this in percent by mass (ii) determine the molality of chloroform in the water sample.
A 2.9 Given:
Level of contamination = 15 ppm [by mass]
To find: Mass Percentage and Molality
Formula:
Molality = Number of moles of solute / Mass of solvent in kg
Mass Percentage of Solute = Mass of solute / Mass of solution X 100
Solution:
Calculation of Mass Percentage:
15 ppm means 15 parts of Chloroform in 106 parts of drinking water
⇒ Mass Percentage = Mass of choloroform / Total mass X 100
= 15 / 106 X 100
= 1.5 × 10-3
Calculation of Molality:
⇒ Molecular Mass of Chloroform, CHCl3 = [12] + [1] + [35.5 × 3]
= 119.5 g
⇒ Number of Moles of Chloroform = [15 / 119.5]
= 0.1255 moles
Molality = Number of moles of solute / Mass of solvent in kg
= 0.1255 / 106 X 1000
= 1.255 × 10-4
Therefore the Mass Percentage is = 1.5 × 10-3 and the Molality of the solution is = 1.255 × 10-4 m.
Exercise Q 2.10 What role does the molecular interaction play in a solution of alcohol and water?
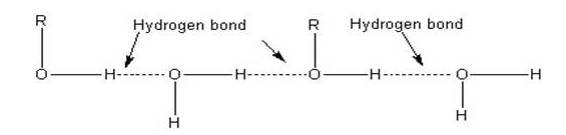
A 2.10 The lower members of alcohols are completely miscible [highly soluble] with water but the solubility decreases with increase in the molecular weight. The lower members of the alcohol group have the capability to form intermolecular hydrogen bonding with water molecules as alcohols are polar molecules in nature.
Alkyl groups are hydrophobic [prevents formation of hydrogen bonds with water] in nature. In lower alcohols, the alkyl group is small and the –OH group of alcohol is effective in making hydrogen bonds with water.
But with the increase in the size of alkyl group, the hydrophobic [water hating] nature of alkyl group dominates over the hydrophilic [water liking] nature of –OH group making the molecule less soluble in water. So solubility of alcohols decreases with increase in its molecular mass.
Since molecular interaction is weaker between higher alcohols and water, as a result, when alcohol and water are mixed, the intermolecular interactions become weaker and the molecules can easily get liberated off. This increases the vapour pressure of the solution, which in turn lowers the boiling point of the resulting solution.
Exercise Q 2.11 Why do gases always tend to be less soluble in liquids as the temperature is raised?
A 2.11 Whenever a gas is dissolved in a liquid, a small amount heat is liberated in the process. So dissolving a gas in liquid is overall an exothermic process.
So according to the LeChatelier principle, whenever the temperature is increased for a reaction which is exothermic in nature, the equilibrium shifts backwards and the reaction proceeds in backward direction that means the solution gets dissociated and will give off gas and hence solubility of gas decreases.
So with the increase in temperature, the solubility of the gases in liquids decreases.
Exercise Q 2.12 State Henry’s law and mention some important applications.
A 2.12 The solubility of a gas in water depends on following three parameters:
- Nature of gas
- Temperature
- Pressure
The solubility decreases with increase in temperature. Temperature and pressure follow inverse proportionality. So solubility increases with increase with pressure. A quantitative relation between pressure and solubility of a gas in a solvent was given by W. Henry [1803]. This relationship is known as Henry’s law.
Statement:
Henry’s law can be expressed as follows.
At constant temperature, the solubility of a gas in a liquid is directly proportional to the pressure of the gas.
Mathematically,
Solubility ? Pressure of the gas
Some of the important applications of Henry’s law are as follows.
- (i) Since the solubility of a gas in water increases with pressure, soft drink bottles are sealed under high pressure to accommodate more CO2 in the soft drink making the drink fizzier.
- (ii) If deep sea divers [scuba divers] use air for respiration, they develop a medical condition known as bends with involves the blocking of capillaries. This is because air is mainly a mixture of oxygen and According to Henry’s Law, the solubility of gases increases with increase in pressure. When diver breathes air under high pressure in water, nitrogen dissolves in his blood. When the diver comes towards surface, the pressure gradually decreases. This releases the dissolved gases and leads to the formation of bubbles in the blood. This is quite painful and dangerous to life. In order to avoid bends and toxic effects of dissolved nitrogen in blood, the tanks used by sea divers are filled with air diluted with helium [ 11.7% He + 56.2% N2 + 32.1% O2 ].
- (iii) The pressure of oxygen in air decreases in going up the mountains. At very high altitudes the partial pressure of oxygen in air is much less than that at the ground Therefore, people living at high altitude or climbers have low concentrations of oxygen in the blood and tissues. This leads to weakness and loss in the clarity of thinking. These symptoms create a condition known as anoxia.
- (iv) Henry’s law is also related to biology as it explains the supply of inhaled oxygen to tissues. When air is inhaled, it combines with haemoglobin [oxygen carrier of RBCs] of the blood in lungs to form oxyhaemoglobin because in lungs the partial pressure of oxygen is high. Partial pressure of oxygen is low in tissues. Hence, oxygen is released from oxyhaemoglobin and is utilised by the cells to carry out their tasks.
Exercise Q 2.13 The partial pressure of ethane over a solution containing 6.56 × 10^–3 g of ethane is 1 bar. If the solution contains 5.00 × 10^–2 g of ethane, then what shall be the partial pressure of the gas?
A 2.13 Given:
Mass of ethane in solution A = 6.56 × 10–3 g
Partial pressure of solution A = 1 bar
Mass of ethane in solution B = 5.00 × 10–2 g
To find: Partial Pressure of gas
Formula:
By Henry’s law:
Mass of dissolved gas M = k × P Where
k = proportionality constant
P = Partial Pressure
Solution:
⇒ M1 = k × P1................. [1]
⇒ M2 = k × P2................. [2]
Dividing the [2] by [1], we get
M2/M1 = P2/P1
P2 = M2 X P1 / M1
P2 = 5 X 10–2 X 1 / 6.56 X 10–3
P2 = 7.62 bar
Therefore the partial pressure of the gas is 7.62 bar.
Exercise Q 2.14 What is meant by positive and negative deviations from Raoult's law and how is the sign of ∆mixH related to positive and negative deviations from Raoult's law?
A 2.14 Raoult’s law states that at a given temperature, the vapour pressure of a solution containing non volatile solute is directly proportional the mole fraction of the solvent.
Non ideal solutions show positive and negative deviations from ideal behaviour.
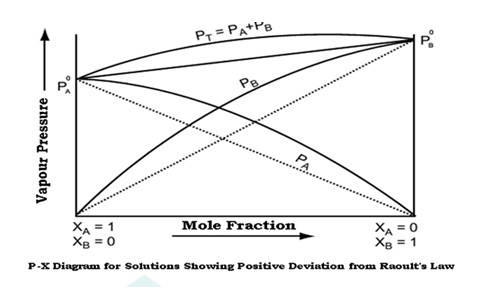
Non ideal solutions showing positive deviations from Raoult’s law-
A solution is said to show positive deviation from Raoult’s Law when at any composition, its vapour pressure is higher than that given by Raoult’s Law.
The positive deviation is shown by those liquid pairs in which the A-B molecular interaction forces are weaker than the corresponding A-A or B-B molecular interaction forces. When the A-B molecular interaction forces are weaker, then molecules of liquid A find it easier to escape as compared to pure solution thereby increasing the vapour pressure of solution.
As a result, each component of solution has a partial vapour pressure greater than expected on the basis of Raoult’s law. This is called positive deviations from Raoult’s law, that is PA>PAoXA and PB>PBoXB
∆mixH [Change in Enthalpy] is positive because energy is required to break A-A & B-B attractive forces. Hence it is an endothermic process.
Examples of liquid Pairs:
- Water + methanol
- Water + ethanol
- Acetone + benzene
- Carbon tetrachloride + benzene
The graph of vapour pressure and mole fraction for liquids showing positive deviation from Raoult’s Law is shown below:
From the diagram it is clear that the composition curve of such a solution lies above the composition curve obtained on basis of Raoult’s Law
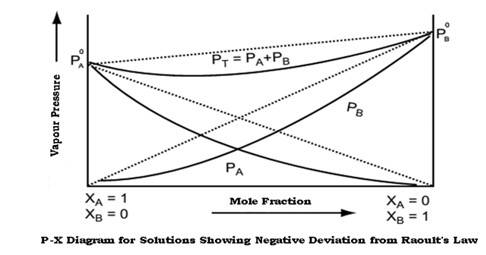
Non ideal solutions showing Negative deviations from Raoult’s law –
When the vapour pressure of the solution is lower than that calculated on the basis of Raoult’s Law, the solution is said to show negative deviation from Raoult’s Law. Even the vapour pressure of individual components show negative deviation from Raoult’s Law
The negative deviation is shown by those liquid pairs in which the A-B molecular interaction forces are stronger than the corresponding A-A or B-B molecular interaction forces. When the A-B molecular interaction forces are stronger, then molecules of liquid A find it easier to escape from pure solution as compared to the mixture thereby decreasing the vapour pressure of solution.
Consequently, each component of solution has a partial vapour pressure less than expected on the basis of Raoult’s law. This is called negative deviations from Raoult’s law, i.e. PA
Examples of liquid pairs:
- Water + hydrochloric acid
- Water + nitric acid
- Chloroform + benzene
- Acetone + aniline
∆mixH is negative because energy is released due to increase in attractive forces. Hence it is an exothermic process.
The graph of vapour pressure and mole fraction for liquids showing negative deviation from Raoult’s Law is shown below:
Exercise Q 2.15 An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
A 2.15 given:
2% non-volatile solute in an aqueous solution means that if the solution is of mass 100 g then the mass of solute in the solution is,
Mass of solute = [2 × 100]/100
= 2 g
∴ Mass of Solvent = 100-2
= 98 g
Vapour pressure of solution at normal boiling point, P1 = 1.004 bar
Vapour pressure of pure water at normal boiling point, P1° = 1 atm = 1.013 bar
To find: Molar mass of solute
Formula:
From Raoult’s Law, we have:
Now we know that number of moles of solute is given by the following relationship,
⇒ Number of moles = Mass of solute / Molecular mass of solute
Using the above relationship the equation [1] can be modified as follows:
Where
W1 = mass of solvent
W2 = mass of solute
M1 = molecular mass of solvent
M2 = molecular mass of solute
Solution:
(1.013 - 1.004) / 1.013 = 2 X 18 / 98 X M2
0.009 / 1.013 = 36 / 98M2
M2 = 36 X 1.013 / 98 X 0.009
M2 = 41.3469 g
∴ M2 ≈ 41.35 g
Therefore the molar mass of the solute is 41.35 g.
Exercise Q 2.16 Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure of a mixture of 26.0 g of heptane and 35 g of octane?
A 2.16 Given: Temperature = 373k
Vapour pressure of pure heptane (p10 ) = 105.2 kpa and that of octane (p20 ) = 46.8 kpa
Mass of heptane = 26 g
Mass of octane = 35 g
Molecular weight of heptane = C7H16 = 12 × 7 + 1 × 16 = 100 gmol-1
Molecular weight of octane = C8H18 = 114 gmol-1
Moles of heptane, n1 = given mass /molecular weight = 26/100
⇒ n1 = 0.26mol
Moles of octane, n2 = given mass /molecular weight = 35/114
⇒ n2 = 0.307mol
∴ Partial pressure of heptane, p1 = χ1 × p10
⇒ p1 = 0.456 × 105.2 = 47.97kpa
∴ Partial pressure of octane, p1 = χ2 × p20
⇒ p2 = 0.544 × 46.8 = 25.46 kpa
∴ Total pressure exerted by solution = p1 + p2
= 47.97 + 25.46
= 73.43 kpa
Exercise Q 2.17 The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
A 2.17 Given: 1 molal solution means 1 mole of solute present in 1000g of water solvent)
Molecular weight of water = H2O = 1 × 2 + 16 = 18g/mol
No. of moles of water, n = given mass /molecular weight
⇒ n = 1000/18 = 55.56 gmol-1
Mole fraction of solute in solution,x2 = moles of solute/(moles of solute + moles of water)
⇒ x2 = 1/(1 + 55.56)
⇒ x2 = 0.0177
Given vapour pressure of pure water at 300k is 12.3 kpa
Apply the formula:
⇒ P1 = 12.0823kpa
which is the vapour pressure of the solution.
Exercise Q 2.18 Calculate the mass of a non-volatile solute (molar mass 40 g mol^–1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
A 2.18 Given:
Molar mass of non-volatile solute = 40g
Let no. of moles of solute be n.
Mass of octane = 114g
Molar mass of octane(C8H18) = 12 × 8 + 1 × 18 = 114g/mol
Moles of octane = given mass/molar mass
⇒ n = 114/114 moles
⇒ n = 1 mole
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
⇒ x2 = n/n + 1
Let the vapour pressure of original solvent(without solute) be p1⁰
Accordingly after addition of solute vapour pressure of solution reduces to 80% i.e.
0.8 p1⁰ = p1
Applying the formula:
⇒ n/n + 1 = 0.2
⇒ 0.2n + 0.2 = n
⇒ n = 0.25 moles
Hence, mass of solute is:
moles = given mass/molar mass
⇒ 0.25moles = mass/40g
⇒ mass = 10g.
Exercise Q 2.19 A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further, 18 g of water is then added to the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate: (i) molar mass of the solute (ii) vapour pressure of water at 298 K.
A 2.19 Given: mass of solute = 30g
Let the molar mass of solute be x g and vapour pressure of pure water at 298k be P1 ⁰
Mass of water(solvent) = 90g
Molar mass of water = H2O = 1 × 2 + 16 = 18g
Moles of water = mass of water/molar mass
⇒ n = 90/18 moles
⇒ n = 5moles
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
x2 = (30/x) / (30/x) + 5
x2 = 30 / 30+5x
Vapour pressure of solution (p1) = 2.8kpa
Applying the formula:
According to second condition when we add 18g of water to solution vapour pressure becomes 2.9kpa
Moles of water = mass/molar mass
⇒ n = 90 + 18/18
⇒ n = 6moles
Molar fraction of solute,
x2 = moles of solute / moles of solute + moles of octane
x2 = (30/x) / (30/x) + 6
x2 = 30 / 30+6x
Applying the formula:
Solving 1 and 2:
Dividing (2) by (1) we get
(i) molar mass of the solute = 78g
(ii) vapour pressure of water at 298 K = 537kpa
Exercise Q 2.20 A 5% solution (by mass) of cane sugar in water has freezing point of 271K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.
A 2.20 5% solution means 5g of cane sugar is present in 100g of solution
Freezing point of solution = 271k
Freezing point of pure water = 273.15k
Molar mass of cane sugar(C12H22O11) = 12 × 12 + 1 × 22 + 16 × 11 = 342g
Moles of cane sugar = mass/molar mass = 5/342
⇒ n = 0.0146mol
Molality of solution = moles of solute/mass of solvent(in kg)
⇒ M = 0.0146/0.095
⇒ Molality = 0.154M
Depression in freezing point = ΔTf = 273.15-271 = 2.15k
Applying the formula: ΔTf = Kf × M
Where
ΔTf = depression in freezing point
Kf = molal depression constant
M = molality of solution
⇒ Kf = 2.15/0.154
⇒ Kf = 13.96k kg mol-1
Second condition: mass of glucose = 5g
Molar mass of glucose(C6H12O6) = 12 × 6 + 1 × 12 + 16 × 6 = 180g
Moles of glucose = mass/molar mass
⇒ n = 5/180moles
⇒ n = 0.0278mol
Molality of solution = moles of solute/mass of solvent(in kg)
⇒ molality = 0.0278/0.095
⇒ M = 0.2926M
Applying the formula: ΔTf = Kf × M
Where
ΔTf = depression in freezing point
Kf = molal depression constant
M = molality of solution
⇒ ΔTf = 13.96 × 0.2926
⇒ ΔTf = 4.08k
Freezing point of solution = 273.15 + 4.08 = 277.234k
Exercise Q 2.21 Two elements A and B form compounds having formula AB2 and AB4 . When dissolved in 20 g of benzene (C6H6 ), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol^–1. Calculate atomic masses of A and B
A 2.21 let the molar masses of AB2 and AB4 be x and y respectively.
Molar mass of benzene(C6H6) = 12 × 6 + 1 × 6 = 78 g/mol
Moles of benzene = mass/molar mass = 20/78
n = 0.256mol
⇒ ΔTf = 2.3 K
Kf = 5.1K kg mol-1
For AB2
Applying the formula: ΔTf = Kf × M
Where
ΔTf = depression in freezing point
Kf = molal depression constant
M = molality of solution
⇒ 2.3 = 5.1 × M1
⇒ M1 = 0.451mol/kg
For AB4
Applying the formula: ΔTf = Kf × M
ΔTf = depression in freezing point
Kf = molal depression constant
M = molality of solution
⇒ 1.3 = 5.1 × M2
⇒ M2 = 0.255mol/kg
M1 = moles of solute/mass of solvent(in kg)
M1 = 1/x / 0.02 = 1 / 0.02x = 0.451
⇒ X = 110.86g
M2 = moles of solute/mass of solvent(in kg)
M2 = 1/y / 0.02 = 1 / 0.02y = 0.255
⇒ y = 196.1g
atomic mass of A be a and that of B be b g respectively.
So, AB2 : a + 2b = 110.86
AB4: a + 4b = 196.1
⇒ a = 25.59g
⇒ b = 42.64g
Exercise Q 2.22 At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?
A 2.22 Here,
T = 300 K
π = 1.52 bar
R = 0.083 bar L
Applying the relation, π = CRT
where
π = osmotic pressure of solution
C = concentration of solution
R = universal gas constant
T = temperature
⇒C = π / RT = 1.52 / 0.083 X 300
⇒ C = 0.061mol/L
Concentration of the solution is 0.061mol/L
Exercise Q 2.23 Suggest the most important type of intermolecular attractive interaction in the following pairs. (i) n-hexane and n-octane (ii) I2 and CCl4 (iii) NaClO4 and water (iv) methanol and acetone (v) acetonitrile (CH3CN) and acetone (C3H6O)
- A 2.23 (i) Both the compounds are non-polar and they do not attract each other because they do not form any polar ions. Vanderwaals forces of attraction will be dominant in between them as vanderwaals forces of attraction are not a result of any chemical or electronic bond.
- (ii) now here both the compounds are non-polar because in I2 both the atoms are same so they have same electronegativity and hence there will be no displacement of electron cloud, it will be in the centre. In case of CCl4 molecule, it has tetrahedral shape so two Cl atoms will cancel the attraction effect from two opposite Cl atoms, hence molecule as a whole is non polar. Therefore they will also have vanderwaals forces of attraction.
- (iii) NaClO4 is ionic in nature as Na, Cl and O all have different electronegativity and their shape is also not symmetric. So molecular will be ionic in nature and we know that water is polar because O will attract the electron cloud towards it(more electronegative) hence there will be formation of dipole(two oppositely charged ions separated by a short distance). Therefore there will be ion-dipole interaction between them.
- (iv) methanol and acetone are both polar molecules because of the presence of electron withdrawing O atom in methanol and ketone group in acetone. So they will have dipole-dipole interaction.
- (v) acetonitrile is polar compound due to presence of electronegative N atom and acetone due to ketone group. So, dipole-dipole interaction.
Exercise Q 2.24 Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain. Cyclohexane, KCl, CH3OH, CH3CN.
A 2.24 Now n-octane is non-polar solvent due to long chain saturated structure. We know that “like dissolves like” so a non-polar compound will be more soluble in non-polar solvent as compared to polar compound.
So cyclohexane is non-polar due to symmetric structure. KCl is ionic in nature as it will dissociate into K + and Cl- ions. CH3CN is polar as mentioned above and CH3OH is also polar in nature.
The order of increasing polarity is:
Cyclohexane < CH3CN < CH3OH < KCl (O is more electronegative than N)
Therefore, the order of increasing solubility is:
KCl < CH3OH < CH3CN < Cyclohexane
Exercise Q 2.25 Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water? (i) phenol (ii) toluene (iii) formic acid (iv) ethylene glycol (v) chloroform (vi) pentanol.
- A 2.25 Water is a polar compound (due to electronegativity difference between O and H) . We know that “like dissolves like”. So, a non-polar compound will be more soluble in non-polar solvent as compared to polar compound.
- Phenol has the polar group -OH and non-polar group –C6H5 and it can not form H bonding with water(presence of bulky non-polar group) . Thus, phenol is partially soluble in water
- Toluene has no polar Thus, toluene is insoluble in water.
- Formic acid (HCOOH) has the polar group -OH and can form H-bond with water. Thus, formic acid is highly soluble in water
- Ethylene glycol(OH-CH2-CH2-OH) has polar -OH group and can form H-bond with Thus, it is highly soluble in water.
- Chloroform is partly soluble as CHCl3 is polar in nature due to high electronegativity of Cl atoms, there will be production of partial + charge on H atom so it can form H bonding with water but it is also surrounded by 3 Cl atoms, so partly soluble
- Pentanol(C5H11OH) has polar -OH group, but it also contains a very bulky non- polar group –C5H11. Thus, pentanol is partially soluble in water
Exercise Q 2.26 If the density of some lake water is 1.25g mL^–1 and contains 92 g of Na+ ions per kg of water, calculate the molarity of Na+ ions in the lake.
A 2.26 Mass of ions = 92g
Molar mass of ions = Na+ = 23g(neglect the mass lost due to absence of a electron)
Moles of ions = mass of ions/molar mass
⇒ n = 92/23 moles
⇒ n = 4moles
Molality of solution = moles of solute/mass of solvent(in kg) Molality = 4/1 = 4M
Exercise Q 2.27 If the solubility product of CuS is 6 × 10^–16, calculate the maximum molarity of CuS in aqueous solution?
A 2.27 The Solubility product of CuS (ksp) = 6 × 10-16
CuS → Cu ++ + S2-
Let the s be solubility of CuS in mol/L
Ksp = [ Cu ++ ][S2]
Ksp = solubility product
6 × 10-16 = s × s = s2
⇒ S = 2.45 × 10-8 mol/L
Hence, the maximum molarity of CuS in an aqueous solution is 2.45 × 10-8 mol/L
Exercise Q 2.28 Calculate the mass percentage of aspirin (C9H8O4 ) in acetonitrile (CH3CN) when 6.5 g of C9H8O4 is dissolved in 450 g of CH3CN.
A 2.28 Total mass of solution = 6.5g + 450g = 456.5g
Therefore mass percentage of aspirin in solution = (mass of aspirine/total mass of solution) = 6.5/456.5
⇒ mass % of aspirine = 1.424%
Exercise Q 2.29 Nalorphene (C19H21NO3 ), similar to morphine, is used to combat withdrawal symptoms in narcotic users. Dose of nalorphene generally given is 1.5 mg. Calculate the mass of 1.5 × 10^–3 m aqueous solution required for the above dose.
A 2.29 molar mass of Nalorphene = 311g/mol
Now 1000g of solution contains 1.5 × 10-3 moles of Nalorphene(Molality of solution = moles of solute/mass of solvent (in kg)
⇒ 1.5 × 10-3 moles of Nalorphene = 1.5 × 10-3 × 311 = 0.4665g of Nalorphene
Therefore, total mass of the solution = (1000 + 0.4665) g
⇒ total mass = 1000.4665 g
This implies that the mass of the solution containing 0.4665 g of nalorphene is 1000.4665 g.
Therefore, mass of the solution containing 1.5 mg of nalorphene is:
Mass = 1000.4665 X 1.5 X 10-3 / 4.665 g
⇒ mass of solution containing required ions = 3.22 g
Hence, the mass of aqueous solution required is 3.22 g.
Exercise Q 2.30 Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 mL of 0.15 M solution in methanol.
A 2.30 Volume of the solution = 250mL = 0.25L
Let the no. of moles of solute be n
Molarity = No. of moles of solute/volume of solution
⇒ 0.15 = n/0.25
⇒ n = 0.0375moles
Molar mass of C6H5OH = 6×12 + 5×1 + 16 + 1 = 94g
Moles = mass/molar mass
⇒ 0.0375 = m/94
Mass of benzoic acid required = 3.525g.
Exercise Q 2.31 The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.
A 2.31 The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the pattern,
Acetic acid< trichloroacetic acid< trifluoroacetic acid.
This is because fluorine is more electronegative than chlorine. So, trifluoracetic acid is a stronger acid in comparison to trichloroacetic acid and acetic acid. And also, acetic acid is the weakest of all.
Explanation: Stronger acid produces more number of ions, therefore it has more ΔTf(depression in freezing point), hence lower freezing point. As the acidic strength increases, the acid gets more and more ionised.
Trifluoracetic acid ionizes to the largest extent. Hence, in this case, trifluoracetic acid being the strongest acid produces more number of ions(extent of ionisation and concentration of ions are more), high ΔTf(depression in freezing point)and lower freezing point and vice versa.
Exercise Q 2.32 Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10^–3 , Kf = 1.86 K kg mol^–1 .
A 2.32 Mass of CH3CH2CHClCOOH = 10 g
Mass of water = 250g
Ka = 1.4 × 10–3,
Kf = 1.86 K kg mol–1
Molar mass of CH3CH2CHClCOOH = 12 + 3 + 12 + 2 + 12 + 1 + 35.5 + 2 + 16 + 16 + 1
= 122.5 g mol–1
Number of moles of solute = Mass of Solute / Molar Mass
→ No. of moles = 10g / 122.5 g/mol
∴ No. of moles = 8.6 X 10–2 mol
Now, Molality is given as,
M = Number of moles of solute / kg of solvent
M= 8.6 X 10–2 X 1000 g/mol / 250 g
M = 0.3264 kg/mol
CH3CH2CHClCOOH = CH3CH2CHClCOO- + H +
| Initial moles |
1 |
0 |
0 |
|
Equilibrium moles |
(1-α) |
α |
α |
Total moles at equilibrium = (1-α) + 2 α
= 1 + α
In order to find out the depression in freezing point,
values of i(vant Hoff’s factor) and α(degree of dissociation) are to be found out.
To find out degree of dissociation, α
Exercise Q 2.33 19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.00 C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.
A 2.33 Given- w1 = 500g
W2 = 19.5g
Kf = 1.86 K kg mol-1
Molar mass of CH2FCOOH = 12 + 2 + 19 + 12 + 16 + 16 + 1
= 78 g mol-1
The depression in freezing point is calculated by,
→ (where, m is the molality)
= 1.86 X 19.5 / 78 X 1000/500
= 1.86 X 19.5 / 78 X 2
=0.93
∴ Δtf (calculated) = 0.93
To find out the vant Hoff’s factor, we use the formula,
i = observed Δtf / calculated Δtf
i = 1.0 (given) / 0.93
∴ i= 1.07
CH2FCOOH → CH2FCOO- + H +
To find out the degree of dissociation α, we use
Thus, the vant Hoff’s factor is 1.07 an the dissociation constant is 2.634x10-3
Exercise Q 2.34 Vapour pressure of water at 293 K is 17.535 mm Hg. Calculate the vapour pressure of water at 293 K when 25 g of glucose is dissolved in 450 g of water.
A 2.34 Given- Vapour pressure of water,
PA0 = 17.535 mm Hg
WB= 25 g of glucose
WA = 450g of water
Molar mass of water, H2O = 1 + 1 + 16 = 18 g mol-1
Molar mass of glucose, C6H12O6 = (12×6) + (1×12) + (16×6) = 180 g mol-1
Using Raoult’s law for solution of non-volatile solute,
PA0 - PA / PA0 = xB→ Equation 1
where xB is the mole fraction of the solute
xB = WB/MB X MB/WB
=25/180 X 18 / 450
xB = 1/180
Substituting the value of xB in equation 1, we get,
Thus, the vapour pressure of water at 293 K at the given conditions is 17.437 mm Hg
Exercise Q 2.35 Henry’s law constant for the molality of methane in benzene at 298 K is 4.27 × 10^5 mm Hg. Calculate the solubility of methane in benzene at 298 K under 760 mm Hg.
A 2.35 Given-
Henry’s law constant KH = 4.27X 105 mm Hg,
p = 760mm Hg,
Using Henry’s law,
Using the formula of lowering vapour pressure,
Thus, the solubility of methane in benzene is 0.023 moles
Exercise Q 2.36 100 g of liquid A (molar mass 140 g mol^–1) was dissolved in 1000 g of liquid B (molar mass 180 g mol^–1). The vapour pressure of pure liquid B was found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 Torr.
A 2.36 Given-
Mass of liquid A, WA = 100g, Molar mass, MA = 140 g mol-1
Mass of liquid B, WB = 1000 g, Molar mass, MB = 180 g mol-1
Using the formula below calculate the no. of moles in liquid A and B.
Number of moles = Mass / Molar Mass
Number of moles of liquid A, MA = 100/140 = 0.714 mol-1
Number of moles of liquid B, MB = 1000/ 180 = 5.556 mol-1
Using the formula,
mole fraction of a liquid = No. of moles of the liquid / total no of moles
we calculate the mole fraction of liquids A and B.
→ Mole fraction of A,
xA = 0.714 / (0.714 + 5.556)
∴ xA = 0.114
→ Mole fraction of B,
xB = 1- xA = 1 - 0.114
∴ xB = 0.886
Vapour pressure of pure liquid B, Po = 500 torr (given)
According to Henry`s law,
Thus, the vapour pressure of pure liquid A = 280.7 torr and
vapour pressure of liquid A in the solution = 32 torr
Exercise Q 2.37 Vapour pressures of pure acetone and chloroform at 328 K are 741.8 mm Hg and 632.8 mm Hg respectively. Assuming that they form ideal solution over the entire range of composition, plot ptotal, pchloroform, and pacetone as a function of xacetone. The experimental data observed for different compositions of mixture is: Plot this data also on the same graph paper. Indicate whether it has positive deviation or negative deviation from the ideal solution.
| 100 xacetone |
0 |
3.4.8 |
23.4 |
36.0 |
50.8 |
58.2 |
64.5 |
72.1 |
| pacetone /mm Hg |
0 |
54.9 |
110.1 |
202.4 |
322.7 |
405.9 |
454.1 |
521.1 |
| pchloroform /mm Hg |
632.8 |
548.1 |
469.4 |
359.7 |
257.7 |
193.6 |
161.2 |
120.7 |
A 2.37 The Ptotal for the values given in the graph is found out and plotted in the graph.
| ptotal(mm Hg) |
632.8 |
603.0 |
579.5 |
562.1 |
580.4 |
599.5 |
615.3 |
641.8 |
It can be observed from the graph that the plot for the p total of the solution curves downwards. Therefore, the solution shows negative deviation from the ideal behaviour.
Exercise Q 2.38 Benzene and toluene form ideal solution over the entire range of composition. The vapour pressure of pure benzene and toluene at 300 K are 50.71 mm Hg and 32.06 mm Hg respectively. Calculate the mole fraction of benzene in vapour phase if 80 g of benzene is mixed with 100 g of toluene.
A 2.38 Given-
Thus, mole fraction of benzene in vapour phase is 0.6744
Exercise Q 2.39 The air is a mixture of a number of gases. The major components are oxygen and nitrogen with approximate proportion of 20% is to 79% by volume at 298 K. The water is in equilibrium with air at a pressure of 10 atm. At 298 K if the Henry’s law constants for oxygen and nitrogen at 298 K are 3.30 × 10^7 mm and 6.51 × 10^7 mm respectively, calculate the composition of these gases in water.
A 2.39 Given-
KH for O2 = 3.30 × 107 mm Hg,
KH for N2 = 6.51 × 107 mm Hg
Percentage of oxygen (O2) = 20 %
Percentage of nitrogen (N2) = 79%
Total pressure = 10 atm
Using Henry’s law,
where, p is the partial pressure of gas in the solution and KH is Henry’s constant.
Exercise Q 2.40 Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27° C.
A 2.40 Given-
Vant Hoff’s factor, i = 2.47
osmotic pressure, π = 0.75 atm
Volume of solution = 2.5L.
To determine the amount of CaCl2, we use vant Hoff’s equation for dilute solutions, given as,
πV = inRT
where, n is the number of moles of solute, R is solution constant which is equal to the gas constant and T is the absolute temperature.
Hence, the amount of CaCl2 dissolved is 3.425g
Exercise Q 2.41 Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 litre of water at 25° C, assuming that it is completely dissociated.
A 2.41 Given-
Mass of K2SO4, w = 25 mg = 25 X 10-3 g,
Molar mass of K2SO4 = (39×2) + (32×1) + (16×4) = 174 g mol-1
Volume V = 2 liter
T = 250C + 273 = 298 K (add 273 to convert in Kelvin)
The reaction of dissociation of K2SO4 is written as,
K2SO4 → 2K + + SO42-
Number if ions produced = 2 + 1 = 3, hence vant Hoff’s factor, i = 3
Here, we use vant Hoff’s equation for dilute solutions, given as,
πV = inRT
where, n is the number of moles of solute, R is solution constant which is equal to the gas constant(0.082) and T is the absolute temperature (298 K).
Hence, the osmotic pressure of a solution is 5.27x10-3atm
Chemistry Ncert Solutions Class 12th Exam