NCERT Solutions for Class 11 Physics Chapter 4 Motion in A Plane: Topic-wise Questions & Answers PDF

Section Name	Topic Name
3.1	Introduction to Motion in a Plane
3.2	Scalars and vectors
3.3	Multiplication of vectors by real numbers
3.4	Addition and subtraction of vectors — graphical method
3.5	Resolution of vectors
3.6	Vector addition — analytical method
3.7	Motion in a plane
3.8	Motion in a plane with constant acceleration
3.9	Projectile motion
3.10	Uniform circular motion

 

Motion in a Plane covers numerical problems from topics such as scalars, vectors, projectile motion, uniform circular motion etc. The students can find the NCERT Class 11 Chapter 4 Motion in a Plane pdf solution here. The Class 11 Physics Chapter 4 PDF can be downloaded and referred later by the students.

Download Here: NCERT Solution for Class XI Physics Chapter Motion in a Plane PDF

Q.4.1 State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.

Ans.4.1

A scalar quantity depends only on the magnitude – volume, mass, speeds, density, number of moles, angular frequency are all scalar quantities.

A vector quantity depends on magnitude and direction – velocity, acceleration, displacement and angular velocity are all vector quantities.

 

Q.4.2 Pick out the two scalar quantities in the following list: force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.

Ans.4.2

Work & Current are scalar quantities. Work is the product of Force and displacement. Since the product of two vectors quantities are always scalar. Current is independent of direction, it is only magnitude, hence scalar.

 

Q.4.3 Pick out the only vector quantity in the following list: Temperature, pressure, impulse, time, power, total path length, energy

Ans.4.3

Impulse is the only vector quantity from the above list. Impulse is the product of force and time. Force is a vector quantity and time is a scalar quantity. The product of 1 vector and 1 scalar is always a vector quantity.

 

Q.4.4 State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:

(a) Adding any two scalars,

(b) Adding a scalar to a vector of the same dimensions,

(c) Multiplying any vector by any scalar,

(d) Multiplying any two scalars,

(e) Adding any two vectors,

(f) Adding a component of a vector to the same vector.

Ans.4.4

• The addition of two scalar quantities is meaningful – if they both represent the same physical quantity.
• The addition of a vector quantity with a scalar quantity is not meaningful.
• Multiplying a scalar with a vector is meaningful.
• The multiplication of two scalar quantities is meaningful.
• The addition of two vectors is meaningful.
• Adding a component of a vector to the same vector is meaningful.

 

Q.4.5 Read each statement below carefully and state with reasons, if it is true or false:

 (a) The magnitude of a vector is always a scalar,

(b) Each component of a vector is always a scalar,

(c) The total path length is always equal to the magnitude of the displacement vector of a particle.

(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time,

(e) Three vectors not lying in a plane can never add up to give a null vector.

Ans.4.5

• The magnitude of a vector is a number only, hence always a scalar – TRUE
• Each component of a vector is also a vector – FALSE
• The total path length is a scalar quantity, whereas displacement is a vector quantity. – FALSE
• The total path length is always greater than or equal to the magnitude of displacement of a particle – TRUE
• Three vectors which do not lie in a plane can never add up to give a null vector – TRUE

 

Q.4.6 Establish the following vector inequalities geometrically or otherwise:

(a) |a+b| < |a| + |b|

(b) |a+b| > ||a| −|b||

(c) |a−−b| < |a| + |b|

(d) |a−−b| > ||a| − |b||

When does the equality sign above apply?

 

Ans.4.6

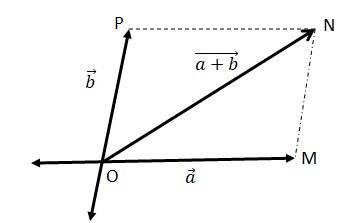
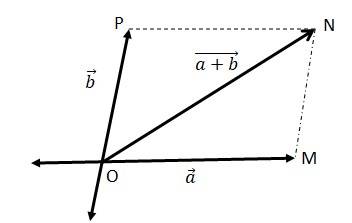
(a)

We can write

$\overline{\left|OM\right|}$ =  $\left|\vec{a}\right|\dots \dots \dots .\left(\mathrm{i}\right)$

$$  $\overline{\left|MN\right|}$ =  $\left|\vec{b}\right|$ =  $\overline{\left|OP\right|}$ ………(ii)

$$  $\overline{\left|ON\right|}$ =  $\left|\vec{a}+\vec{b}\right|\dots \dots .\left(iii\right)$

In a triangle, each side is smaller than the sum of the other two sides. Therefore in ΔOMN, we have ON < (OM + MN)

$\left|\vec{a}+\vec{b}\right|$ <  $\left|\vec{a}\right|$ +  $\left|\vec{b}\right|$ …..(iv)

If the two vectors  $\vec{a}$ and  $\vec{b}$ act along a straight line in the same direction, then we can write  $\left|\vec{a}+\vec{b}\right|$ =  $\left|\vec{a}\right|$ +  $\left|\vec{b}\right|\dots ..\left(v\right)$

Combining equations (iv) and (v), we get

$\left|\vec{a}+\vec{b}\right|$  $\le$  $\left|\vec{a}\right|$ +  $\left|\vec{b}\right|$

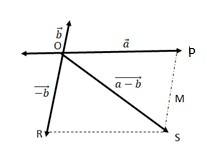
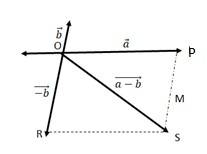
(b)

Let two vectors  $\vec{a}$ and  $\vec{b}$ be represented by the adjacent sides of a parallelogram OMNP.

We can write

$\overline{\left|OM\right|}$ =  $\left|\vec{a}\right|\dots \dots \dots .\left(\mathrm{i}\right)$

$$  $\overline{\left|MN\right|}$ =  $\left|\vec{b}\right|$ =  $\overline{\left|OP\right|}$ ………(ii)

$$  $\overline{\left|ON\right|}$ =  $\left|\vec{a}+\vec{b}\right|\dots \dots .\left(iii\right)$

In a triangle, each side is smaller than the sum of the other two sides. Therefore in ΔOMN, we have ON + MN > OM and ON + OM > MN

$$  $\overline{\left|ON\right|}>\left|\overline{OM-OP}\right|$

$\left|\vec{a}+\vec{b}\right|>$  $\left|\vec{a}\right|$ -  $\left|\vec{b}\right|$ ……(iv)

If the two vectors  $\vec{a}$ and  $\vec{b}$ act along a straight line in the same direction, then we can write  $\left|\vec{a}+\vec{b}\right|$ =  $\left|\vec{a}\right|$ -  $\left|\vec{b}\right|\dots ..\left(v\right)$

Combining (iv) and (v), we get:

$\left|\vec{a}+\vec{b}\right|\ge$  $\left|\vec{a}\right|$ -  $\left|\vec{b}\right|$

(c)

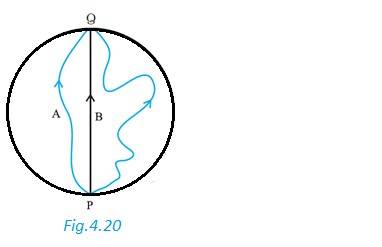
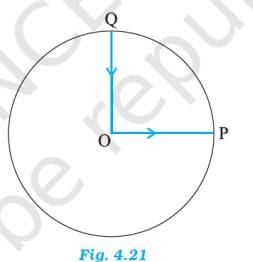
Q.4.9 A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes 10 min, what is the

(a) Net displacement, (b) average velocity, and (c) average speed of the cyclist?

Ans.4.9

Since the cyclist came back to his starting point O, so the displacement is Zero.

Average velocity =  $\frac{netdisplacement}{timetaken}=\frac{0}{timetaken}$ = 0

Average speed =  $\frac{distancetravelled}{timetaken}$

Distance travelled = OP + PQ + QO

= 1 + (1/4)  $\times 2\times \left(\frac{22}{7}\right)\times 1+1=$ 3.57 km

Average speed = 3.57 / 10 km/min = 21.43 km/h

 

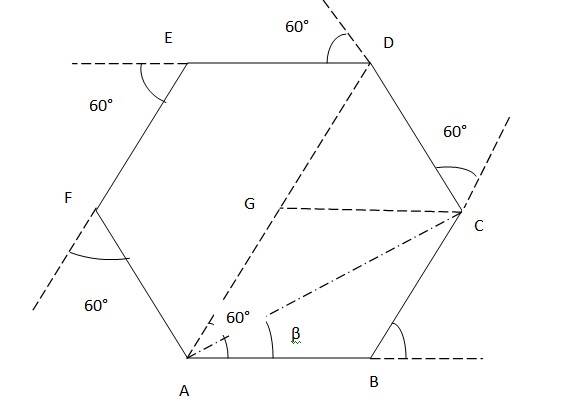
Q.4.10 On an open ground, a motorist follows a track that turns to his left by an angle of 60  $°$ after every 500 m. Starting from a given turn; specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.

Ans.4.10

Let the motorist start from point A. From A, he goes to B (first turn), then to C (second turn), then to D (third turn).

The magnitude of displacement = DG + GA = 500m + 500m = 1000m

Total path length = AB + BC + CD = 500m +500m +500m = 1500 m

The motorist takes the 6th turn at point A, which is his starting point. Therefore,

The magnitude of displacement = 0

Total path length = AB + BC + CD + DE + EF + FA = 500m + 500m +500m +500m + 500m + 500m = 3000m

The motorist takes the 8th turn at point C. The magnitude of displacement = AC

=  $\sqrt{{AB}^2+{BC}^2+2\left(AB\right)\times (BCCos60°)}$

= 866.03 m

tan β =  $\frac{500sin60°}{500+500\cos 60°}$ , β = tan-1(  $\frac{433.01}{750}$ )= 30  $°$

Hence the magnitude of displacement is 866.03m at an angle 30  $°$ with AB

Total path length = 600  $\times$ 500 + 500 +500 = 4000 m

 

Q.4.11 A passenger arriving in a new town wishes to go from the station to a hotel located 10 km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23 km long and reaches the hotel in 28 min. What is (a) the average speed of the taxi, (b) the magnitude of average velocity? Are the two equal?

Ans.4.11

Total distance travelled = 23 km, Total time taken = 28 min

Average speed =  $\frac{Totaldistancetravelled}{Totaltimetaken}$ =  $\frac{23}{28}$ km/min = 49.29 km/h

Average velocity =  $\frac{Totaldisplacement}{totaltimetaken}$ =  $\frac{10}{28}$ km/min = 21.43 km/h

 

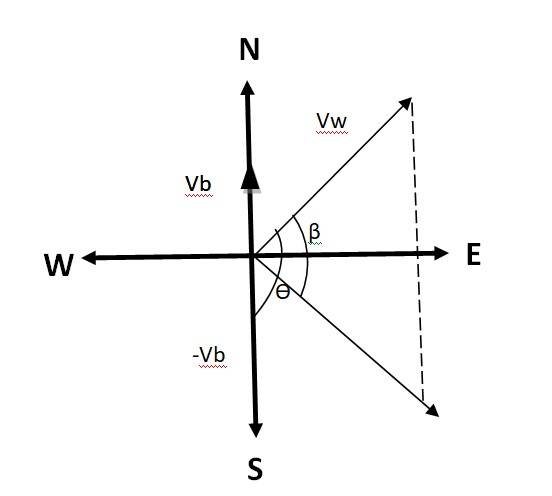
Q.4.12 Rain is falling vertically with a speed of 30 m s^-1. A woman rides a bicycle with a speed of 10 m s^-1 in the north to south direction. What is the direction in which she should hold her umbrella?

 

 

Let Vc = Velocity of the cyclist

Vr = Velocity of the rain

If V is the relative velocity, the woman must hold her umbrella in the direction of V.

V = Vr + (-Vc) = 30 + (-10) = 20 m/s

Tan  $\theta$ =  $\frac{Vc}{Vr}$ =  $\frac{10}{30}$ ,  $\theta$ = 18  $°$

 

Q.4.13 A man can swim with a speed of 4.0 km/h in still water. How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?

Ans.4.13

Swimming speed = 4 km/h, Width of the river = 1.0 km

Time required to cross the river =  $\frac{Widthoftheriver}{Swimmingspeed}$ =  $\frac{1}{4}$ h= 15 min

Speed of the river = 3 km/h

Distance covered by the river in 15 min = 3  $\times \left(\frac{15}{60}\right)$  $\times 1000$ = 750 m

 

Q.4.14 In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?

Ans.4.14

The velocity of the boat  $V_b$ = 51 km/h, the velocity of the wind  $V_w$ = 72 km/h

Flag is fluttering in N-E direction, so the  $V_w$ direction is N-E.

When the ship begins to sail towards North, the flag will flutter along the direction of relative velocity of the wind w.r.t. the boat.

The angle between  $V_w$ & -  $V_b$ = 90  $°+45°$

tan  $\beta$ =  $\frac{V_{b}sin(90+45)}{V_w+V_{b}cos(90+45)}$ =  $\frac{51\mathrm{s}\mathrm{i}\mathrm{n}(90+45)}{72+51\mathrm{c}\mathrm{o}\mathrm{s}(90+45)}$ =  $\frac{36.062}{35.937}$

$\beta =$ tan-1(  $\frac{36.062}{35.937}$ ) = 45.099  $°$

Angle with respect to East direction = 45.099  $°$ - 45  $°$ = 0.099  $°$

Hence the flag will flutter almost due East.

 

Q.4.15 The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s^-1 can go without hitting the ceiling of the hall?

Ans.4.15

The speed of the ball, u = 40 m/s

Ceiling height, h = 25m

Since the ball is thrown, it will follow the path of a projectile. For projectile motion, the maximum height for a body projected at an angle  $\theta$ is given by

h=  $\frac{u^2{sin}^2\theta }{2g}$ , sin2  $\theta$ = (25  $\times 2\times 9.807)/(40\times 40)$ ,  $\theta =33.61°$

Horizontal range is given by,=

R =  $\frac{u^2}{g}sin2\theta$ = ((40  $\times 40$ )  $\times \sin 2\times 33.61°$ )/9.81 = 150.38m

Q.4.16 A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?

Ans.4.16

We know for a projectile motion, horizontal range is given by

R =  $\frac{u^2}{g}sin2\theta$ , where R is the horizontal range, u is the velocity and  $\theta$ is the angle of projectile

So  $\frac{u^2}{g}$ = 100/sin 2  $\theta$

The cricketer will only be able to throw the ball to the maximum horizontal distance when the angle of projection  $\theta$ = 45  $°$ ,  $\frac{u^2}{g}$ = 100 …….(1)

The ball will achieve max height when it is thrown vertically upward. For such motion, final velocity v = 0

From the equation  $v^2$ -  $u^2$ =2gH, where acceleration a = -g, we get

0 -  $u^2$ = -2gH, H =  $\frac{u^2}{2g}$ =  $\frac{100}{2}$ = 50m

 

Q.4.17 A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?

Ans.4.17

Given, the length of the string, l = 80 cm, No. of revolution = 14, Time taken = 25 s

We know Frequency, v =  $\frac{No.ofrevolution}{timetaken}$ =  $\frac{14}{25}$ Hz

Angular frequency  $\omega$ = 2ԯv = 2  $\times$  $\frac{22}{7}$  $\times \frac{14}{25}$ rad/s = 3.52 rad/s

Centripetal acceleration ac =  ${\omega }^2$ r =  ${3.52}^2\times \frac{80}{100}$ m/s2 = 9.91 m/s2

The direction of acceleration is towards the centre.

 

Q.4.18 An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.

Ans.4.18

The radius of the loop, r = 1 km = 1000 m

Speed, v = 900 km/h = 250 m/s

Centripetal acceleration, ac =  $\frac{v^2}{r}$ = 250  $\times 250$ / 1000 m/s² = 62.5 m/s² =  $\frac{62.5}{9.817}$ g = 6.37g

 

Q.4.19 Read each statement below carefully and state, with reasons, if it is true or false:

(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre

(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point

(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector

Ans.4.19

The net acceleration of a particle in circular motion is always directed along the radius of the circle towards the centre (centripetal force), in the case of a circular uniform motion. Hence the statement is False.

The centrifugal force direction is always along the tangent, hence the statement is True.

In uniform circular motion, the direction of the acceleration vector points is always toward the centre of the circle. The average of these vectors over one cycle is a null vector. Hence the statement is True.

 

Q.4.20 The position of a particle is given by

r = 3.0t ĭ − 2.0t 2 ĵ + 4.0 ķ m

where t is in seconds and the coefficients have the proper units for r to be in meters.

(a) Find the v and a of the particle?

(b) What is the magnitude and direction of velocity of the particle at t = 2.0 s?

Ans.4.20

The position is given by  $\vec{r}$ = 3. 0t ĭ − 2.0t 2 ĵ + 4.0 ķ

The velocity v is given by  $\stackrel{⃑}{v}$ =  $\frac{d\vec{r}}{dt}$ =  $\frac{d}{dt}$ (3.0t ĭ − 2.0t 2 ĵ + 4.0 ķ)

$\stackrel{⃑}{v}$ = 3.0 ĭ – 4.0tĵ

Acceleration  $\stackrel{⃑}{a}$ =  $\frac{d\vec{v}}{dt}$ =  $\frac{d}{dt}$ (3.0 ĭ – 4.0tĵ) = – 4.0ĵ

At t = 2.0s

$\stackrel{⃑}{v}$ = 3.0 ĭ – 4.0tĵ

The magnitude of velocity is given by  $\left|\stackrel{⃑}{v}\right|$ = (3.02 +- 8.02)0.5 = 8.54 m/s

Direction,  $\theta$ =  ${\tan }^{-1}\frac{v_y}{v_x}$ =  ${\tan }^{-1}\frac{8}{3}$ = 69.44  $°$

 

Q.4.21 A particle starts from the origin at t = 0 s with a velocity of 10.0 ĵ m/s and moves in the x-y plane with a constant acceleration of (8.0 ĭ + 2.0 ĵ) m s^-2.

(a) At what time is the x- coordinates of the particle 16 m? What is the y-coordinate of the particle at that time?

(b) What is the speed of the particle at the time?

 

Ans.4.21:

Velocity ,  $\stackrel{⃑}{v}$ = 10.0 ĵ m/s

Acceleration,  $\stackrel{⃑}{a}$ = (8.0 ĭ + 2.0 ĵ) m s-2

We know  $\stackrel{⃑}{a}$ =  $\frac{d\vec{v}}{dt}$ = 8.0 ĭ + 2.0 ĵ

$\stackrel{⃑}{dv}$ = (8.0 ĭ + 2.0 ĵ)dt

Integrating both sides we get  $\vec{v}$ (t) = 8.0t ĭ + 2.0t ĵ +  $\vec{u}$ ,

Where,  $\vec{u}=$ velocity vector of the particle at t =0

$\stackrel{⃑}{v}=$ velocity vector of the particle at time t

But  $\stackrel{⃑}{v}$ =  $\frac{\underset{dr}{\to }}{dt}$

$\stackrel{⃑}{dr}$ =  $\stackrel{⃑}{v}$ dt

= (8.0t ĭ + 2.0t ĵ +  $\vec{u}$ )dt

Integrating both sides with the condition at t = 0, r =0 and at t =t, r = r

$\stackrel{⃑}{r}=$  $\vec{u}$ t + ½  $\times$ 8.0 t2 ĭ + ½  $\times$ 2.0  $\times$ t2 ĵ =  $\vec{u}$ t + 4.0 t2 ĭ + t2 ĵ

Substituting the value of  $\stackrel{⃑}{u}$ , we get

$\stackrel{⃑}{r}=$ ( 10.0 ĵ)t + 4.0 t2 ĭ + t2 ĵ . This equation can be expressed as

x ĭ + y ĵ = 4.0 t2 ĭ + ( 10.0t + t2) ĵ

Since the motion of the particle is confined to the x-y plane, on equating the coefficients of ĭ and ĵ, we get

x = 4.0 t2 and y = 10.0t + t2

t =  $\sqrt{x/4}$

When x = 16m, t = 2 s, y = 24m

Velocity of the particle

$\vec{v}$ (t) = 8.0t ĭ + 2.0t ĵ +  $\vec{u}$

At t = 2 s,

$\vec{v}$ (t) = 8.0  $\times$ 2 ĭ + 2.0  $\times 2$ ĵ + 10  $\times$ ĵ = 16 ĭ + 14 ĵ

The magnitude of  $\vec{v}$ (t) is given by

$\left|\mathrm{}\vec{v}\right|$ = ( 162 + 142)1/2 = 21.26 m/s

 

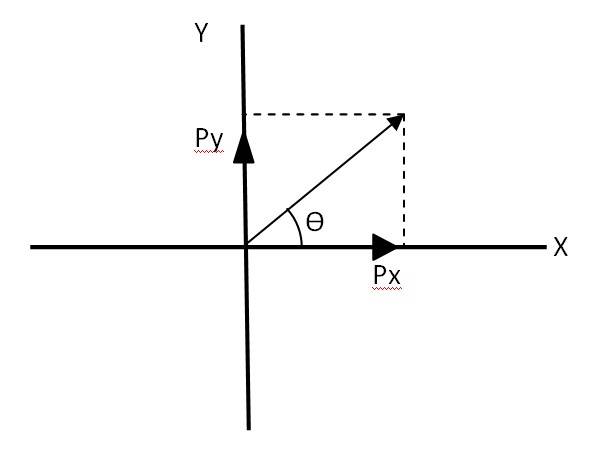
Q.4.22  $\stackrel{̂}{\mathit{i}}$ and  $\stackrel{̂}{\mathit{j}}$ are unit vectors along x- and y- axis respectively. What is the magnitude and direction of the vectors  $\stackrel{̂}{\mathit{i}}$ +  $\stackrel{̂}{\mathit{j}}$ , and  $\stackrel{̂}{\mathit{i}}$ -  $\stackrel{̂}{\mathit{j}}$ ? What are the components of a vector A= 2  $\stackrel{̂}{\mathit{i}}$ + 3  $\stackrel{̂}{\mathit{j}}$ along the directions of  $\stackrel{̂}{\mathit{i}}$ +  $\stackrel{̂}{\mathit{j}}$ , and  $\stackrel{̂}{\mathit{i}}$ -  $\stackrel{̂}{\mathit{j}}$ ? [You may use graphical method]

Ans.4.22

Let us consider a vector  $\vec{P}$ . The equation can be written as

Px = Py = 1  $\left|\vec{P}\right|$ =  $\surd (P_x^2+P_y^2)$  $\left|\vec{P}\right|$ =  $\surd (1^2+1^2)\left|\vec{P}\right|$ =  $\sqrt{2}$ …….(i)

So the magnitude of vector  $\vec{i}$ +  $\vec{j}$ =  $\sqrt{2}$

Let  $\theta$ be the angle made by vector  $\vec{P}$ , with the x axis as given in the above figure

$\tan \theta$ =  $\left(Px/Py\right)\theta$ =  ${\tan }^{-1}(1/1)$ ,  $\theta$ = 45  $°$ with the x axis

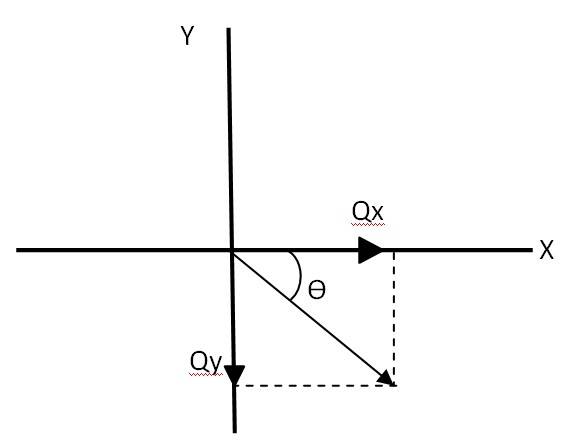
Let  $\vec{Q}$ =  $\stackrel{̂}{i}$ -  $\stackrel{̂}{j}$

$\overrightarrow{Q_x}\stackrel{̂}{i}$ –  $\overrightarrow{Q_y}$  $\stackrel{̂}{j}$ = (  $\stackrel{̂}{i}$ –  $\stackrel{̂}{j})$

$\overrightarrow{Q_x}$ =  $\overrightarrow{Q_y}$ = 1

$\left|\vec{Q}\right|$ =  $\sqrt{{Q_x}^2+{Q_y}^2}$ =  $\surd 2$

Hence  $\left|\vec{Q}\right|$ =  $\surd 2$ . Therefore the magnitude of (  $\stackrel{̂}{i}$ +  $\stackrel{̂}{j})$ =  $\surd 2$

Let  $\theta$ be the angle made by vector  $\vec{Q}$ , with the x axis as given in the above figure

$\tan \theta$ =  $\left(Qx/Qy\right)\theta$ =  ${-\tan }^{-1}(1/1)$ ,  $\theta$ = - 45  $°$ with the x axis

It is given that  $\vec{A}$ = 2  $\stackrel{̂}{i}$ + 3  $\stackrel{̂}{j}$ . We can write Ax  $\stackrel{̂}{i}$ + Ay  $\stackrel{̂}{j}$ = 2  $\stackrel{̂}{i}$ + 3  $\stackrel{̂}{j}$

Comparing the components on both sides, we get

Ax =2 and Ay = 3

$\left|\vec{A}\mathrm{}\right|$ =  $\sqrt{{(2}^2}+3^2$ ) =  $\surd 13$

Let  $\overrightarrow{A_x}$ make an angle  $\theta$ with the x axis, then

$\tan \theta$ = (Ax / Ay),  $\theta$ =  ${\tan }^{-1}(3/2)$ = 56.31  $°$

So the angle between (2  $\stackrel{̂}{i}$ + 3  $\stackrel{̂}{j}$ ) and (  $\stackrel{̂}{i}$ +  $\stackrel{̂}{j}$ )

$\theta \text{'}$ = 56.31 – 45 = 11.31  $°$

Component of vector  $\vec{A}$ , along the direction of  $\vec{P}$ , making an angle  $\theta$

= ( A cos  $\theta \text{'}$ )  $\stackrel{̂}{P}$

= ( A cos 11.31)  $\frac{(\mathrm{}\stackrel{̂}{i}+\stackrel{̂}{j}\mathrm{})}{\sqrt{2}}$

=  $\sqrt{13}$  $\times \frac{0.9806}{\sqrt{2}}$ (  $\stackrel{̂}{i}$ +  $\stackrel{̂}{j}$ )

= 2.5  $\times$  $\sqrt{2}$

=  $\frac{5}{\sqrt{2}}$

Let  $\theta \text{'}$ be the angle between the vectors (2  $\stackrel{̂}{i}$ + 3  $\stackrel{̂}{j}$ ) and (  $\stackrel{̂}{i}$ -  $\stackrel{̂}{j})$

$\theta "=45+56.31=101.31°$

Component of vector  $\vec{A}$ , along the direction of  $\vec{Q}$ , making an angle  $\theta$

= (A cos  $\theta "$ )  $\frac{\mathrm{}(\stackrel{̂}{i}\mathrm{}-\mathrm{}\stackrel{̂}{j})}{\sqrt{2}}$

=  $\sqrt{13}$ cos (  $101.31°)\frac{\mathrm{}(\stackrel{̂}{i}\mathrm{}-\mathrm{}\stackrel{̂}{j})}{\sqrt{2}}$

= -0.5(  $\stackrel{̂}{i}$ -  $\stackrel{̂}{j})$

=  $-\frac{1}{\sqrt{2}}$

 

Q.4.23 For any arbitrary motion in space, which of the following relations are true:

(a) v average = (1/2) (v (t1) + v (t2))

(b) v average = [r (t2) - r (t1)] / (t2 – t1)

(c) v (t) = v (0) + a t

(d) r (t) = r (0) + v (0) t + (1/2) a t²

(e) a average = [v (t2) - v (t1)] / (t2 – t1)

(The ‘average’ stands for average of the quantity over the time interval t1 to t2)

Ans.4.23

For any arbitrary motion of a particle average velocity cannot be expressed by this equation. False

The arbitrary motion of the particle can be represented by this equation, True.

For arbitrary motion of the particle, the acceleration may also be non uniform. False

The motion of the particle is arbitrary, acceleration of the particle may also be non-uniform, so can not represent the motion of the particle in space. False.

The arbitrary motion of the particle can be represented by the given equation. True.

 

Q.4. 24 Read each statement below carefully and state, with reasons and examples, if it is true or false:

A scalar quantity is one that

(a) is conserved in a process

(b) can never take negative values

(c) must be dimensionless

(d) does not vary from one point to another in space

(e) has the same value for observers with different orientations of axes.

Ans.4.24

Despite being a scalar quantity, energy is not conserved in elastic collisions. False.

Despite being a scalar quantity, the temperature can take negative values. False

The total path length is a scalar quantity. Yet it has the dimension of length. False

A scalar quantity such as gravitational potential can vary from one point to another point in space. False.

The value of a scalar does not vary for observers with different orientation of axis. True.

 

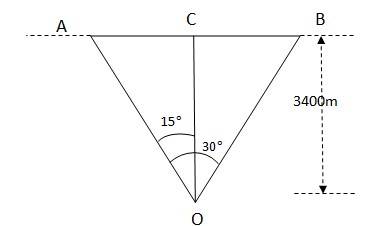
Q.4.25 An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is 30°, what is the speed of the aircraft?

Ans.4.25

Height of the aircraft from the ground = 3400m

Let A and B be the positions of the aircraft, making an angle of AOB = 30  $°$ . The perpendicular OC and OC is the height of the aircraft. Angles AOC = angle BOC = 15  $°$

In ΔAOC, AC = OC  $\tan 15°$ = 3400  $\tan 15°$ = 911.03m

AB = AC + CB = 2AC = 1822m

The distance of AB is covered in 10s, so the speed of the aircraft = 1822/10 m/s = 182.2 m/s

 

Q.4.26 A vector has magnitude and direction. Does it have a location in space? Can it vary with time? Will two equal vectors a and b at different locations in space necessarily have identical physical effects? Give examples in support of your answer.

Ans.4.26

Yes and No

A vector in space has no distinct location. The reason behind this is that a vector stays unchanged when it displaces in a way that its direction and magnitude do not change.

A vector changes with time. For instance, the velocity vector of a ball moving with a specific speed fluctuates with time.

Two equivalent vectors situated at different locations in space do not generate the same physical effect. For instance, two equivalent forces acting at different points on a body to rotate the body, but the combination will not generate the equivalent turning effect.

 

Q.4.27 A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?

Ans.4.27

No in the both the cases.

A physical quantity which is having both direction and magnitude is not necessarily a vector. For instance, in spite of having direction and magnitude, current is a scalar quantity. The basic necessity for a physical quantity to fall in a vector category is that it ought to follow the “law of vector addition”.

As the rotation of a body about an axis does not follow the basic necessity to be a vector i.e. it does not follow the “law of vector addition”.

 

Q.4.28 Can you associate vectors with

(a) the length of a wire bent into a loop,

(b) a plane area,

(c) a sphere?

Explain.

Ans.4.28

We cannot associate the length of a wire bent into a loop with a vector.

We can associate a plane area with a vector.

We cannot associate the volume of a sphere with a vector.

 

Q.4.29 A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.

Ans.4.29

The angle of projectile  $\theta$ = 30  $°$

The bullet hits the ground at a distance of 3 km, Range R = 3 km

We know horizontal range for a projectile motion, R =  $u^2$ sin2  $\theta$ / g

3 =  $u^2$ sin60  $°$ / g

$\frac{u^2}{g}$ = 3/ sin60  $°$ = 3.464 ……………(1)

To hit a target at 5 km,

Max Range,  $R_{max}$ =  $\frac{u^2}{g}$ …………..(2)

On comparing equation (1) and (2) , we get

$R_{max}$ = 3.464

Hence, the bullet will not hit the target even by adjusting its angle of projection.

 

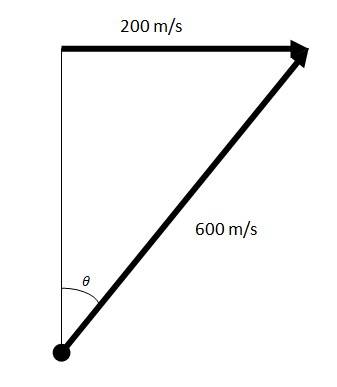
Q.4.30 A fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s^-1 to hit the plane ? At what minimum altitude should the pilot fly the plane to avoid being hit ? (Take g = 10 m s^-2 ).

Ans.4.30

Speed of the fighter plane = 720 km/h = 200 m/s

The altitude of the plane = 1.5 km =1500 m

Velocity of the shell = 600 m/s

$\sin \theta$ = 200/600

$\therefore \theta =19.47°$

Let H be the minimum altitude for the plane to fly, without being hit

Using equation H =  $u^2$ sin2(90-  $\theta )/2g$

= (6002cos2  $\theta$ )/2g

= 360000 {( 1 + cos2  $\theta$ )/2}/2  $\times$ 10

= 16000 m = 16 km

 

Q,4.31 A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?

Ans.4.31

Speed of the fighter plane = 720 km/h = 200 m/s

The altitude of the plane = 1.5 km =1500 m

Velocity of the shell = 600 m/s

$\sin \theta$ = 200/600

$\therefore \theta =19.47°$

Let H be the minimum altitude for the plane to fly, without being hit

Using equation H =  $u^2$ sin2(90-  $\theta )/2g$

= (6002cos2  $\theta$ )/2g

= 360000 {( 1 + cos2  $\theta$ )/2}/2  $\times$ 10

= 16000 m = 16 km

 

Q,4.31 A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?

Ans.4.31

Speed of the cyclist = 27 km/h = 7.5 m/s

Radius of the road = 80m

The net acceleration is due to braking and the centripetal acceleration

Acceleration due to braking = 0.5 m/s²

Centripetal acceleration a = v²r = (7.5)2/80= 0.703 m/s²

The resultant acceleration is given by a = sqrt (  $a_t^2$ +  $a_c^2$ ) = sqrt (  ${0.5}^2$ +  ${0.7}^2$ ) = 0.86 m/s²

tan  $\beta$ = ac / at = 0.7/0.5,  $\beta$ = 54.5  $°$

 

Q.4.32

(a) Show that for a projectile the angle between the velocity and the x-axis as a function

of time is given by

(b) Shows that the projection angle _0 for a projectile launched from the origin is

given by

where the symbols have their usual meaning.

Ans.4.32

Let  $\mathit{\theta }\left(\mathit{t}\right)=\mathit{}{\mathbf{tan}}^{-1}\left(\frac{{\mathit{v}}_{\mathit{o}\mathit{y}}-\mathit{}\mathit{g}\mathit{t}}{{\mathit{v}}_{\mathit{o}\mathit{x}}}\right)$ be the angle at which the projectile is fired w.r.t. the x-axis, since  ${\mathit{\theta }}_0=\mathit{}{\mathbf{tan}}^{-1}\left(\frac{4{\mathit{h}}_{\mathit{m}}}{\mathit{R}}\right)$ depends on t

Therefore tan  $\theta$ since (Vy=Voy -gt and Vx = Vox)

Since  $\theta$ =  $\theta \left(t\right)=\frac{Vx}{Vy}=\frac{Voy-gt}{Vox}$ sin2  $\theta \left(t\right)={\tan }^{-1}\left(\frac{Voy-gt}{Vox}\right)$ /2g…….(1)

R =  $h_{max}$ sin2  $u^2$ /g …….(2)

Dividing (1) by (2)

(  $\theta$ /R) = [  $u^2$ sin2  $\theta$ /2g]/[  $h_{max}$ sin2  $u^2$ /g] =  $\theta$ / 4