Waves Class 11 NCERT Solutions: Download Topic-wise Questions & Answers PDF

• Introduction to Waves
• Transverse and longitudinal waves
• Displacement relation in a progressive wave
• The speed of a travelling wave
• The principle of superposition of waves
• Reflection of waves
• Beats
• Doppler effect

Waves NCERT Solutions PDF download is provided here for the students. The students can download the PDF and refer later. The Physics NCERT Class 11 PDF for Waves chapter can be accessed by the student even if there is no internet connection. Therefore, PDF is very useful for students.

Download Here: NCERT Solution for Class XI Physics Chapter Waves PDF

Q.15.1 A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?

Ans. 15.1:

Mass of the string, M = 2.5 kg

Tension in the string, T = 200 N

Length of the string, l = 20 m

Mass per unit length,  $\mu$ =  $\frac{M}{l}$ =  $\frac{2.5}{20}$ = 0.125 kg/m

The velocity (v) of the transverse wave in the string is given by the relation:

$v=\sqrt{\frac{T}{\mu }}$ =  $\sqrt{\frac{200}{0.125}}$ = 40 m/s

Therefore, time taken by the disturbance to reach the other end, t =  $\frac{l}{v}$ =  $\frac{20}{40}$ = 0.5 s

Q.15.2 A stone dropped from the top of a tower of height 300 m splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s^–1? (g = 9.8 m s^–2)

Ans.15.2:

Height of the tower, h = 300 m

Initial velocity of the stone, u = 0

Acceleration, a = g = 9.8 m/  $s^2$

Speed of sound in air, V = 340 m/s

The time taken by the stone (t), to strike the water can be calculated from the relation

s =us +  $\frac{1}{2}$ a  $t^2$ as

300 = 0 +  $\frac{1}{2}\times 9.8\times t^2$ or t = 7.82 s

Time taken by the sound to reach the top of the tower,  $t_1$ =  $\frac{h}{V}$ =  $\frac{300}{340}$ = 0.88 s

Therefore, the time when the splash can be heard = 7.82 + 0.88 = 8.7 s

Q.15.3 A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s^–1.

Ans. 15.3:

Length of the steel wire, l = 12 m

Mass of the steel wire, m = 2.1 kg

Velocity of the transverse wave, v = 343 m/s

Mass per unit length,  $\mu$ =  $\frac{m}{l}$ =  $\frac{2.1}{12}$ = 0.175 kg/m

The velocity (v) of the transverse wave in the string is given by the relation:

$v=\sqrt{\frac{T}{\mu }}$ , where T is the tension

T =  $v^2\times \mu$ =  ${343}^2\times 0.175$ = 20588.575 N = 2.06  $\times {10}^4$ N

Q.15.4 Use the formula  $\mathit{v}=\sqrt{\frac{\mathit{\gamma }\mathit{P}}{\mathit{\rho }}}\mathit{}\mathit{}$ to explain why the speed of sound in air

(a) is independent of pressure,

(b) increases with temperature,

(c) increases with humidity.

Ans.15.4:

In the equation  $v=\sqrt{\frac{\gamma P}{\rho }}$ ……(i)

$\rho$ Density =  $\frac{Mass}{Volume}$ =  $\frac{M}{V}$ where M = molecular weight of the gas, V = Volume of the gas, so we can write

$v=\sqrt{\frac{\gamma PV}{M}}$ ……..(ii)

For ideal gas equation, PV = nRT, n = 1 so PV = RT

For constant T, PV = constant

In equation (ii), since PV = constant,  $\gamma$ and M constant, v is also constant. Hence, at a constant temperature, the speed of sound in a gaseous medium is independent of the change in the pressure of the gas.

From equation (i)  $v=\sqrt{\frac{\gamma P}{\rho }}$

For 1 mole of an ideal gas, the gas equation can be written as PV = RT or P =  $\frac{RT}{V}$

Substituting in equation (i), we get  $v=\sqrt{\frac{\gamma RT}{\rho V}}$ =  $\sqrt{\frac{\gamma RT}{M}}$

Since  $\gamma$ , R and M are constant, we get v  $\propto \surd T$

Hence, the speed of sound in a gas is directly proportional to the square root of the temperature of the gaseous medium. i.e. the speed of sound increase with an increase in the temperature of the gaseous medium and vice versa.

Let  $v_m$ and  $v_d$ be the speed of sound in moist air and dry air respectively and  ${\rho }_m$ and  ${\rho }_d$ be the corresponding densities

From equation (i)  $v=\sqrt{\frac{\gamma P}{\rho }}$ , we get  $v_m\mathrm{}=\sqrt{\frac{\gamma P}{{\rho }_m}}$ and  $v_d\mathrm{}=\sqrt{\frac{\gamma P}{{\rho }_d}}$

$\frac{v_m}{v_d}$ =  $\sqrt{\frac{{\rho }_d}{{\rho }_m}}$

However, the presence of water vapour reduces the density of air, i.e.  ${\rho }_d<$  ${\rho }_m$ , so  $v_m<$  $v_d$

Q.15.5 You have learnt that a travelling wave in one dimension is represented by a function y = f (x, t) where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:

(a) (x – vt )²

(b) log [(x + vt)/x₀]

(c) 1/(x + vt)

• For x =0 and t=0, the function (x – vt )² becomes 0

Hence for x=0 and t=0, the function represents a point and not a wave.

For x =0 and t=0, the function  $\log \frac{x+vt}{x_0}$ = log 0 =  $\propto$

Since the function does not converge to a finite value for x =0 and t = 0, it represents a travelling wave.

For x = 0 and t = 0, the function  $\frac{1}{x+vt}$ =  $\frac{1}{0}$ =  $\propto$

Since the function does not converge to a finite value for x = 0 and t = 0, it does not represent a travelling wave.

Q.15.6 A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound? Speed of sound in air is 340 m s ^–1 and in water 1486 m s^–1.

Ans.15.6:

Frequency of ultrasound,  $\nu$ = 1000 kHz =  ${10}^6$ Hz

Speed of sound in air,  $v_a$ = 340 m/s

Speed of sound in water,  $v_w$ = 1486 m/s

The wavelength of the reflected sound is given by the relation

${\lambda }_r=\frac{v_a}{\nu }$ =  $\frac{340}{{10}^6}$ = 3.4  $\times {10}^{-4}$ m

The wavelength of the transmitted sound wave is given by

${\lambda }_t=\frac{v_w}{\nu }$ =  $\frac{1486}{{10}^6}$ = 1.486  $\times {10}^{-3}$ m

Q.15.7 A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s^–1 ? The operating frequency of the scanner is 4.2 MHz.

Ans.15.7:

Speed of sound in tissue, v = 1.7 km/s = 1.7  $\times {10}^3$ m/s

Operating frequency of the scanner,  $\nu$ = 4.2 MHz = 4.2  $\times {10}^6$ Hz

The wavelength of sound in the tissue is given as:

$\lambda =\frac{v}{\nu }$ =  $\frac{1.7\mathrm{}\times {10}^3}{4.2\mathrm{}\times {10}^6}$ = 4.05  $\times {10}^{-4}$ m

Q.15.8 A transverse harmonic wave on a string is described by

y(x, t) = 3.0 sin (36 t + 0.018 x +  $\mathit{\pi }$ /4)

where x and y are in cm and t in s. The positive direction of x is from left to right.

(a) Is this a travelling wave or a stationary wave? If it is travelling, what are the speed and direction of its propagation?

(b) What are its amplitude and frequency?

(c) What is the initial phase at the origin?

(d) What is the least distance between two successive crests in the wave?

Ans.15.8:

The equation of a progressive wave travelling from right to left is given by the displacement function:

y (x, t) = a  $\sin (\omega t+kx+\phi )$ ……….(i)

The given equation is

y(x, t) = 3.0 sin (36 t + 0.018 x +  $\pi$ /4) …….(ii)

On comparing equations (i) and (ii), we find that the equation (ii) represents a travelling wave, propagating from right to left. Now, using equations (i) and (ii), we can write

$\omega =36rad/s$ , k = 0.018  $m^{-1}$

From the relation  $\nu =\frac{\omega }{2\pi }$ and  $\lambda =\frac{2\pi }{k}$ and v =  $\nu \lambda$ , we can write

v =  $\frac{\omega }{2\pi }\times$  $\frac{2\pi }{k}$ =  $\frac{\omega }{k}$ =  $\frac{36}{0.018}$ = 2000 cm /s = 20 m/s

Hence, the speed of the given travelling wave is 20 m/s

The frequency  $\nu =\frac{\omega }{2\pi }$ =  $\frac{36}{2\pi }$ = 5.73 Hz

Comparing equation (i) and (ii), we get

$\phi$ =  $\frac{\pi }{4}$

The distance between two successive crests or troughs is equal to the wavelength of the wave.

Wavelength  $\lambda =\frac{2\pi }{k}$ =  $\frac{2\pi }{0.018}$ = 349.07 cm = 3.49 m

Q.15.9 For the wave described in Exercise 15.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase ?

Ans.15.9:

All the waves have different phases. The given transverse harmonic wave is:

y(x, t) = 3.0 sin (36t + 0.018x +  $\frac{\pi }{4}$ ) ………(i)

For x = 0, the equation reduces to

y (0,t) = 3.0 sin (36t +  $\frac{\pi }{4}$ )

Also  $\omega$ =  $\frac{2\pi }{T}$ , so T =  $\frac{2\pi }{\omega }$ =  $\frac{2\pi }{36}$ =  $\frac{\pi }{18}$ s

For plotting y vs., t graphs using different values of t, we get

When t = 0, y = 2.12

t =  $\frac{T}{8}$ =  $\frac{\pi }{18\times 8}$ , y = 3

t =  $\frac{2T}{8}$ =  $\frac{2\times \pi }{18\times 8}$ , y = 2.12

t =  $\frac{3T}{8}$ =  $\frac{3\times \pi }{18\times 8}$ , y = 0

t =  $\frac{4T}{8}$ =  $\frac{4\times \pi }{18\times 8}$ , y = -2.12

t =  $\frac{5T}{8}$ =  $\frac{5\times \pi }{18\times 8}$ , y = -3

t =  $\frac{6T}{8}$ =  $\frac{6\times \pi }{18\times 8}$ , y = -2.12

t =  $\frac{7T}{8}$ =  $\frac{7\times \pi }{18\times 8}$ , y = 0

For x = 2 and x = 4. The phases of the three waves will get changed, frequency and amplitude will remain unchanged for any change of x.

Q.15.10 For the travelling harmonic wave

y(x, t) = 2.0 cos 2  (10t – 0.0080 x + 0.35)

where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of

(a) 4 m,

(b) 0.5 m,

(c)  /2,

(d) 3  /4

Ans.15.10

The equation for a travelling harmonic wave is given by

y(x, t) = 2.0 cos 2  $\pi$ (10t – 0.0080 x + 0.35) or

= 2.0 cos (20  $\pi$ t – 0.016  $\pi$ x + 0.70  $\pi$ )

Comparing with classical equation y (x, t) = a  $\sin (\omega t+kx+\phi )$ , we get

Amplitude a = 2.0 cm. Propagation constant, k = 0.016  $\pi$ , angular frequent,  $\omega =20\pi rad/s$

From the relation  $\phi =kx=\frac{2\pi }{\lambda }x$

For x = 4 m = 400 cm, we have  $\phi$ = 0.016  $\pi \times 400$ = 6.4  $\pi$ rad

For x = 0.5 m = 50 cm, we have  $\phi$ = 0.016  $\pi \times 50$ = 0.8  $\pi$ rad

For x =  $\frac{\lambda }{2}$ , we have  $\phi =\frac{2\pi }{\lambda }\times$  $\frac{\lambda }{2}$ =  $\pi$ rad

For x =  $\frac{3\lambda }{4}$ , we have  $\phi =\frac{2\pi }{\lambda }\times$  $\frac{3\lambda }{4}$ =  $1.5\pi$ rad

Q.15.11 The transverse displacement of a string (clamped at its both ends) is given by

y(x, t) = 0.06 sin(  $\frac{2\mathit{\pi }}{3}\mathit{x})$ cos (120  $\mathit{\pi }\mathit{t})$

where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 ×10^–2 kg.

Answer the following :

(a) Does the function represent a travelling wave or a stationary wave?

(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What are the wavelength, frequency, and speed of each wave ?

 (c) Determine the tension in the string

Ans.15.11

The general equation representing a stationary wave is given by the displacement function y(x,t) = 2asin kx cos  $\omega t$

The equation is similar to the give equation y(x, t) = 0.06 sin (  $\frac{2\pi }{3}x)$ cos (120  $\pi t)$

Hence, the given function represents a stationary wave.

A wave travelling along the positive x-direction is given as:  $y_1$ = asin (  $\omega$ t – kx)

The wave travelling along the negative x-direction is given as:  $y_2$ = asin (  $\omega$ t + kx)

The superposition of these two waves yields:

y =  $y_1+y_2$ = asin (  $\omega$ t – kx) + asin (  $\omega$ t + kx)

= a sin(  $\omega$ t)cos(kx) – a sin(kx)cos(  $\omega$ t) – asin(  $\omega$ t)cos(kx) – asin(kx)cos(  $\omega$ t)

= -2a sin (kx) cos (  $\omega$ t)

= -2asin(  $\frac{2\pi }{\lambda }$ x) cos (2  $\pi \nu$ t) ……..(i)

The transverse displacement of the string is given as

y(x, t) = 0.06 sin (  $\frac{2\pi }{3}x)$ cos (120  $\pi t)\dots \dots \dots$ (ii)

Comparing equations (i) and (ii), we have  $\frac{2\pi }{\lambda }$ =  $\frac{2\pi }{3}$

Therefore  $\lambda$ = 3m, it is given that 120  $\pi$ = 2  $\pi \nu$ so Frequency,  $\nu =60\mathrm{H}\mathrm{z}$

Wave speed, v =  $\nu \lambda$ = 60  $\times 3$ = 180 m/s

The velocity of a transverse wave travelling in a string is given by the relation:

v =  $\sqrt{\frac{T}{\mu }}$ ….(i)

We have v = 180 m/s, mass of the string, m = 3  $\times {10}^{-2}$ kg,

length of the string, l = 1.5 m

Mass per unit length of the string,  $\mu$ = m/l =  $\frac{3}{1.5}\times {10}^{-2}$ =  $2\times {10}^{-2}$ kg/m

Tension in the string, T =  $v^2$  $\times \mu ={180}^2$  $\times 2\times {10}^{-2}$ = 648 N

Q.15.12 (i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers.

(ii) What is the amplitude of a point 0.375 m away from one end

Ans.15.12

(i)

(a) All the points on the string oscillates with the same frequency, except at the nodes, which have zero frequency

(b) All the points in any vibrating loop have the same phase, except at the nodes.

(c) All the points in any vibrating loop will have different amplitudes of vibration.

(ii)

The given equation is: y(x, t) = 0.06 sin (  $\frac{2\pi }{3}x)$ cos (120  $\pi t)$

For x = 0.375 and t =0

Amplitude = Displacement = 0.06 sin (  $\frac{2\pi }{3}\times \times 0.375)$ cos (0  $)$ = 0.06sin (  $\frac{\pi }{4})$ = 0.042 m

Q.15.13 Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all:

(a) y = 2 cos (3x) sin (10t)

(b) y = 2

(c) y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)

(d) y = cos x sin t + cos 2x sin 2t

Ans.15.13

The given equation represents a stationary wave because the harmonic terms kx and  $\omega t$ appear separately in the equation.

The given equation does not contain any harmonic term. Therefore, it does not represent either a travelling wave or a stationary wave.

The given equation represents a travelling wave as the harmonic terms kx and  $\omega t$ are in the combination of kx –  $\omega t$ .

The given equation represents a stationary wave because the harmonic terms kx and  $\omega t\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{}\mathrm{s}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{l}\mathrm{y}$ in the equation. This equation represents the superposition of two stationary waves.

Q.15.14 A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10^–2 kg and its linear mass density is 4.0 × 10^–2 kg m^–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?

Ans.15.14

Mass of the wire, m = 3.5  $\times {10}^{-2}$ kg

Linear mass density,  $\mu =\frac{m}{l}$ = 4  $\times {10}^{-2}$ kg/m

Frequency of vibration,  $\nu$ = 45 Hz

Length of the wire, l =  $\frac{m}{\mu }$ =  $\frac{3.5\mathrm{}\times {10}^{-2}}{4\mathrm{}\times {10}^{-2}}$ = 0.875 m

The wavelength of the stationary wave  $\lambda$ =  $\frac{2l}{n}$ , where n = number of nodes in the wire

For fundamental node, n = 1,  $\lambda$ = 2l = 2  $\times 0.875=1.75m$

The speed of the transverse wave in the string is given as v =  $\nu \lambda$ = 45  $\times 1.75$ = 78.75 m/s

The tension produced in the string is given by the relation, T =  $v^2\mu$ =  ${\left(78.75\right)}^2$  $\times$ 4  $\times {10}^{-2}$ = 248.06 N

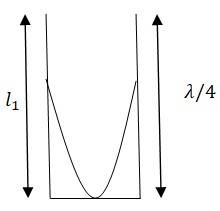
Q.15.15 A meter-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.

Ans.15.15

Frequency of the tuning fork,  $\nu$ = 340 Hz

Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in this figure.

$l_1$ =  $\frac{\lambda }{4},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}$ of the pipe  $l_1$ = 25.5 cm = 0.255 m

$\lambda =4l_1$ = 4  $\times 0.255$ m = 1.02 m

The speed of sound is given by the relation, v =  $\nu \lambda$ = 340  $\times 1.02$ = 346.8 m/s

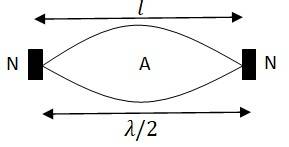
Q.15.16 A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of sound in steel?

Ans.15.16

Length of the steel rod, l = 100 cm = 1 m

Fundamental frequency of vibration,  $\nu$ = 2.53 kHz = 2.53  $\times {10}^3$ Hz

When the rod is plucked at its middle, an antinode (A) is formed at the centre, and the nodes (N) are formed at its two ends, as shown in the figure.

The distance between two successive nodes is  $\lambda$  $/2$

l =  $\lambda /2$  $\lambda$ = 2l = 2 m

The speed of sound in steel is given by the relation

v =  $\nu \lambda$ = 2.53  $\times {10}^3\times 2$ = 5.06  $\times {10}^3$ m/s = 5.06 km/s

 

Q.15.17 A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (speed of sound in air is 340 m s^–1).

Ans.15.17

Length of the pipe, l = 20 cm = 0.2 m

Source frequency =  $n^{th}$ normal mode frequency is given by the relation

${\nu }_n$ = (2n-1)  $\frac{\nu }{4l}$ , n is an integer = 0,1,2,3,…..

430 = (2n-1)  $\times \frac{340}{4\times 0.2}$

n = 1

Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the  $n^{th}$ mode of vibration frequency is given by the relation:

${\nu }_n=\frac{nv}{2l}$ , n =  $\frac{2l{\nu }_n}{v}$ =  $\frac{2\times 0.2\times 430}{340}$ = 0.5

Since the number of the node of vibration (n) has to be an integer, the given source does not produce a resound vibration in an open pipe.

Q.15.18 Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in the string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?

Ans.15.18

Frequency of string A,  $f_A$ = 324 Hz, let the frequency of string B, be =  $f_B$

Beat’s frequency, n = 6 Hz

Beat’s frequency is given as n =  $\left|f_A\pm f_B\right|$ or 6 = 324  $\pm f_B$

$f_B=318Hzor330Hz$

Frequency decreases with a decrease in the tension in a string. This is because frequency is directly proportional to the square root of tension,. It is given as

$\nu \propto \surd T$

Hence the beat frequency cannot be 330 Hz. So  $f_B=318Hz$

 

Q.15.19 Explain why (or how):

(a) in a sound wave, a displacement node is a pressure antinode and vice versa,

(b) bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,

(c) a violin note and sitar note may have the same frequency, yet we can distinguish between the two notes,

(d) solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases, and

(e) the shape of a pulse gets distorted during propagation in a dispersive medium.

Ans.15.19

• A node is a point where the amplitude of vibration is the minimum and the pressure is maximum. On the other hand, an antinode is a point where the amplitude of vibration is maximum and the pressure is minimum. Therefore, a displacement node is nothing but a pressure antinode and vice versa.
• Bats emit very high-frequency ultrasonic sound waves. These waves get reflected back toward them by obstacles. A bat receives a reflected wave (frequency) and estimates the distance, direction, nature and size of the obstacle with the help of its brain senses.
• The overtone produced by a sitar and a violin, and the strengths of these overtones, are different. Hence, one can distinguish between the notes produced by a sitar and a violin even if they have the same frequency of vibration.
• Solids have shear modulus. They can sustain shearing stresses. Since fluids do not have any definite shape, they yield to shearing stress. The propagation of a transverse waves is such that it produces shearing stress in a medium. The propagation of such wave is possible only in solids, and not in gases. Both solids and fluids have their respective bulk moduli. They can sustain compressive stress. Hence, longitudinal waves can propagate through solids and fluids.
• A pulse is actually being a combination of waves having different wavelengths. These waves travel in a dispersive medium with different velocities, depending on the nature of the medium. This results in the distortion of the shape of a wave pulse.

 

Q.15.20 A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air.

(i) What is the frequency of the whistle for a platform observer when the train

(a) approaches the platform with a speed of 10 m s^–1,

(b) recedes from the platform with a speed of 10 m s^–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s^–1.

 Ans.15.20

Frequency of the whistle,  $\nu$ = 400 Hz

Speed of the train,  $v_r$ = 10 m/s

Speed of sound, v = 340 m/s

The apparent frequency (f’) of the whistle as the train approaches the platform is given by the relation:

f’ = (  $\frac{v}{v-v_r})\nu$ = (  $\frac{340}{340-10})\times 400=$ 412.12 Hz

The apparent frequency (f”) of the whistle as the train recedes from the platform is given by the relation:

f” = (  $\frac{v}{v+v_r})\nu$ = (  $\frac{340}{340+10})\times 400=$ 388.57 Hz

The apparent change in the frequency of sound is caused by the relative motions of the source and the observer. These relative motions produce no effect on the speed of sound.

Therefore, the speed of sound in air in both the cases remains the same, i.e. 340 m/s.

 

Q.15.21 A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with a speed of 10 m s^–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s^–1? The speed of sound in still air can be taken as 340 m s^–1

Ans.15.21

• For the stationary observer:

Frequency of the sound produced by the whistle,  = 400 Hz

Speed of sound = 340 m/s

Velocity of wind, v = 10 m/s

As there is no relative motion between the source and the observer, the frequency of the sound heard by the observer will be the same as that produced by the source, i.e. 400 Hz. The wind is blowing towards the observer. Hence, the effective speed of the sound increases by 10 units, i.e.

Effective speed of the sound,  $v_e$ = 340 + 10 = 350 m/s

The wavelength (  $\lambda )\mathrm{o}\mathrm{f}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}$ heard by the observer is given by the relation:

$\lambda =\frac{v_e}{\nu }$ =  $\frac{350}{400}$ = 0.875 m

$\left(\mathrm{b}\right)$ For the running Observer:

$\mathrm{V}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{r}$ ,  $v_o$ = 10 m/s

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{r}$ is moving towards the source. As a result of the relative motions of the source and the observer, there is a change in frequency (f’’’)

$\mathrm{T}\mathrm{h}\mathrm{i}\mathrm{s}\mathrm{}\mathrm{i}\mathrm{s}\mathrm{}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{}\mathrm{b}\mathrm{y}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:$ f’’’ = (  $\frac{v+v_o}{v})\nu$ = (  $\frac{340+10}{340})\times 400=$ 411.76 Hz

Since the air is still, the effective speed of sound = 340 + 0 = 340 m/s

The source is at rest. Therefore, the wavelength of the sound will not change, i.e.  $\lambda$ remains 0.875 m.

Hence, the given two situations are not exactly identical.

Q.15.22 A travelling harmonic wave on a string is described by

y(x, t) = 7.5 sin (0.0050x +12t +  $\mathit{\pi }$ /4)

(a) what are the displacement and velocity of oscillation of a point at x = 1 cm, and t = 1 s? Is this velocity equal to the velocity of wave propagation?

(b)Locate the points of the string which have the same transverse displacements and velocity as the x = 1 cm point at t = 2 s, 5 s and 11 s.

Ans.15.22

The given harmonic wave is

y(x, t) = 7.5 sin (0.0050x +12t +  $\pi$ /4)

For x = 1 cm and t = 1 s

y(1, 1) = 7.5 sin (0.0050 +12+  $\mathrm{\pi }$ /4)

= 7.5 sin( 12.0050 +  $\frac{\pi }{4}$ )

= 7.5 sin (12.0050 + 0.7854)

= 7.5 sin (732.84  $°$ )

= 7.5 sin (90  $\times 8+$ 12.81)  $°$

= 7.5 sin 12.81  $°$

=1.6629 cm

The velocity of the oscillation at a given point and the time is given as:

v =  $\frac{d}{dt}$ y(x,t) =  $\frac{d}{dt}\left[7.5\mathrm{}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{}(0.0050x+12t+\pi /4)\right]$

= 7.5  $\times 12\mathrm{c}\mathrm{o}\mathrm{s}(0.0050x+12t+\pi /4$ )

At x= 1 cm and t= 1 s

v= y (1,1) = 90 cos (12.005 +  $\frac{\pi }{4}$ ) = 90 cos(12.81  $°$ ) = 87.75 cm/s

Now the equation of a propagating wave is given by

Y(x, t) = a sin (kx +  $\omega$ t +  $\phi )$ , where

k =  $\frac{2\pi }{\lambda }$ or  $\lambda$ =  $\frac{2\pi }{k}$ and  $\omega =2\pi v$

Speed, v =  $\frac{\omega }{k}$ , where  $\omega$ = 12 rad/s and k = 0.0050 /m

v =  $\frac{12}{0.0050}$ = 2400 cm/s

Hence, the velocity of the wave oscillation at x=1 cm and t=1s is not equal to the velocity of the wave propagation.

Propagation constant is related to wavelength as:

$\lambda$ =  $\frac{2\pi }{k}$ =  $\frac{2\pi }{0.0050}$ = 1256 cm = 12.56 m

Therefore, all the points at distances n  $\lambda$ (n =  $\pm 1,\pm 2\dots \dots .\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{}\mathrm{s}\mathrm{o}\mathrm{}\mathrm{o}\mathrm{n})$ i.e.  $\pm 12.56m,\pm 25.12m\dots \dots .$ and so on for x=1 cm, will have the same displacement as the x=1 cm points at t= 2s, 5s and 11s.

 

Q.15.23 A narrow sound pulse (for example, a short pip by a whistle) is sent across a medium. (a) Does the pulse have a definite (i) frequency, (ii) wavelength, (iii) speed of propagation? (b) If the pulse rate is 1 after every 20 s, (that is the whistle is blown for a split of second after every 20 s), is the frequency of the note produced by the whistle equal to 1/20 or 0.05 Hz ?

 

Ans.15.23 

The narrow sound pulse does not have a fixed wavelength or frequency. However, the speed of the sound pulse remains the same, which is equal to the speed in that medium. The short pip produced after 20 s does not mean that the frequency of the whistle is  $\frac{1}{20}\mathrm{o}\mathrm{r}$ 0.05 Hz. It means that 0.05 Hz is the frequency of repetition of the pip of the whistle. So the answers are

(i) No

(ii) No

(iii) Yes

No

 

Q.15.24 One end of a long string of linear mass density 8.0 × 10^–3 kg m^–1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t = 0, the left end (fork end) of the string x = 0 has zero transverse displacement (y = 0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.

 

Ans.15.24

The equation of a travelling wave propagating along the positive y- direction is given by the displacement equation:

y(x, t) = a sin (  $\omega t-kx)$ ………(i)

Linear mass density  $\mu =$ 8.0  $\times {10}^{-3}$ kg/m and frequency of the tuning fork,  $\nu$ = 256 Hz

Amplitude of the wave, a= 5.0 cm = 0.05 m …..(ii)

Mass of the pan, m = 90 kg and tension of the string, T = mg = 90  $\times 9.8$ = 882 N

The velocity of the transverse wave, v is given by the relation:

v =  $\sqrt{\frac{T}{\mu }}$ =  $\sqrt{\frac{882}{8.0\mathrm{}\times {10}^{-3}}}$ = 332 m/s

Angular frequency,  $\omega$ = 2  $\pi \nu$ = 2  $\pi \times 256$ = 1608.5 rad/s = 1.6  $\times {10}^3$ rad/s

Wavelength,  $\lambda$ =  $\frac{v}{\nu }$ =  $\frac{332}{256}$ = 1.297 m

Propagation constant, k =  $\frac{2\pi }{\lambda }$ =  $\frac{2\pi }{1.297}$ = 4.844 /m

Substituting these values in the displacement equation, we get

y(x,t) = a sin(  $\omega t-kx)$

y(x,t) = 0.05 sin(1.6  $\times {10}^3$ t – 4.844 x) m

 

Q.15.25 A SONAR system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h^–1. What is the frequency of sound reflected by the submarine ? Take the speed of sound in water to be 1450 m s^–1

Ans.15.25

Operating frequency of the SONAR system,  $\nu$ = 40 kHz

Speed of enemy submarine,  $v_e=$ 360 km/h = 100 m/s

Speed of sound in water, v = 1450 m/s

The source is at rest and the observer (enemy submarine) is moving towards it. Hence, the apparent frequency (f’) received and reflected by the submarine is given by the relation:

f = (  $\frac{v+v_e}{v})\nu =$ (  $\frac{1450+100}{1450})\times 40$ = 42.76 kHz

The frequency (f’) received by the enemy submarine is given by the relation:

f’ = (  $\frac{v}{v-v_e}$ )f = (  $\frac{1450}{1450-100}$ )  $\times 42.76$ = 45.93 kHz

 

Q.15.26 Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s^–1, and that of P wave is 8.0 km s^–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur ?

 

Ans.15.26

Let  $v_s$ and  $v_p$ be the velocities and  $t_s$ and  $t_p$ be the time taken to reach the seismograph from the epicentre of S and P waves respectively.

Let L be the distance between the epicentre and the seismograph.

We have:

L =  $v_s{t}_s$ ….(i)

L =  $v_p{t}_p$ ….(ii)

It is given,  $v_s$ = 4 km/s and  $v_p$ = 8 km/s

From equation (i) and (ii), we get

4  $t_s$ = 8  $t_p$ or  $t_s=$ 2  $t_p$ …..(iii)

It is also given,

$t_s-t_p=240s$ so  $t_p=240sand{t}_s=480s$

From equation (ii), we get, L = 8  $\times 240$ = 1920 km

Hence, the earthquake occurred at a distance of 1920 km from the seismograph.

 

Q.15.27 A bat is flitting about in a cave, navigating via ultrasonic beeps. Assume that the sound emission frequency of the bat is 40 kHz. During one fast swoop directly toward a flat wall surface, the bat is moving at 0.03 times the speed of sound in air. What frequency does the bat hear reflected off the wall?

Ans.15.27

Ultrasonic beep frequency emitted by bat,  $\nu$ = 40 kHz

Velocity of the bat,  $v_b$ = 0.03v, where v = velocity of sound in air

The apparent frequency of the sound striking the wall is given as:

${\nu }^{\text{'}}=(\frac{v}{v-v_b}$ )  $\nu$ =  $(\frac{v}{v-0.03v}$ )  $\times 40$ =  $\frac{40}{0.97}$ kHz = 41.24 kHz

This frequency is reflected by the stationary wall (  $v_s=0)$ towards the bat

The frequency (  $\nu \text{'}\text{'})\mathrm{o}\mathrm{f}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{}\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{}\mathrm{i}\mathrm{s}\mathrm{}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{}\mathrm{b}\mathrm{y}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:$

${\nu }^{\text{'}\text{'}}=(\frac{v+v_b}{v}$ )  $\nu \text{'}$ = (  $\frac{v+0.03v}{v}$ )  $\times 41.24\mathrm{k}\mathrm{H}\mathrm{z}$ = 1.03  $\times 41.24$ = 42.47 kHz