Work, Energy, and Power Class 11 NCERT Solutions: Download Topic-wise Questions & Answers PDF

• Introduction to Work, Energy, and Power
• Notions of work and kinetic energy: The work-energy theorem
• Work
• Kinetic energy
• Work done by a variable force
• The work-energy theorem for a variable force
• The concept of potential energy
• The conservation of mechanical energy
• The potential energy of a spring
• Various forms of energy: the law of conservation of energy
• Power
• Collisions

Class 11 Chapter 5 Physics NCERT Solutions Work, Energy and Power include important topics like the work-energy theorem, potential energy, the law of conservation of energy etc. The solutions to all the numerical problems are solved here and available in PDF format. The students refer to the PDF to find the answers to all the exercise questions

Download Here: NCERT Solution for Class XI Physics Chapter Work, Energy, and Power PDF

Q.6.1 The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

(b) work done by gravitational force in the above case,

(c) work done by friction on a body sliding down an inclined plane,

(d) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,

(e) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Ans.6.1

• While the person lifts a bucket out of a well by means of a rope tied to the bucket, the direction of both the force and the displacement are same, hence the work done is positive.
• While lifting the bucket, he works against gravity, but the work done by the gravitational force is downward, hence the work done is negative.
• The direction of motion of the object is in the opposite direction of the frictional force; hence the work done is negative.
• While a body moves on a rough horizontal plane, the frictional forces try to oppose the motion. But since the applied force maintains uniform velocity of the object, the motion of the object and the applied force are in the same direction. Hence the work done is positive.
• Since the resistive force of air is trying to bring the vibrating pendulum to rest, the work done is negative.

Q.6.2 A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1.

Compute the

(a) work done by the applied force in 10 s,

(b) work done by friction in 10 s,

(c) work done by the net force on the body in 10 s,

(d) change in kinetic energy of the body in 10 s, and interpret your results.

Ans.6.2

Given, mass of the body, m = 2 kg

Horizontal force applied, F = 7 N

Coefficient of friction,  $\mu$ = 0.1

Acceleration, a = F/m = 7/2 = 3.5 m/s2

Frictional force, f =  $\mu R=\mu mg=$ 0.1  $\times 2\times 9.807=$ 1.96 N

Retardation produced by the frictional force,  $a_r$ = -f/m = -1.96 /2 = 0.98 m/s2

The net acceleration by which the body moves forward

$a_n$ = a -  $a_r$ = 3.5 – 0.98 = 2.52 m/s2

Distance moved by the body in 10 s is given by

s = ut + (1/2)  $a_n{t}^2$ = 0  $\times 10+\left(\frac{1}{2}\right)\times 2.52\times {10}^2$ = 126 m

Work done in 10 s is given by

W = Force  $\times \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}=7\times 126=882\mathrm{J}$

Work done by friction in 10 s is given by

W = -f  $\times s=-1.96\times 126=$ - 247J

Work done by the net force,

W = (F-f)  $\times s$ = (7 – 1.96 )  $\times 126$ = 635 J

Kinetic energy is given by the equation

KE = (1/2)m  $v^2$ where v is the final velocity

From the equation v = u + at we get after 10 s, v = 0 + 2.52  $\times$ 10 = 25.2 m/s

Final kinetic energy = (1/2)  $\times 2\times {25.2}^2$ = 635 J

Initial kinetic energy = (1/2)  $\times 2\times 0^2$ = 0

Change in kinetic energy = 635 – 0 = 635 J

Hence the work done by the net force = change in kinetic energy

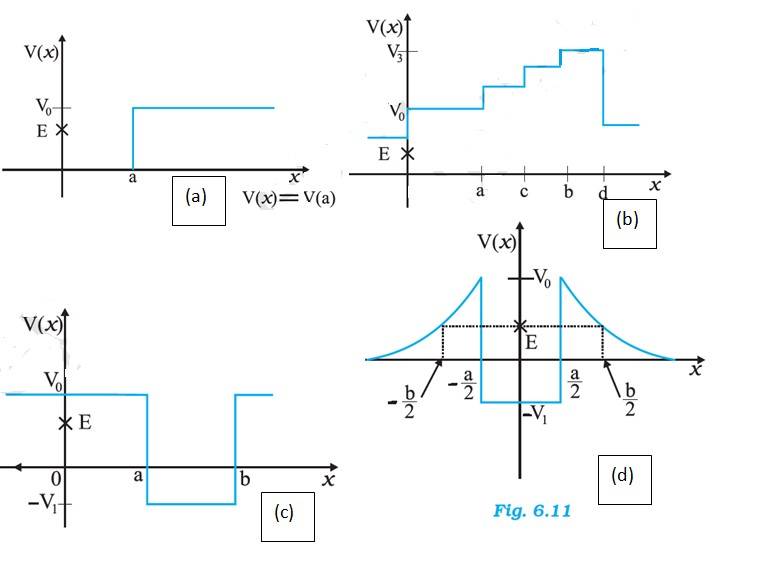
Q.6.3 Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Ans.6.3

We know the total energy E is given by E = Kinetic energy (KE) + Potential energy (PE)

In figure (a), we have at x=0, the potential energy is zero. So KE is positive. At x>a, the potential energy has a value greater than E, so the KE becomes 0. Thus the particle will not exist in the region x>a. Minimum total energy is zero.

For the entire x-axis, PE >E, the KE of the object would be negative. Thus the particle will not exist in this region.

In x=0 to x=a and x>b, PE is greater than E, so he KE has to be negative. The object cannot exist in this region.

For x=-b/2 to x =-a/2 and x=a/2 to x=b/2, KE is positive and the PE

Q.6.4 The potential energy function for a particle executing linear simple harmonic motion is given by V(x) =kx²/2, where k is the force constant of the oscillator. For k = 0.5 N m^-1, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

Ans.6.4

Given, particle energy , E = 1 J,

Force constant, k = 0.5 N/m

Kinetic energy, KE =  $\frac{1}{2}$ mv2

From the equation, total energy, E = KE +PE, we get

1 = (1/2)mv2 + (1/2) kx2

when it turns back, v becomes 0

1 = (1/2)  $\times 0.5\times x^2$ , x = ± 2

Q.6.5 Answer the following :

(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat

energy required for burning obtained? The rocket or the atmosphere?

(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?

(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?

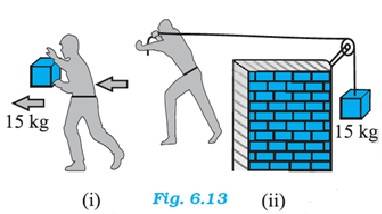
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?

Ans.6.5

As per the law of conservation of energy,

Total energy = potential energy + kinetic energy

= mgh +  $\frac{1}{2}$ mv2

When the casing burns, mass reduces, resulting in drop of energy. Hence the energy for burning of casing is drawn from the rocket.

The force due to gravity is a conservative force. The work done on a closed path for a conservative force is zero. Hence, for every complete orbit of the comet, the work done by the gravitational force is zero.

The potential energy of the satellite revolving the Earth decreases as it approaches the Earth and since the system’s total energy should remain constant, the kinetic energy increases. Hence the satellite velocity increases when it approaches the Earth.

Give, m = 15 kg, displacement, s = 4m

From the relation, work done, W = F  $\times s\times \cos \theta$ where  $\theta$ is the angle between the force and displacement. Here F = mg, hence, W = mgs  $\cos \theta$ = 15  $\times 9.8\times 4\times \cos 90°$ = 0

Mass = 15 kg, s = 4 m, the applied force direction is same as the direction of the displacement,  $\theta =0$ . Hence W = 15  $\times 9.8\times 4\times \cos 0°$ = 588 J

Q,6.6 Underline the correct alternative:

(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.

(c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.

(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

Ans.6.6

When a conservative force does positive work on a body, the body gets displaced in the direction of the force, it moves towards the centre of the force, thus resulting in decrease of potential energy.

When the work done by a body against friction, it reduces its velocity. Hence kinetic energy decreases.

The momentum cannot be changed by the internal forces on the system; the change of momentum is proportional to the external force.

The total linear momentum does not change in an elastic collision.

Q.6.7 State if each of the following statements is true or false. Give reasons for your answer.

(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.

(b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

(c) Work done in the motion of a body over a closed loop is zero for every force in nature.

(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system

Ans.6.7

False. The total momentum and energy is conserved, not the individual.

False. External forces can change the energy of a body.

False. Only work done by conservative force over a closed loop is zero.

True. In an inelastic collision, the final velocity reduces, resulting in loss of the initial kinetic energy.

Q.6.8 Answer carefully, with reasons:

(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?

(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?

(c) What are the answers to (a) and (b) for an inelastic collision?

(d) If the potential energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic?

(Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).

Ans.6.8

In elastic collision, the initial and final kinetic energy is equal. When the two balls collide, there is no conservation of kinetic energy; it gets converted into potential energy.

The total linear momentum is conserved in an elastic collision.

In case of inelastic condition in case (a), there will be loss of kinetic energy but in case of (b), the total linear momentum will be conserved in inelastic collision also.

It is an elastic collision as the forces involves are conservative forces.

Q.6.9 A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to

(i) t ^1/2  (ii) t  (iii) t ^3/2  (iv) t ²

Ans.6.9

Let us assume

Body mass = m

Acceleration = a

According to Newton’s 2nd law F = ma (constant)

We know a = dv/dt = constant. Hence dv = dt  $\times$ constant

On integrating, v = t + constant

The relation of power is given by P = F  $\times v$

We have  $v=u+at$

Hence,  $P=F\times (u+at)$

=  $ma(u+at)$

=  $mau+m{a}^{2}t$

Therefore P  $\propto t$

Q.6.10 A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to

 (i) t ^1/2 

(ii) t 

(iii) t ^3/2

 (iv) t ²

Ans.6.10

Power is given by the relation

P = Fv = mav = mv  $\frac{dv}{dt}$ = constant( say, k)

vdv =  $\frac{k}{m}dt$

$\frac{v^2}{2}=\frac{k}{m}t$

v =  $\sqrt{\frac{2kt}{m}}$

For displacement x of the body, we have:

v =  $\frac{dx}{dt}$ =  $\sqrt{\frac{2k}{m}}{t}^{1/2}$

dx = k’  $t^{1/2}$ dt where k’ =  $\sqrt{\frac{2k}{3}}$ = constant

On integrating both sides, we get

x =  $\frac{2}{3}k\text{'}{t}^{3/2}$

Therefore x  $\alpha t^{3/2}$

Q.6.11 A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by

F = −  $\stackrel{̂}{\mathit{i}}+\mathit{}2\stackrel{̂}{\mathit{j}\mathit{}}$ +3  $\stackrel{̂}{\mathit{k}}$ N

where  $\stackrel{̂}{\mathit{i}\mathit{}}$ ,  $\stackrel{̂}{\mathit{j}}$ ,  $\stackrel{̂}{\mathit{k}}$ are unit vectors along the x-, y- and z-axis of the system respectively.

What is the work done by this force in moving the body a distance of 4 m along the z-axis ?

Ans.6.11:

Force exerted on the body, F = −  $\stackrel{̂}{i}+2\stackrel{̂}{j}$ +3  $\stackrel{̂}{k}$ N

Displacement, s = 4 km

Work done, W = F.s

= (−  $\stackrel{̂}{i}+2\stackrel{̂}{j}$ +3  $\stackrel{̂}{k}).(4\stackrel{̂}{k})$

= 0+0-3  $\times 4$

= 12 J

Q.6.12 An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton ? Obtain the ratio of their speeds. (electron mass = 9.11×10^-31 kg, proton mass = 1.67×10^–27 kg, 1 eV = 1.60 ×10^–19 J).

Ans.6.12

Electron mass, me = 9.11×10-31 kg

Proton mass, mp = 1.67×10–27 kg

Electron’s kinetic energy = 10 keV = 10  $\times$  ${10}^3$  $\times$ 1.60 ×10–19 J = 1.60 ×10–15 J

Proton’s kinetic energy = 100 keV = 100  $\times {10}^3$  $\times$ 1.60 ×10–19 J = 1.60 ×10–14 J

The electron kinetic energy is given by Eke = (1/2)m  $v_e^2$ where  $v_e$ is the velocity of electron

$v_e$ =  $\surd$ {(2  $\times$ Eke )/m} = 5.92  $\times {10}^7$ m/s

The velocity of proton  $v_p$ =  $\surd$ {(2  $\times$ Pke )/m} = 4.37  $\times {10}^6$ m/s

The speed ratio =  $v_e$ /  $v_p$ = 13.5

Q.6.13 A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey ? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10 m s^–1 ?

Ans.6.13

The radius of the rain drop = 2 mm = 2  $\times {10}^{-3}$ m

The height of drop, s = 500 m

Density of water,  $\rho$ =  ${10}^3$ kg/  $m^3$

Mass of the rain drop = volume  $\times density$ = (4/3)  $\pi r^3$  $\times \rho$ = 3.35  $\times {10}^{-5}$ kg

The gravitational force on the raindrop, F = mg = 3.28  $\times {10}^{-4}$ N

Work done by the gravity on the drop is = mgs where s = 250 m

Work done = 0.082 J

The work done during the second half will remain same.

The total energy of the raindrop will be conserved during the motion.

Total energy at the top

E1 = mgh where h = 500 m, E1 = 0.164 J

Due to resistive force, the energy of the drop on reaching the ground

E2 = (1/2)mv² where v = 10 m/s, E2 = 0.001675 J

Work done by the resistive force, W = E1 – E2 = 0.1623 J

Q.6.14 A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?

Ans.6.14

Momentum is always conserved for an elastic or inelastic collision.

The molecule’s initial velocity, u = final velocity v = 200 m/s

Initial kinetic energy = (1/2)m  $u^2$

Final kinetic energy = (1/2)m  $v^2$ = (1/2)m  $u^2$

Therefore, kinetic energy is also conserved

Q.6.15 A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Ans.6.15

Given, the volume of the tank, V = 30  $m^3$

Time required to fill the tank, t = 15 min = 900 s

Height of the tank above the ground, h = 40 m

The efficiency of the pump, ԯ = 30%

The density of water,  $\rho$ =  ${10}^3$ kg/  $m^3$

Now, the mass of the water pumped, m =  $\rho V$ = 30  $\times {10}^3$ kg = 3  $\times {10}^4$ kg

Power consumed = W/t = mgh/t = 3  $\times {10}^4\times 9.8\times$ 40 / 900 = 13066 W

P input = Power consumed / ԯ = 43.6 kW

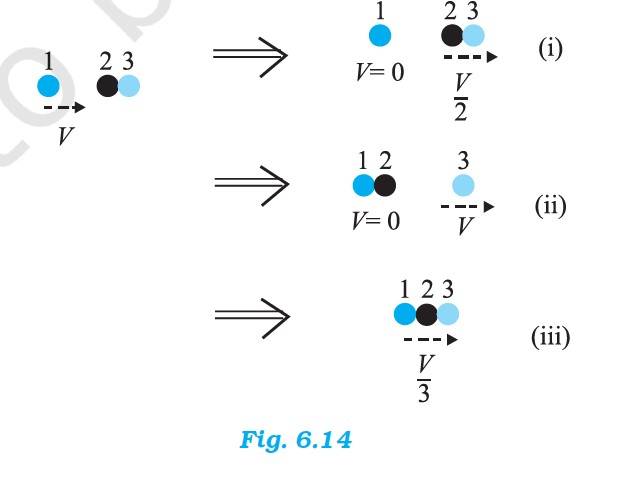
Q.6.16 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig. 6.14) is a possible result after collision ?

Ans.6.16

The mass of the ball bearing = m

Before the collision, the total K.E. of the system = K.E. of the stationary ball bearing + K.E. of the striking ball bearing = 0 +  $\left(\frac{1}{2}\right){mv}^2$

After the collision, the K.E. of the total system is

Case (i) = 0 +  $\left(\frac{1}{2}\right)\left(2m\right){\left(\frac{v}{2}\right)}^2$ =  $\left(\frac{1}{4}\right){mv}^2$

Case (ii) = 0 +  $\left(\frac{1}{2}\right)m{v}^2$

Case(iii) =  $\left(\frac{1}{2}\right)\left(3m\right){\left(\frac{v}{3}\right)/}^2$ =  $\left(\frac{1}{6}\right)m{v}^2$

Case (ii) is possible since K.E. is conserved in this case.

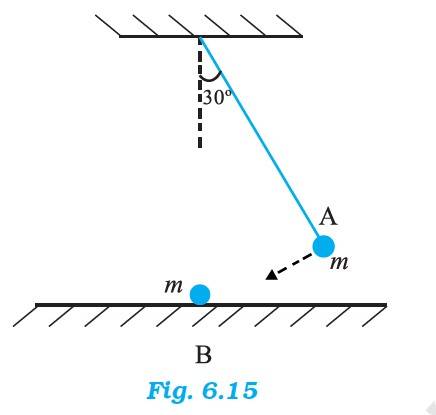
Q.6.17 The bob A of a pendulum released from 30  $°$ to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.

Ans.6.17

In an elastic collision, when the ball A will hit the ball B, A comes to rest immediately and the ball B acquires the velocity of ball A. The momentum thus gets transferred from a moving body to a stationary body.

Q.6.18 The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?

Ans.6.18

The length of the pendulum, l = 1.5 m

The potential energy of the bob at horizontal position = mgl

Since it dissipates 5% of its kinetic energy to come to the horizontal position, from the law of conservation of energy we get,

$\left(\frac{1}{2}\right)m{v}^2$ = (0.95)  $\times mgl$

$v^2$ = 2  $\times 0.95\times 9.81\times 1.5$

v = 5.287 m/s

Q.6.19 A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s–1. What is the speed of the trolley after the entire sand bag is empty?

Ans.6.19

Given, the mass of the trolley,  $m_t$ = 300 kg, mass of the sand bag,  $m_s$ = 25 kg, uniform velocity of the trolley, v = 27 kmph = 0.75 m/s

Since there is no external force acting on the system, the speed of the trolley will remain unchanged even after entire sand is empty. 27 kmph is the answer.

Q.6.20 A body of mass 0.5 kg travels in a straight line with velocity v =a x ^3/2 where a = 5 m^–1/2 s–1. What is the work done by the net force during its displacement from x = 0 to x = 2 m?

Ans.6.20

Mass of the body = 0.5 kg

Velocity, v = a x 3/2

a = 5 m–1/2 s–1

At x =0, the initial velocity, u = 0

At x = 2, the final velocity, v = 5  $\times 2^{3/2}$ = 14.142 m/s

Work done by the system = increase in K.E. of the body = (1/2)m(  $v^2$ -  $u^2$ )

= (1/2)  $\times 0.5\times$ 14.142  $\times 14.142$ = 50 J

Q.6.21 The blades of a windmill sweep out a circle of area A.

(a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t ?

(b) What is the kinetic energy of the air ?

(c) Assume that the windmill converts 25% of the wind’s energy into electrical energy, and that A = 30 m2, v = 36 km/h and the density of air is 1.2 kg m–3. What is the electrical power produced ?

Ans.6.21

Given, the area of the windmill sweep = A, Wind velocity = v

The volume of air passing through the blade = Av

Let the density of air be  $\rho$ , the mass of air passing through the blade =  $\rho Av$

The mass of air passing through the blade in time t =  $\rho Avt$

The kinetic energy of air =  $\left(\frac{1}{2}\right)m{v}^2$ =  $\left(\frac{1}{2}\right)\rho Avt{v}^2$ =  $\left(\rho At{v}^3\right)$ /2 ….(1)

Area, A = 30  $m^2$ , v = 36 km/h = 10 m/s, density of air be  $\rho$ = 1.2 kg/  $m^3$

Total wind energy , from eqn. (1) = 18 kW

Electrical energy = 25 % of wind energy = 0.25  $\times 18=4.5kW$

Q.6.22 A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated.

(a) How much work does she do against the gravitational force ?

(b) Fat supplies 3.8 × 10⁷J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?

Ans.6.22

Mass lifted, m = 10 kg

Height to which the mass lifted, h = 0.5 m

No of repetitions, n = 1000

Work done against gravitational force,

W = nmgh = 1000  $\times 10\times 9.81\times 0.5=$ 49050 J

Mechanical energy supplied by 1 kg fat, with 20% efficiency rate = 0.2  $\times$ 3.8  $\times {10}^7$ = 0.76  $\times {10}^7$ J/kg

Fat used by dieter = 49050 / (0.76  $\times {10}^7)$ kg =  $6.45\times {10}^{-3}$ kg

Q.6.23 A family uses 8 kW of power.

(a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?

(b) Compare this area to that of the roof of a typical house.

Ans.6.23

Power used by the family = 8 kW = 8000 W

Solar energy received = 200 W/  $m^2$

Percentage conversion of Solar energy to Electrical energy = 20%

If the area required is A then 0.2  $\times A\times 200=8000$

A = 200  $m^2$ . The comparable roof size is 14.14 X 14.14 m

Q.6.24 A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.

Ans.6.24

Mass of the bullet,  $m_b$ = 0.012 kg

Initial speed of the bullet, u = 70 m/s

Mass of the wooden block ,  $m_w$ = 0.4 kg

Initial speed of the wooden block = 0

Let’s assume, final speed of the bullet = v

Applying the law of conservation of momentum

$m_b\times u+m_w\times 0=\left(m_b+m_w\right)v$

Hence v = (  $m_b\times u)/\left(m_b+m_w\right)$ = 2.04 m/s

Let h be the height by which the block rise. Applying law of conservation of energy

Potential energy of the combined bullet + block = Kinetic energy of the combination

$\left(m_b+m_w\right)\times g\times h=$ (1/2)  $\times \left(m_b+m_w\right)\times v^2$

h =  $v^2$ /2g = 0.212 m

The heat produced = Initial kinetic energy of the bullet – final kinetic energy of the combination

= (1/2)  $m_b$  $u^2$ - (1/2)  $\times \left(m_b+m_w\right)\times v^2$

= (1/2)  $\times$ 0.012 X  ${70}^2$ - (1/2)  $\times \left(0.012+0.4\right)\times {2.04}^2$ J

= 29.4 – 0.857 J

= 28.54 J

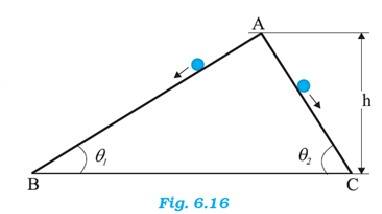
Q.6.25 Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given  ${\mathit{\theta }}_1$ = 30  $°$ ,  ${\mathit{\theta }}_2$ = 60  $°$ , and h = 10 m, what are the speeds and times taken by the two stones ?

Ans.6.25

From the law of conservation of energy,

the potential energy at the top = Kinetic energy at the bottom

mgh = (1/2)m  $v_1^2$ ….(1)

and

mgh = (1/2)m  $v_2^2$ ….(2)

$v_1$ =  $v_2$ , Both the stones will reach with the same speed

For stone 1, the force acting on the stone 1 is given by ,  $F_1$ = m  $\times a_1$ = mg  $\sin {\theta }_1$

$a_1$ = g  $\sin {\theta }_1$

For stone 2,  $a_2$ = g  $\sin {\theta }_2$

As  ${\theta }_2>{\theta }_1$ ,  $a_2$ >  $a_1$

From v = u + at, we get t = v/a

Therefore  $t_2$ <  $t_1$ Stone 2 will reach faster than stone 1

From the law of conservation of energy

mgh = (1/2) mv²

v =  $\sqrt{2gh}$ = 14 m/s ( Given h = 10 m)

The time taken by two stones given as

$t_1$ = v/  $a_1$ = v/g  $\sin {\theta }_1$ = 14/(9.81  $\sin 30°)$ = 2.85 s

$t_2$ = v/  $a_2$ = v/g  $\sin {\theta }_2$ = 14/(9.81  $\sin 60°)$ = 1.65 s

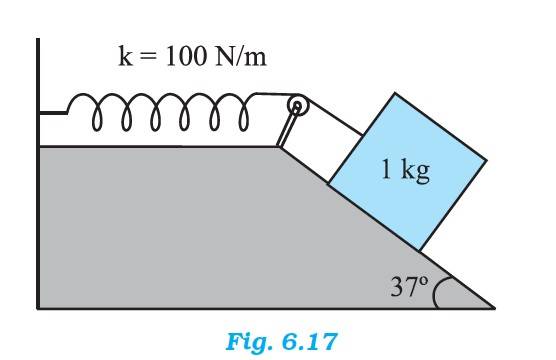
Q.6.26 A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N m^–1 as shown in Fig. 6.17. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest.

Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.

Ans.6.26

Mass of the block = 1 kg

Spring constant = 100 N/m

Displacement of the block, x = 10 cm = 0.1 m

At equilibrium, normal reaction, R =  $mg\cos 37°$

Frictional force, F =  $\mu R$ =  $mg\sin 37°$

Net force acting on the block down on the incline =  $mg\sin 37°$ - F

=  $mg\sin 37°$ -  $\mu mg\cos 37°$

=mg(  $\sin 37°-\mu \cos 37°$ )

At equilibrium,

Work done = Potential energy of the stretched string

mg(  $\sin 37°-\mu \cos 37°$ ) = (1/2)kx2

1 x 10 x (  $\sin 37°-\mu \cos 37°$ ) = (1/2) x 100 x 0.1

10 x (0.602 –  $\mu 0.798)$ = 0.5 x 100 x 0.1

$\mu =0.128$

Q.6.27 A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with an uniform speed of 7 m s^–1. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact ? Would your answer be different if the elevator were stationary ?

Ans.6.27

Mass of the bolt, m = 0.3 kg, Height of the elevator, h = 3 m

Since the bolt did not rebound, the entire potential energy got converted into heat.

The potential energy of the bolt = mgh = 0.3 x 9.8 x 3 J = 8.82 J

The heat produced will remain same even if the lift is stationary, since g = constant

Q.6.28 A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 m s^–1 relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?

Ans.6.28

Mass, m = 200 kg

Speed, v = 36 km/h = 10 m/s

Mass of the boy, M = 20 kg

Initial momentum = (M + m)v = (20 + 200) x 10 kg-m/s = 2200 kg-m/s

If v’ is the final velocity of the trolley, then

The final momentum = (M+m) x v’ – M x 4= 220v’-80

According to the law of conservation of energy,

Initial momentum = final momentum

2200 = 220v’-80

V’ = 10.36 m/s

Time required by the boy to travel 10m = 10/4 = 2.5 s

Distance travel by trolley in 2.5 s = 10.36 x 2.5 m = 25.9 m

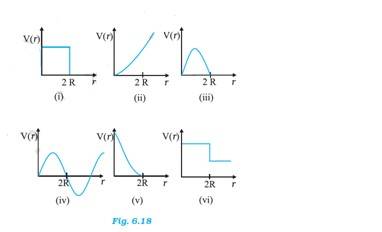
Q.6.29 Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls ? Here r is the distance between centers of the balls.

Ans.6.29

The potential energy of two masses in a system is inversely proportional to the distance between them. The potential energy of the system of two balls will decrease as they get closer to each other. When the balls touch each other, the potential energy becomes zero, I.e. at r = 2R. The potential energy curve in (i),(ii),(iii),(iv) and (vi) do not satisfy these conditions. So there is no elastic collision.

Q.6.30 Consider the decay of a free neutron at rest : n  $\to$ p + e .Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the  $\mathit{\beta }$ -decay of a neutron or a nucleus (Fig. 6.19).

The decay process of free neutron at rest is given as:

n  $\to p+\bar{e}$

From Einstein’s mass-energy relation, we have the energy of electron as Δ  $m{c}^2$ where,

Δm = Mass defect = Mass of neutron – ( Mass of proton + mass of electron)

c = speed of light

Δm and c are constant. Hence, the given two-body decay is unable to explain the continuous energy distribution in the  $\beta$ -decay  $$ of a neutron or a nucleus. The presence of neutrino von the LHS of the decay correctly explain the continuous energy distribution.