NCERT Solutions for Class 12 Physics Chapter 1 - Electric Charges and Fields: Questions and Answers PDF

Q.1.1 What is the force between two small charged spheres having charges of 2 ×  ${10}^{-7}$ C and 3 ×  ${10}^{-7}$ C placed 30 cm apart in air?

Ans.1.1 Charge of the first sphere,  $q_1$ = 2 ×  ${10}^{-7}$ C

Charge of the second sphere,  $q_2$ = 3 ×  ${10}^{-7}$ C

Distance between the spheres, r = 30 cm = 0.3 m

Electrostatic force between the spheres is given by the relation,

F =  $\frac{1}{4\pi {ϵ}_0}$  $\times \frac{q_1{q}_2}{r^2}$ , where  ${ϵ}_0$ = Permittivity of free space = 8.854  $\times {10}^{-12}$  $C^2{N}^{-1}$  $m^{-2}$

Hence, F =  $\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}}$  $\times \frac{2\mathrm{}\times {10}^{-7}\times 3\mathrm{}\times {10}^{-7}}{{\left(0.3\right)}^2}$ = 5.99  $\times {10}^{-3}$ N

Therefore the force between the two small charged spheres is 5.99  $\times {10}^{-3}$ N. The charges are of same nature. Hence, force between them will be repulsive.

 

Q.1.2 The electrostatic force on a small sphere of charge 0.4 μC due to another small sphere of charge –0.8 μC in air is 0.2 N.

(a) What is the distance between the two spheres?

(b) What is the force on the second sphere due to the first?

Ans.1.2 Electrostatic force on the first sphere, F = 0.2 N

Charge on this sphere,  $q_1$ = 0.4 μC = 0.4  $\times {10}^{-6}$ C

Charge on this sphere,  $q_2$ = - 0.8 μC = - 0.8  $\times {10}^{-6}$ C

Electronic force between the spheres is given by the relation

F =  $\frac{1}{4\pi {ϵ}_0}$  $\times \frac{q_1{q}_2}{r^2}$ , where  ${ϵ}_0$ = Permittivity of free space = 8.854  $\times {10}^{-12}$  $C^2{N}^{-1}$  $m^{-2}$

Or  $r^2$ =  $\frac{1}{4\pi {ϵ}_0}$  $\times \frac{q_1{q}_2}{F}$ =  $\frac{1}{4\pi \times 8.854\mathrm{}\times {10}^{-12}}$  $\times \frac{0.4\mathrm{}\times {10}^{-6}\times 0.8\mathrm{}\times {10}^{-6}}{0.2}$ = 0.01438 m2

r = 0.1199 m = 0.12 m

The distance between two spheres is 0.12 m

(b)

Both the spheres attract each other with the same force. Therefore, the force on the second sphere due to the first is also 0.2 N

 

Q.1.3 Check that the ratio ke2/G  ${\mathit{m}}_{\mathit{e}}{\mathit{m}}_{\mathit{p}}$ is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?

Ans.1.3 The units of the given equation $\frac{{ke}^2}{G{m}_e{m}_p}$ is

e = Electric charge in C

k =  $\frac{1}{4\pi {ϵ}_0}$ in N  $m^2{C}^{-2},$ where  ${ϵ}_0$ = Permittivity of free space = 8.854  $\times {10}^{-12}$  $C^2{N}^{-1}$  $m^{-2}$

G = Gravitational constant = N  $$

$m^2{kg}^{-2}$

${\mathrm{m}}_{\mathrm{e}}=\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{}\mathrm{k}\mathrm{g},\mathrm{}\mathrm{}{\mathrm{m}}_{\mathrm{p}}=\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{}\mathrm{k}\mathrm{g}$

Therefore

$\frac{{ke}^2}{G{m}_e{m}_p}$ =  $\frac{\left[\mathrm{N}{m}^2{C}^{-2}\right]\times \left[C^2\right]}{\left[\mathrm{N}{m}^2{kg}^{-2}\right]\left[kg\right]\left[kg\right]}$= $M^0{L}^0{T}^0$

So the given equation is dimensionless

We have the following values

e = 1.6 $\times {10}^{-19}$ C

G = 6.67   $\times {10}^{-11}$ ${\mathrm{Nm}}^2{kg}^{-2}$ kg

${\mathrm{m}}_{\mathrm{e}}=9.1\times {10}^{-31}$ kg

${\mathrm{m}}_{\mathrm{p}}=1.66\times {10}^{-27}$

The numerical value of this ratio is given by

$\frac{{ke}^2}{G{m}_e{m}_p}$ =  $\frac{\left[\mathrm{N}{m}^2{C}^{-2}\right]\times \left[C^2\right]}{\left[\mathrm{N}{m}^2{kg}^{-2}\right]\left[kg\right]\left[kg\right]}$ =  $\frac{1}{4\pi {ϵ}_0}$ =  $\times \frac{e^2}{G{m}_e{m}_p}$= 
$\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}}$ $\times \frac{{(1.6\mathrm{}\times {10}^{-19})}^2}{6.67\times {10}^{-11}\times {9.1\times {10}^{-31}\times 1.66\times {10}^{-27}}_{}}$

 = 2.284 $\times {10}^{39}$

 

Q.1.4 (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.

(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?

Ans.1.4 Electric charge of a body is quantized, this means that only integers (1,2,3,….n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integers.

In macroscopic i.e. large scale charges, the charges used are huge as compared to the electric charge of electrons or protons. Therefore, it is ignored and it is considered that electric charge is continuous.

 

Q.1.5 When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.

Ans.1.5 When two bodies are rubbed against each other, it produces charges of equal magnitude in both the bodies but of opposite in nature. Hence the net charges of the two bodies are zero. When a glass rod is rubbed with a silk cloth, similar phenomena occur. This is as per the law of conservation of energy.

 

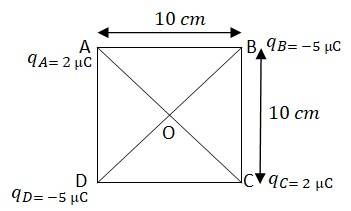
Q.1.6 Four point charges ${\mathit{q}}_{\mathit{A}}$ = 2 μC,  ${\mathit{q}}_{\mathit{B}}$ = –5 μC,  ${\mathit{q}}_{\mathit{C}}$= 2 μC, and ${\mathit{q}}_{\mathit{D}}$ = –5 μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 μC placed at the centre of the square?

Ans.1.6

 

In the adjoining figure ABCD is a square with sides AB = BC = CD = DA = 10 cm

Diagonals, AC = BD  =  $\sqrt[]{{10}^2+{10}^2}$ = $10\sqrt[]{2}$cm

AO = OC = DO = BO = $5\sqrt[]{2}$ cm

At the centre of the square ABCD, O, a charge of 1 $\mu Cisplaced.$ $\text{exception 25:}$

The force of repulsion between the charges placed at A and at O is equal in magnitude but opposite in direction between the charges placed at point C and centre O. Similarly the force of attraction between the charges placed at B & O and D & O will be equal in magnitude but opposite in direction. These charges will cancel each other.

Hence, the net charge at centre O will be zero.

 

Q.1.7 (a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?

(b) Explain why two field lines never cross each other at any point?

Ans.1.7 An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to another.

The electric field intensity will show two directions at that point where two filed lines crosses. This is not possible. Hence they do not cross.

 

Q.1.8 Two point charges ${\mathit{q}}_{\mathit{A}}$= 3 μC and ${\mathit{q}}_{\mathit{B}}$= –3 μC are located 20 cm apart in vacuum.

(a) What is the electric field at the midpoint O of the line AB joining the two charges?

(b) If a negative test charge of magnitude 1.5 $\times {10}^{-9}$  C is placed at this point, what is the force experienced by the test charge?

Ans.1.8 The situation is represented in the following figure.

O is the midpoint of AB, hence OA = OB = 10 cm = 10 $\times {10}^{-2}$ $m^2$

The electric field at O caused by the charge at A is given by

 

  $E_1$ = $\left|\frac{4\pi {ϵ}_0}{}\mathrm{}\times \frac{q_A}{r^2}\right|$ along OB and the electric field at O caused by the charge at B is given by,

  $E_2$ = $\left|\frac{1}{4\pi {ϵ}_0}\mathrm{}\times \frac{q_B}{r^2}\right|$along OB

where ${ϵ}_0$= Permittivity of free space = 8.854 $\times {10}^{-12}$ $<br>$  $C^2{N}^{-1}$ $m^{-2}$

Net electric field at point O, E = $E_1+E_2$ = $\frac{1}{4\pi {ϵ}_0{r}^2}$ $\times \left|q_A\mathrm{}+\mathrm{}{q}_B\right|$

$\left|{}_{}\right|$  $\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}{\times (10\mathrm{}\times {10}^{-2})}^2}$ $\times \left|3\times {10}^{-6}\mathrm{}+\mathrm{}3\times {10}^{-6}\right|$ 

=5.39 $\times {10}^6$ N $C^{-1}$ along OB

A test charge of amount 1.5 $\times {10}^{-9}$  C is placed at the midpoint O

So the force experienced by the test charge, F = q $\times E$ $<br>$

= 1.5   5.39 $\times {10}^6$  $<br>$ N = 8.088 $\times {10}^{-3}$ $<br>$ N

This force is directed along the line OA, this is because the negative test charge is repelled by the charge placed at point B but attracted towards point A.

 

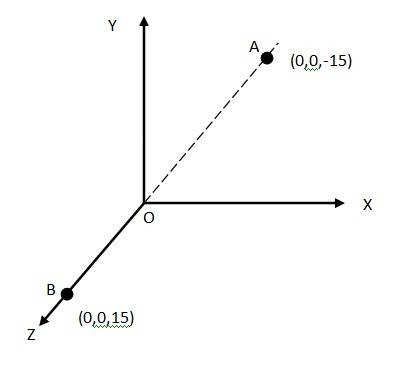
Q.1.9 A system has two charges ${\mathit{q}}_{\mathit{A}}$  = 2.5 $\times {10}^{-7}$ ${\mathit{<br>}}_{}$ C and  $<math>\; <msub>\; <mrow>\; <mrow>\; <mi\; mathvariant="bold-italic">\; q\; </mi>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mi\; mathvariant="bold-italic">\; B\; </mi>\; </mrow>\; </mrow>\; </msub>\; </math>$ = –2.5 $\times {10}^{-7}$ ${\mathit{<br>}}_{}$ C located at points A: (0, 0, –15 cm) and B: (0,0, +15 cm), respectively. What are the total charge and electric dipole moment of the system?

Ans.1.9

At A, the amount of charge, $q_A$2.5 $\times {10}^{-7}$ C

At B, the amount of charge, $q_B$ $<br>$ = –2.5 $\times {10}^{-7}$ C

Total charge of the system, q = $q_A$ ${\mathrm{<br>}}^{}$ + $q_B$ = 0

Distance between two charges at point A and B = 15 + 15 = 30 cm = 0.3 m

Electric dipole moment of the system is given by p  = $q_A\times d$ =  $q_B\times d$ = 2.5 $\times {10}^{-7}\times 0.3$= 7.5 $\times {10}^{-8}$  C m, along positive z axis.

Q.1.10 An electric dipole with dipole moment 4  $\times {10}^{-9\mathrm{<br>}}$ C m is aligned at 30° with the direction of a uniform electric field of magnitude 5  $\times {10}^4$ N $C^{-1}$ . Calculate the magnitude of the torque acting on the dipole.

Ans.1.10 Electric dipole moment, p = 4  ${\mathit{10}}^{-9\mathrm{<br>}}$ C m

Angle made by p with a uniform electric field,  $\theta$ = 30 $°$

Electric field, E = 5  $\times {10}^4$N $C^{-1}$

Torque acting on the dipole is given by $\tau$= pE $\sin \theta$ = 4 $\times {10}^{-9}\times$ 5 $\times {10}^4\times \sin 30°$

= 1 $\times {10}^{-4}$ Nm

Therefore, the magnitude of the torque acting on the dipole is ${10}^{-4}$ Nm

Q.1.11 A polythene piece rubbed with wool is found to have a negative charge of 3  ${10}^{-7\mathrm{<br>}}$ C.

(a) Estimate the number of electrons transferred (from which to which?)

(b) Is there a transfer of mass from wool to polythene?

Ans.1.11 When polythene rubbed against wool, a number of electrons get transferred from wool to polythene. Hence, wool becomes positively charged and polythene negatively charged.

Amount of charge on the polythene piece, q = -3  $\times {10}^{-7}$ C.

Amount of charge of 1 electron e = -1.6  $\times {10}^{-19\mathrm{<br>}}$

So number of electron transferred from wool to polythene

= ${\mathrm{<br>}}^{}$- $\frac{3\mathrm{}\times {10}^{-7}}{-1.6\mathrm{}\times {10}^{-19}}$1.875 $\times {10}^{12}$

Since electron has a mass, so there will be transfer of mass also.

Mass of single electron ,  $<math>\; <msub>\; <mrow>\; <mrow>\; <mi>\; m\; </mi>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mi>\; e\; </mi>\; </mrow>\; </mrow>\; </msub>\; </math>$ = 9.1 $\times {10}^{-31}$ kg

Total mass transferred from wool to polythene = 1.875 $\times {10}^{12}\times$9.1 $\times {10}^{-31}$ kg

= 1.706 $\times {10}^{-18}$kg $\approx$ negligible

Hence a negligible amount of mass is transferred from wool to polythene.

 

Q.1.12 (a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 $\times {10}^{-7}$ C? The radii of A and B are negligible compared to the distance of separation.

(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?

Ans.1.12 Charge on sphere A, $q_A$ = 6.5 $\times {10}^{-7}$ C

Charge on sphere B, $q_B$ = 6.5 $\times {10}^{-7}$ C

Distance between the spheres, r = 50 cm = 0.5 m

Force of repulsion between two spheres

F =  $\frac{1}{4\pi {ϵ}_0}$ $\times \frac{q_1{q}_2}{r^2}$ , where ${ϵ}_0$= Permittivity of free space = 8.854 $\times {10}^{-12}$  ${\mathrm{<br>}}_{}$   $C^2{N}^{-1}$ $m^{-2}$Therefore, F =   $\frac{1}{4\times \pi \times {8.854\mathrm{}\times {10}^{-12}}_{}}$ $\times \frac{6.5\mathrm{}\times {10}^{-7}\times 6.5\mathrm{}\times {10}^{-7}}{{0.5}^2}$N = 0.0152 N = 1.52  $\times {10}^{-2}$N

Charge on sphere A, $q_A$ = 2 $\times$6.5   $\times {10}^{-7}$C = 1.3

Charge on sphere B, $q_B$ = 2 $\times$ 6.5 $\times {10}^{-7}$C = 1.3 $<br>$

Distance between the spheres, r = $\mathrm{<br>}$ $\frac{50}{2}$ = 25 cm = 0.25 m

Force of repulsion between two spheres

F =   $\frac{1}{4\pi {ϵ}_0}$ $\times \frac{q_1{q}_2}{r^2}$, where ${ϵ}_0$ = Permittivity of free space = 8.854   $\times {10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$Therefore, F =  ${\mathrm{<br>}}^{}$  $\frac{1}{4\times \pi \times {8.854\mathrm{}\times {10}^{-12}}_{}}$ $\times \frac{1.3\mathrm{}\times {10}^{-6}\times 1.3\mathrm{}\times {10}^{-6}}{{0.25}^2}$N = 0.243 N

 

Q.1.13 Suppose the spheres A and B in Exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?

Ans.1.13 When the third uncharged sphere C is brought in contact with the sphere A, then the charge is shared and becomes half. Then

  $q_A$ = $\frac{q}{2}$and  =  $q_C$= $\frac{q}{2}$

When the charged sphere C is brought in contact with charged sphere B, the charge between both the sphere is shared and becomes half

  $q_B,q_C=\frac{1}{2}$ (q + =  $\frac{q}{2})$ $\frac{3q}{4}$ 

Hence the force of repulsion between sphere A and B can be given as

F =  $\frac{\mathrm{<br>1}}{4\pi {ϵ}_0}$ $\times \frac{q_1{q}_2}{r^2}$, where ${ϵ}_0$  = Permittivity of free space = 8.854   $\times {10}^{-12}$  $C^2{N}^{-\mathrm{1 \; \; }}$ $m^{-2}$ = = $\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}}$ =  $\times \frac{(\frac{q}{2}\times \frac{3q}{4})}{{0.5}^2}$ = $\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}}$ $\times \frac{3\times q^2}{{8\times 0.5}^2}$ 
= $\frac{1}{4\times \pi \times 8.854\mathrm{}\times {10}^{-12}}$ $\times \frac{3\times {(6.5\mathrm{}\times {10}^{-7})}^2}{{8\times 0.5}^2}$  = 5.695 $\times {10}^{-3}$N

 

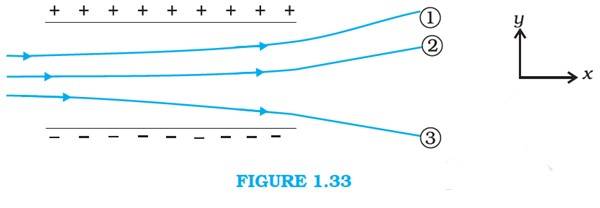
Q.1.14 Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

 

Ans.1.14 Since the charges 1 & 2 are attracted towards + ve, their charges will be – ve. The charge 3 is attracted towards – ve, hence its charge will be +ve.

The charge to mass ratio (emf) is directly proportional to the displacement, charge 3 will have the highest charge to mass ratio.

 

Q.1.15 Consider a uniform electric field E = 3 $\times {10}^3$ î N/C.

(a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?

(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?

Ans.1.15 Electric field intensity, E = 3 $\times {10}^3$ î N/C

Magnitude of electric field intensity, $\left|E\right|$ $=3\times {10}^3$ =  $\left|\mathrm{<br>}\right|$ N/C

Side of the square, s = 10 cm = 0.1 m

Area of the square, A =  $s^2$ = 0.01 $m^2$

The plane of the square is parallel to the y-z plane, hence the angle between the unit vector normal to the plane and electric field, $\theta$= 0 $°$ $\mathrm{<br>}$

Flux ( $\phi )$ through the plane is given by the relation,   $\phi$ =  $\left|E\right|A\cos \theta$ =  $3\mathrm{}\times {10}^3\times 0.01\times \cos 0°=30$
${\mathrm{Nm}}^2/$C

When the normal to its plane make a 60 $°$ angle with x-axis, $\theta$  = 60  $\mathrm{<br>}$ . From the equation  $\phi$ = $\left|E\right|A\cos \theta$we get  =  $\phi$ $3\mathrm{}\times {10}^3\times 0.01\times \cos 60°=15$ ${\mathrm{Nm}}^2/$C

 

Q.1.16 What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?

Ans.1.16 When the cube side is oriented so that its faces are parallel to the coordinate planes, number of field lines entering the cube is equal to the number of field lines piercing out of the cube. A as a result, net flux through the cube is zero.

 

Q.1.17 Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 ×  $<br>$  ${10}^3\mathit{}$ ${\mathrm{Nm}}^2/$C.

(a) What is the net charge inside the box?

(b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?

Ans.1.17 Net outward flux through the surface of the box ,  $\phi$ = 8.0 ×  ${10}^3$ ${\mathrm{Nm}}^2/$C

For a body containing net charge q, flux is given by the relation,  ${\mathrm{<br>}}^{}$  $\phi$ = $\frac{q}{{ϵ}_0}$ 

where ${ϵ}_0$= Permittivity of free space = 8.854  ${\mathrm{<br>}}_{}$  $\times {10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

Hence q =   $\phi$ $\times {ϵ}_0$= 8.0 × ${10}^3\times$ 8.854 $\times {10}^{-12}$ C = 7.0832 $\times {10}^{-8}$ C

= 7.0832 $\times {10}^{-2}\mu C$

Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that the net charge inside the body is zero. The body may have equal amount of positive and negative charges.

 

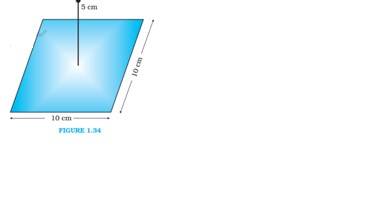
Q.1.18 A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)

 

Ans.1.18 The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed.

According to Gauss’s theorem for a cube, total electric flux is through all its six faces.

  ${\phi }_{Tota\mathrm{l\; =}}$ $\frac{q}{{ϵ}_0}$ 

$\mathrm{H}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e},\mathrm{}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{}\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{g}\mathrm{h}\mathrm{}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{c}\mathrm{u}\mathrm{b}\mathrm{e}$ i.e. through the square is $\phi =\frac{{\phi }_{Total}}{6}$ =  $\frac{q}{{6ϵ}_0}$ ,Where ${ϵ}_0$= Permittivity of free space = 8.854 ${\mathrm{<br>}}_{}$  $\times {10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

We have q = +10 $\mu C$

Hence,  =  $\phi$ =  $\frac{q}{{6ϵ}_0}$ = $\frac{10\times {10}^{-6}}{6\times 8.854\mathrm{}\times {10}^{-12}}$= 188238.83 N $m^2{C}^{-1}$  = 1.88 $\times {10}^5$ N $m^2{C}^{-1}$   $<br>$

 

Q.1.19 A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?

Ans.1.19 Net electric flux ( ${\phi }_{Net}$ ) through the cubic surface is given by

${\phi }_{Net}$ = $\frac{q}{{ϵ}_0}$

where ${ϵ}_0$ = Permittivity of free space = 8.854 × ${10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

q= 2.0 μC

${\phi }_{Net}$ = $\frac{2\times {10}^{-6}}{8.854\mathrm{}\times {10}^{-12}}$  $C^{-1}N$  $m^2=2.25\times {10}^5$ 

 

Q.1.20 A point charge causes an electric flux of –1.0   $\times {10}^3$ N ${\mathit{m}}^2$/C to pass through a spherical Gaussian surface of 10.0 cm radius centered on the charge.

(a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?

(b) What is the value of the point charge?

Ans.1.20 Electric flux, $\phi$= –1.0 $\times {10}^3$ N $m^2$/C

Radius of Gaussian surface, r = 10 cm = 0.1 m

Electric flux piercing through a surface depends on the net charge enclosed inside a body, not on the size of the body. Hence, if the radius is doubled, the net flux passing does not change. The net flux passing will remain as -1  N $\times {10}^3$ N $m^2$/C

The relation between point charge and the electric flux is given by $\phi$= $\frac{q}{{ϵ}_0},$

Where ${ϵ}_0$= Permittivity of free space = 8.854 × ${10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

Hence point charge q = φ $\times$ ${ϵ}_0$= –1.0 $\times {10}^3\times$ 8.854 $\times {10}^{-12}$ C = - 8.854 $\times {10}^{-9}$ C

= - 8.854 $\times {10}^{-3}\mu$C

 

Q.1.21 A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 $\times {10}^3$ N/C and points radially inward, what is the net charge on the sphere?

Ans.1.21 Electric field intensity, E, at a distance d, from the centre of a sphere containing net charge q is given by the relation,

E =   $\frac{1}{4\pi {ϵ}_0}$ $\times \frac{q}{d^2}$

Where ${ϵ}_0$= Permittivity of free space = 8.854 × ${10}^{-12}$  $C^2{N}^{-1}$ $m^{-2},$

q= Net charge

E = 1.5 $\times {10}^3$ N/C

d = 2r = 20 cm = 0.2 m

q = E $4\pi {ϵ}_0\times d^2$ ${}^{}$ = 1.5 $\times {10}^3\times 4\times \pi \times$ 8.854 $\times {10}^{-12}\times {0.2}^2$ C = 6.67 × ${10}^{-9}$C

= 6.67 nC

The net charge on the sphere is 6.67 nC

 

Q.1.22 A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/ ${\mathit{m}}^2$  .

(a) Find the charge on the sphere.

(b) What is the total electric flux leaving the surface of the sphere?

Ans.1.22 Diameter of the sphere, d = 2.4 m, Radius, r = 1.2 m

Surface charge density,   = 80 μC/ $m^2$  = 80 $\times {10}^{-6}$  C/ $m^2$

Total charge on the surface of the sphere is given by Q =   A, where A = surface area of the sphere = 4 $\pi r^2$ $\mathrm{<br>}$

Hence Q = 80 $\times {10}^{-6}\times 4\times \pi \times {1.2}^2$ C = 1.447 $\times {10}^{-3}$ C

The total electric flux (  $<math>\; <msub>\; <mrow>\; <mrow>\; <mi>\; \phi \; </mi>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mi>\; T\; </mi>\; <mi>\; o\; </mi>\; <mi>\; t\; </mi>\; <mi>\; a\; </mi>\; <mi>\; l\; </mi>\; </mrow>\; </mrow>\; </msub>\; </math>$ ) is given by  ${\phi }_{Total}$ = $\frac{Q}{{ϵ}_0},$

where ${ϵ}_0$ = Permittivity of free space = 8.854 $\times {10}^{-12}$ $C^2{N}^{-1}$ $m^{-2}$,

Q = 1.447 $\times {10}^{-3}$ C

$<math>\; <msub>\; <mrow>\; <mrow>\; <mi>\; \phi \; </mi>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mi>\; T\; </mi>\; <mi>\; o\; </mi>\; <mi>\; t\; </mi>\; <mi>\; a\; </mi>\; <mi>\; l\; </mi>\; </mrow>\; </mrow>\; </msub>\; </math>$ =  ${\mathrm{<br>}}_{}$  $\frac{1.447\mathrm{}\times {10}^{-3}}{8.854\mathrm{}\times {10}^{-12}}$  $C^{-1}N$ $m^2$= 1.63   $\times {10}^8$  $C^{-1}N$ $m^2$

 

Q.1.23 An infinite line charge produces a field of 9 $\times {10}^4$ N/C at a distance of 2 cm. Calculate the linear charge density.

Ans.1.23 Electric field produced by the infinite line charge at a distance d having linear charge density $\lambda$  $<br>\mathit{}$ is given by

E = $\frac{\lambda }{2\pi {\epsilon }_{0}d}$, where

E = Electric field = 9 $\times {10}^4$ N/C

$<br>$ ${ϵ}_0$ = Permittivity of free space = 8.854   $\times {10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

d = 2 cm = 0.02 m

Hence, $\lambda$ = 9   $\times {10}^4$ $\times 2\times \pi \times$8.854 $\times {10}^{-12}\times$ $<br>$ 0.02 = 10 $\mu C/m$  $<br>$

 

Q.1.24 Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0   $\times {10}^{-22}\mathit{}$ C/ ${\mathit{m}}^2$. What is E:

(a) in the outer region of the first plate,

(b) in the outer region of the second plate, and

(c) between the plates?

Ans.1.24 The given conditions are explained in the adjacent diagram

 

Where A and B represent two large, thin metal plates, parallel and close to each other. The outer surface of A is shown as I, outer surface of B is shown as II and the surface in between A and B is shown as III.

Charge density of plate A, $\sigma$ = 17.0 $\times {10}^{-22}$C/ $m^2$

Charge density of plate B, $\sigma$ = $-$ 17.0 $\times {10}^{-22}$ $<br>$ C/ $m^2$ $$

& (b) In the region, I and III, electric field E is zero, because charge is not enclosed by the respective plates.

(c) Electric field, E in the region II is given by

E = $\frac{\sigma }{{ϵ}_0}$ ${\mathrm{<br>}}^{}$ , where

$\frac{\mathrm{<br>}}{}$ ${ϵ}_0$ = Permittivity of free space = 8.854   $\times {10}^{-12}$  $C^2{N}^{-1}$ $m^{-2}$

E = $\frac{17.0\mathrm{}\times {10}^{-22}}{8.854\mathrm{}\times {10}^{-12}}$ N/C = 1.92 $\times {10}^{-10}$  N/C

 

Q.1.25 An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 $\times {10}^4\mathit{}\mathit{N}{\mathit{C}}^{-1}$ (Millikan’s oil drop experiment). The density of the oil is 1.26 g / ${\mathit{c}\mathit{m}}^3$  . Estimate the radius of the drop.

(g = 9.81 m/ ${\mathit{s}}^2$ ; e = 1.60 $\times {10}^{-19}$ C).

Ans.1.25 Excess electrons on an oil drop, n = 12

Electric field intensity, E = 2.55 $\times {10}^{4}N{C}^{-1}$ $\mathit{}$

Density of oil, $\rho =$ 1.26 g / ${cm}^3$ $$ = 1.26 $\times {10}^3$  g/ $m^3$

Acceleration due to gravity, g = 9.81 m/ $s^2$  ${\mathrm{<br>}}^{}$

Charge of an electron, e = 1.60 $\times {10}^{-19}$C

Let the radius of the oil drop be r

Force (F) due to electric field (E) is equal to the weight of the oil drop (W)

F = W

Eq = mg

Ene = $\frac{4}{3}\pi r^3\times \rho \times g$

$$ $r^3$ =  $\frac{3\times E\times n\times e}{4\times \pi \times \rho \times g}$= $\frac{3\times 2.55\mathrm{}\times {10}^4\times 12\times 1.60\mathrm{}\times {10}^{-19}}{4\times \pi \times 1.26\times {10}^3\times 9.81}$

r = 9.815 $\times {10}^{-7}$ m = 9.815 $\times {10}^{-4}$ mm

 

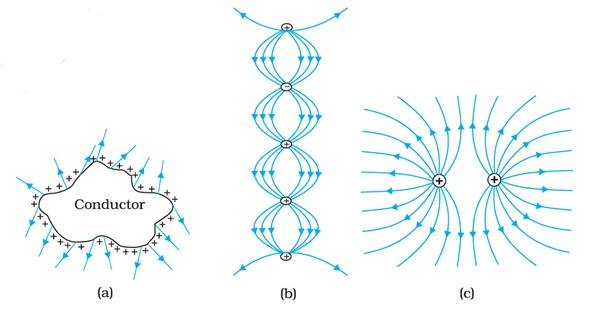
Q.1.26 Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?

 

 

Ans.1.26 The field lines showed in (a) do not represent electrostatic field lines because field lines must be normal to the surface of the conductor.

The field lines shown in (b) do not represent electrostatic field lines because field lines can not emerge from a negative charge and cannot terminate at a positive charge.

The field lines shown in (c) represent electrostatic field line. This is because the field lines emerge from the positive charge and repel each other.

The field lines shown in (d) do not represent electrostatic field lines because the field lines should not intersect each other.

The field lines shown in (e) do not represent electrostatic field lines because closed loops are not formed in the area between the field lines.

 

Q.1.27 In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of   ${10}^5$ N ${\mathit{C}}^{-1}$per meter. What are the force and torque experienced by a system having a total dipole moment equal to ${10}^{-7}$  Cm in the negative z-direction?

Ans.1.27 Dipole moment of the system, p = q $\times dl$ = ${10}^{-7}$ Cm

Rate of increase of electric field per unit length, $\frac{dE}{dl}$ = ${10}^5$ N $C^{-1}$  ${\mathrm{<br>}}^{}$

Force experienced by the system is given by the relation, F = qE = q $\times \frac{dE}{dl}\times dl$  ${\mathrm{<br>}}^{}$

= (q   $\times dl)\times \frac{dE}{dl}$ =p  $\times \frac{dE}{dl}$ = $-{10}^{-7}\times$ ${10}^5$= ${-10}^{-2}$ N

The force is  N in the negative z-direction i.e. opposite to the direction of electric field. Hence, the angle between electric field and dipole moment is 180 $°$ ${\mathrm{<br>}}^{}$.

Torque ( $\tau$ ) is given by the relation, $\tau$ = pE $\sin 180°$ = 0

Therefore, the torque experienced by the system is zero.

 

Q.1.28 (a) A conductor A with a cavity as shown in Fig. 1.36(a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.

(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q + q [Fig. 1.36(b)].

(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.

 

Ans.1.28 Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.

Let q be the charge inside the conductor and ${ϵ}_0$ the permittivity of free space.

According to Gauss’s law, Flux, $\phi$  = E.ds = $\frac{q}{{ϵ}_0}$

Here, E = 0, hence $\frac{q}{{ϵ}_0}$ = 0, so q = 0 (as ${ϵ}_0\ne 0)$

Therefore, the charge inside the conductor is zero. The entire charge Q appears on the outer surface of the conductor.

The outer surface of the conductor A has a charge amount Q. Another conductor B, having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount –q will be induced in the inner surface of the conductor A and +q is induced on the outer surface of conductor A. Therefore, total charge on the outer surface of the conductor A is Q+q.

A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.

 

Q.1.29 A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is ( $\frac{\mathit{\sigma }}{2{\mathit{\epsilon }}_0}$  )  , where  $\stackrel{̂}{\mathit{n}}$ is the unit vector in the outward normal direction, and $\mathit{\sigma }\mathit{}$ is the surface charge density near the hole.

Ans.1.29 Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero. Let E be the electric field outside the conductor, q is the electric charge, $\sigma$is the charge density and ${\epsilon }_0$ is the permittivity of free space.

Charge q = $\sigma$ $\times ds$ 

According to Gauss’s law, flux $\phi$ = E.ds =  $\frac{q}{{ϵ}_0}$= $\frac{\sigma \mathrm{}\times ds}{{ϵ}_0}$

Hence, E = $\frac{\sigma }{2{\epsilon }_0}\stackrel{}{n}$

Therefore, the electric field just outside the conductor is $\frac{\sigma }{{2\epsilon }_0}\stackrel{}{n}$ . This field is a superposition of field due to the cavity E’ and the field due to the rest of the charged conductor E’. These fields are equal and opposite inside the conductor and equal in magnitude and direction outside the conductor.

So E’ + E’ = E

E’  = $\frac{E}{2}$= $\frac{\sigma }{2{\epsilon }_0}\stackrel{}{n}$

Hence, the field due to the rest of the conductor is $\frac{\sigma }{2{\epsilon }_0}\stackrel{}{n}$ $\frac{\mathrm{<br>}}{}\stackrel{}{̂}$

 

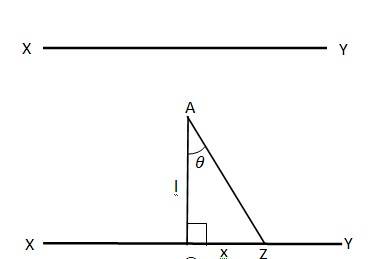
Q. 1.30 Obtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using Gauss’s law.

[Hint: Use Coulomb’s law directly and evaluate the necessary integral.]

Ans.1.30

 

Take a long thin wire XY of uniform linear charge density $\lambda$. Consider a point A at a perpendicular distance l from the midpoint O of the wire. Let E be the electric field at point A due to the wire XY. Consider a small length element dx on the wire section with OZ = x. Let q be the charge on this piece.

Q = $\lambda dx$

Electric field due to the piece,

dE =  =  $\frac{1}{4\pi {\epsilon }_0}\times \frac{\lambda dx}{{\left(AZ\right)}^2}$  = $\frac{1}{4\pi {\epsilon }_0}\times \frac{\lambda dx}{(l^2+x^2)}$since AZ = $\text{exception 25:}$

The electric field is resolved into two rectangular components. dE $\cos \theta$ is the perpendicular component and dE $\sin \theta$ $$ When the whole wire is considered, the component dE  $\sin \theta \mathrm{}\mathrm{i}\mathrm{s}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}.\mathrm{}$ is cancelled. Only the perpendicular component dE $\cos \theta$ affects point A.

Hence, effective electric field at point A due to element dx is $d{E}_1$  $\mathrm{<br>}$

 …………………..(1)

In  ,  $∆AZO$ ,   $\tan \theta =\frac{x}{l}$ ,x = $l\tan \theta$………..(2)

On differentiating equation (2), we get

$\frac{dx}{d\theta }=l{sec}^2\theta$ , dx = …………….(3)

From equation (2), we have

  $x^2$ + $l^2$ =  $l^2{tan}^2\theta +l^2$ = $l^2{sec}^2\theta$…….(4)

Putting equations (3) and (4) in equation (1), we get

  $d{E}_1=\frac{1}{4\pi {\epsilon }_0}\times \frac{\lambda l{sec}^2\theta d\theta \cos \theta }{l^2{sec}^2\theta }$ = $\frac{1}{4\pi {\epsilon }_0}\times \frac{\lambda \cos \theta d\theta }{l}$……..(5)

The wire is so long that $\theta$tends from   $-\frac{\pi }{2}$to $\frac{\pi }{2}$

By integrating equation (5), we get

  ${\int }_{-\frac{\pi }{2}}^{\mathrm{}\frac{\pi }{2}}d{E}_{\mathrm{1=}}$ ${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}(\frac{1}{4\pi {\epsilon }_0}\times \frac{\lambda \cos \theta d\theta }{l})$

$E_1=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda }{l}{\left[\sin \theta \right]}_{\mathrm{}-\frac{\pi }{2}}^{\frac{\pi }{2}}$

$E_1=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda }{l}\times 2=\frac{\lambda }{2\pi {\epsilon }_{0}l}$

Therefore the electric field due to long wire is $\frac{\lambda }{2\pi {\epsilon }_{0}l}$

 

Q.1.31 It is now established that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge + (2/3) e, and the ‘down’ quark (denoted by d) of charge (–1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.

Ans.1.31 A proton has 3 quarks. Let there be n ‘up quarks’, then number of ‘down quarks’ = 3-n

Charge due to n ‘up quarks’ = $(\frac{2}{3}$ e) n

Charge due to (3-n) ‘down quarks’ = $-$ $\frac{1}{3}e\left)\right(3-n)$ 

Total charge on a proton = +e = $(\frac{2}{3}$ e) n +  ( - $\frac{1}{3}e\left)\right(3-n)$  $<br>$

e =  $\frac{2ne}{3}$ + $\frac{ne}{3}$-e

2e = $\frac{3ne}{3}$

n = 2

Number of ‘up quark’ = 2 and number of ‘down quark’ = 1. Therefore a proton can be represented as ‘uud’.

A neutron has 3 quarks. Let there be n ‘up quark’ in a neutron and (3-n) ‘down quark’

Charge due to n ‘up quark’ = + $(\frac{2}{3}$ e)n

Charge due to (3-n) ‘down quark’ =  $<br>$- (

Since total charge of a neutron is zero, we get

+ $(\frac{2}{3}$e)n -( $\frac{1}{3}e\left)\right(3-n)$ = 0

$\frac{\mathrm{<br>}}{}$ $(\frac{2}{3}$ e)n = ( $\frac{1}{3}e\left)\right(3-n)$

en = e or n = 1

Hence number of ‘up quark’ in neutron = 1

Number of ‘down quark’ in neutron = 3-1 = 2

Therefore a neutron can be represented as ‘udd’.

 

Q.1.32

(a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at a null point (i.e., where E = 0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.

(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.

Ans.1.32 Let the equilibrium of the test charge be stable. If a test charge is in equilibrium and displaced from its position in any direction, then it experiences a restoring force towards a null point, where the electric field is zero. All the field lines near the null point are directed inwards towards the null point. There is a net inward flux of electric field through a closed surface around the null point. According to Gauss’s law, the flux of electric field through a surface, which is not enclosing any charge, is zero. Hence, the equilibrium of the test charge can be stable.

Two charges of same magnitude and same sign are placed at a certain distance. The mid-point of the joining line of the charges is the null-point. When a test charge is displaced along the line, it experiences a restoring force, If it is displaced normal to the joining line, then the net force takes it away from the null point. Hence, the charge is unstable because stability of equilibrium requires restoring force in all directions.

 

Q.1.33 A particle of mass m and charge (–q) enters the region between the two charged plates initially moving along x-axis with speed ${\mathit{v}}_{\mathit{x}}$ (like particle 1 in Fig. 1.33). The length of plate is L and a uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is $\frac{\mathit{q}\mathit{E}{\mathit{L}}^2}{2\mathit{m}{\mathit{v}}_{\mathit{x}}^{}}$

Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.

Ans.1.33 Charge on a particle of mass m = -q

Velocity of the particle = $v_x$

Length of the plates = L

Magnitude of the uniform electric field between the plates = E

Mechanical force, F = Mass (m) $\times$ Acceleration (a)

a = $\frac{F}{m}$

a = $\frac{qE}{m}$ ………(1) { as electric force F = qE }

Time taken by the particle to cross the field of length L is given by.

t  =  $\frac{Lengthoftheplate}{Velocityoftheparticle}$ = $\frac{L}{v_x}$…………..(2)

In the vertical direction, initial velocity, u = 0

From the relation s = ut + $\frac{1}{2}$a $t^2$

We get, s = 0 + $\frac{1}{2}\frac{qE}{m}({\frac{L}{v_x})}^2$

s = $\frac{qe{L}^2}{2m{v_x}^2}$

Hence, vertical deflection of the particle at the far edge of the plate is $\frac{qe{L}^2}{2m{v_x}^2}$ . This is similar to the motion of horizontal projectiles under gravity.

Q.1.34 Suppose that the particle in Exercise in 1.33 is an electron projected with velocity  = 2.0 × 10⁶ m s^–1. If E between the plates separated by 0.5 cm is 9.1 × 10² N/C, where will the electron strike the upper plate? (|e|=1.6 × 10^–19 C, m_e = 9.1 × 10^–31 kg.)

Ans.1.34 Velocity of the particle, $v_x$ = 2.0 $\times {10}^6$m/s

Separation of the two plates, d = 0.5 cm = 0.005 m

Electric field between two plates, E = 9.1 $\times {10}^2$ N/C

Charge of an electron, q = 1.6 $\times {10}^{-19}$ C

Mass of an electron, $m_e$ = 9.1 $\times {10}^{-31}$ kg

Let the electron strike the upper plate at the end of the plate L, when deflection is s. Therefore

s = $\frac{qe{L}^2}{2m{v_x}^2}$

L =  $\sqrt[]{\frac{2sm{v_x}^2}{qE}}$ =  $\sqrt[]{\frac{2\times 0.005\times 9.1\mathrm{}\times {10}^{-31}\times ({2.0\mathrm{}\times {10}^6)}^2}{1.6\mathrm{}\times {10}^{-19}\times 9.1\mathrm{}\times {10}^2}}$ = $\frac{\mathrm{<math>\; <mo>\; 3.64\times \; </mo>\; <msup>\; <mrow>\; <mrow>\; <mn>\; 10\; </mn>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mo>\; -\; </mo>\; <mn>\; 20\; </mn>\; </mrow>\; </mrow>\; </msup>\; </math>}}{1.456{{\mathrm{<math>\; <mo>\; \times \; </mo>\; <msup>\; <mrow>\; <mrow>\; <mn>\; 10\; </mn>\; </mrow>\; </mrow>\; <mrow>\; <mrow>\; <mn>\; -16\; </mn>\; </mrow>\; </mrow>\; </msup>\; </math>}}_{\mathrm{<br>}}}^{\mathrm{<br>}}}$= 0.0158 m = 1.58 cm

Therefore, the electron will strike the upper plate after travelling 1.58 cm.