Continuity and Differentiability: Overview, Questions, Preparation

The terms continuity and differentiability are crucial linking concepts that explain the linkage derivatives and limits. Continuity explains whether the function is continuous in a given interval. In contrast, differentiability is achievable when the slope of a function is possible to plot on a graph.

Concept of Continuity

Continuity of a function can be explained as the characteristics of a functional value and function. Moreover, it is a continuous function if the curve does not have any breaking or missing point on a given domain or interval. In short, the curve is continuous at each point of its domain.

It can be explained as:
limq→bf(q) exists, and
limq→bf(q) = f(b)

However, if the function does not exist or is undefined, it is a discontinuous function.

Continuity for the Closed Interval [x,y]

A function f(x) will be continuous for the closed interval [x,y] subjected to the satisfaction of the following conditions:

1. f(q) will be continuous for the open interval (x,y)
2. f(q) will be continuous at the point of right side, i.e., limq→x f(q)=f(x)
3. f(q) will be continuous at the point from left side, i.e., limq→y f(q)=f(y)

Concept of Differentiability

F(x) will be explained as differentiable at the point q = x if the derivative f ‘(q) exists at every single point of its domain. It can be demonstrated as:

F’(q) = Lim_h→0 f(x+h)-f(x)/h

Although a function differentiable at any point q = x within the domain must be continuous at that specific point, the vice-versa of that is not always true. 

Following are the derivatives of some basic trigonometric functions:

1. d/dA(sinA) = cosA
2. d/da (cosA) = sinA
3. d/dA (cotA) = -cosec²A
4. d/dA(cosecA) = -cosecA cotA
5. d/dA (tanA) = sec²A
6. d/dA (secA) = secA tanA

Continuity and differentiability are considered to be two strong pillars of Class 12th Calculus. Here students will learn the concepts of derivatives of a function, continuity at a point, continuity on an interval, and application of limiting properties on various complex and real numbers. The questions related to this topic are asked for 8-10 marks in boards.

1.

Solution:
Since f(x) is continuous at x=0
∴ lim x→0−​f(x)=f(0)=x→0+lim​f(x)
⇒lim x→0− ​(1+∣sinx∣) a/∣sinx∣​=b= lim x→0+  ​e tan²x/ tan³x​
⇒ea=b=e^2/3
∴a=2/3
And, ​a = loge​b

2. Interpret the continuity of the function f(A). If, f(A) = SinA . CosA
Solution:
Both Sin A and Cos A are continuous functions. However, the product of two continuous functions will also result in a continuous function.

Therefore, we can interpret that function f(A) = Sin A . Cos A is a continuous function.

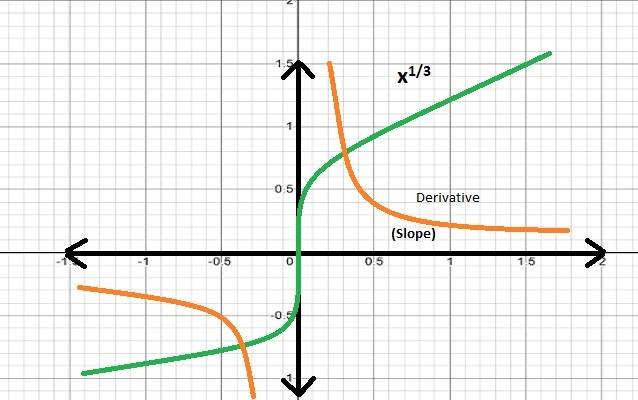
3. Analyse the differentiability of f (x) = x^1/3 for x = 0. 
Solution:
From the below figure, we can clearly observe that there is no break in the graph, so the given function is a continuous function.

Now, let us examine whether f’(0) exists or not. 

Now, f’(0) = Lim_x→0 f(x) – f(0)/ x- 0 = Lim_x→0 x^1/3- 0/ x
= Lim_x→0 x^-2/3    
= Lim_x→0 1/ x^2/3 → ∞

Q: Is it vice versa if differentiability into continuous function exists?

Q: Can differentiability be measured for open and close intervals?

Q: How will you know that a function is differentiable on the open interval?

Q: What does "no break in the curve" represent?

Q: What is a discontinuous function?