Rachit Kumar SaxenaManager-Editorial
What is Mensuration?
Mensuration is the measurement of geometric figures. This chapter will learn about some additional quadrilaterals, their areas, perimeter, surface areas, and volumes.
Trapezium:
A trapezium is outlined by a form that has 2 parallel sides, and the other 2 are nonparallel. It has four sides and four vertices.
| Shape |
Area |
Perimeter |
|---|---|---|
| 1. Trapezium |
Area= (1/2) H + (AB+CD) |
P= sum of all the sides i.e. AB+BC+CD+AD |
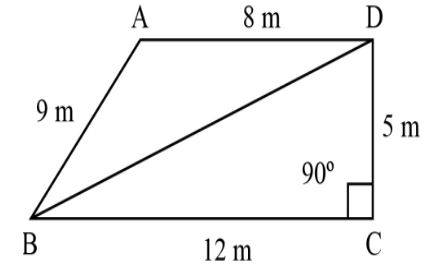
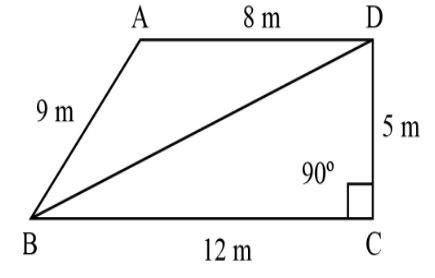
| 2. General quadrilateral |
Area= Area of △ABC + Area of △ADC |
The perimeter depends on the type of shape which is present |
| 3. Special quadrilateral (rhombus) |
½ × d1 × d2 |
P=4a |
Where, H= height, W= breadth, a,b,c,d= sides, d= diagonals
Quadrilateral
Surface area: The definition is that the total area of all the surfaces of any form.
Volume: the degree is outlined by the number any third-dimensional form takes.
Solid shapes:
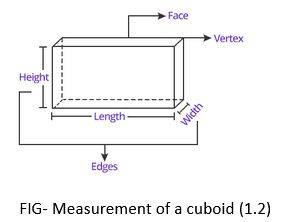
Solid shapes are measured by their three-dimensional structure with outlined breadth, height and length. A cube, sphere, cylinder, cuboid are solid shape examples.
| Shape |
Surface area |
Volume |
|---|---|---|
| 1. Cube |
Area= 6a^2 |
V= a^3 |
| 2. Cuboid |
Area= 2 [(l × b) + (l× h) + (b× h)] |
V= l*w*h |
| 3. Cylinder |
Ares= 2πr (r + h) |
V= πr2 × h |
Where, H= height, a= sides, r= radius, d= diameter, b= breadth, w= width
Weightage and Importance of Mensuration
The chapter Mensuration is in class 8. It is chapter 11 of NCERT textbook. The weightage is 15% of the total marks.
Illustrated example on Mensuration
1. Calculate the area of a rhombus whose diagonals 10 cm and 8.2 cm of length.
Solution:
The formula for calculating area of a rhombus = ½ d1d2, (d1 and d2 are the lengths of the diagonal)
a= 2 × 10 × 8.2 cm2 = 41 cm2.
2. A rhombus with an area of 240cm2 and whose one diagonal is of length 16 cm. Find the other diagonal.
Solution:
We know d1 = 16 cm and let the other diagonal = d2
Thus the area of the rhombus = 2 d1 . d2 = 240,
So, ½ 16 d2 = 240
Therefore, d2= 30cm.
Diagonal 2 is 30 cm.
3. A cuboid-shaped aquarium is a present whose external measurements are of 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Solution: The length of the aquarium = l = 80 cm
Width of the aquarium (b) = 30 cm
Height of the aquarium (h) = 40 cm
Thus the area of the base = 80 × 30 = 2400 cm2 ,
Area of the side face = 30 × 40 = 1200 cm2 &
Area of the back face = 80 × 40 = 3200 cm2
Thus area required to be calculated = Area of the base + area of the back face + (2 × area of a side face)
= 2400 + 3200 + (2 × 1200) = 8000 cm2
FAQs on Mensuration
Q: What is the formula of the area of a cube?
Area=6a^2
Where a= sides of the cube
Q: What is the area of the quadrilateral?
Example: area of general quadrilateral= space of △ABC + Area of △ADC
Q: What is the height of a cylindrical structure?
Q: How many edges and faces will a cuboid have?
Q: What is the area of a cuboid?
Where, l= length, h=height, b= breadth
News & Updates
Mensuration Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test