
Class 12 Chapter 6 Application of Derivatives NCERT Solutions: Shiksha has provided complete NCERT solutions for Class 12 Chapter 6 Application of Derivatives to help students. This chapter is commonly known as Class 12 AOD amongst the students. In an earlier chapter of the Class 12 Calculus unit, students learned about finding derivatives of composite functions, inverse trigonometric functions, implicit functions, exponential functions and logarithmic functions. Class 12 Math Chapter 6 Application of Derivatives focuses on the application of all the derivatives concepts and formulae learned in the previous chapter in real-life problems.
Class 12 Math Chapter 6 Application of Derivative is a very fruitful chapter for both board and entrance exam students and its concepts are used in Physics and other Math chapters also. Shiksha has prepared a complete Application of Derivatives NCERT Solutions of NCERT Textbook by our experts. Students can also access the complete Exercise-wise NCERT Class 12 chapter 6 Application of Derivatives solution PDF on this page.
Students can use the Application of Derivatives Class 12 Math Solution PDF to strengthen their concepts for CBSE Boards as well as other Entrance exams such as JEE Main, KCET, etc. Students should also check the Class 12 Chapter 5 Continuity and Differentiability NCERT solutions to get a better understanding of the Application of Derivatives.
Application of Derivatives explores many key topics such as the rate of change of quantities, increasing and decreasing functions, tangents & normals, approximations, and Minima & Maxima. Students can access the complete Class 11 Math chapter-wise Solutions and Class 12 Chapter-wise Math solutions on Shiksha. For more information check below;
| Related Important Math Chapter Solutions | ||
|---|---|---|
| Class 12 Chapter 9 Differential Equations | Class 12 Chapter 7 Integrals | Class 12 Chapter 8 Application of Integrals |
- Class 12 Math Chapter 6 Application of Derivatives: Key Topics, Weightage & Important Formulae
- Class 12 Math Chapter 6 Application of Derivatives Solution PDF: Free Download
- Class 12 Application of Derivatives Exercise 6.1 Solutions
- Class 12 Application of Derivatives Exercise 6.2 Solutions
- Class 12 Application of Derivatives Exercise 6.3 Solutions- (Old NCERT)
- Class 12 Application of Derivatives 6.4 Solutions- (Old NCERT)
- Class 12 Application of Derivatives 6.5 Solutions- (Old NCERT)
- Class 12 Application of Derivatives Miscellaneous Exercise Solutions
- Class 12 Math important reference books and preparation Tips
Class 12 Math Chapter 6 Application of Derivatives: Key Topics, Weightage & Important Formulae
Class 12 Math Chapter 6 Application of Derivatives has significant weight in board examinations, contributing between 8–10 marks. Application of Derivatives also has a significant weight in competitive exams directly 1-2 questions are asked from related concepts in JEE Main, and indirectly since it is useful in calculus, 3D and 2D geometry, and Physics chapters. Students can check the key topics and formulae of Application of derivatives chapters below;
Class 12 Application of Derivatives Key Topic
- Rate of Change of Quantities
- Increasing and Decreasing Functions & Determining intervals where a function is increasing or decreasing using differentiation.
- Finding Tangents and Normals using the first-order derivative concept.
- Applications of Derivatives in Two-dimensional geometry and conic section of classes 11 and 12.
- Finding Maxima and Minima using first and second-order derivatives
Check out the Chapter 6 Application of Derivatives Dropped Topics – 6.4 Tangents and Normals, 6.5 Approximations, Examples 45, 46, Ques. 1, 4–5 and 20–24 (Miscellaneous Exercise), Page 245 Points 4–10 in the Summary
Application of Derivatives Important Formulae for CBSE and Competitive Exams
- Rate of Change: , where is the dependent variable and is the independent variable.
- Slope of Tangent:
- Slope of Normal:
- Equation of the tangent:
- Equation of the normal:
- Approximation Formula:
- Condition for Increasing Function:
- Condition for Decreasing Function:
- Local Maxima/Minima (First Derivative Test): Solve and analyze sign changes of around the critical points.
- Conditions for Minima and Maxima:
-
- and for local minima.
- and for local maxima.
-
- Second Derivative Test: Use to confirm the nature of critical points.
Class 12 Math Chapter 6 Application of Derivatives Solution PDF: Free Download
Students can find the complete exercise-wise solution of the Class 12 Application of Derivatives NCERT PDF in one place designed by our experts. This Class 12 Application of Derivatives Solution PDF for NCERT Textbook is helpful for all students in various aspects. Both CBSE boards and competitive exams aspirants; JEE Main, CUSAT CAT, BITSAT, etc... Students can access the Application of Derivatives Class 12 solutions pdf download for free below;
Class 12 Math Chapter 6 Application of Derivatives Solution PDF: Free PDF Download
Class 12 Application of Derivatives Exercise 6.1 Solutions
Class 12 Application of Derivatives Exercise 6.1 discusses the fundamental usage of Derivative techniques to solve various kinds of problems. Application of Derivatives Exercise 6.1 focuses on the rate of change of quantities, increasing and decreasing functions, tangents and normals, approximations, and finding maxima and minima. The concepts discussed in Class 12 Math Exercise 6.1 Solutions will help students get a good understanding of calculus and even provide tools to solve problems in Class 12 physics and other fields too. Class 12 Ch 6 Exercise 6.1 Solutions includes 18 Questions (10 Long, 6 Short, 2 MCQs). Students can check the complete solutions for Exercise 6.1 below;
Application of Derivatives Exercise 6.1 Solutions
Q1. Find the rate of change of the area of a circle with respect to its radius r when
(πr2) = 2πr.
A.1. (a) r = 3cm
When r = 3 cm,
= 2 × π × 3 cm = 6π.
Thus, the area of the circle is changing at the rate of 6π cm .
(b) r = 4cm
whenr = 4cm,
= 2 × π × 4cm = 8π.
Thus, the area of the circle is changing at the rate of 8 .
Q2. The volume of a cube is increasing at the rate of 8 cm3 /s. How fast is the surface area increasing when the length of an edge is 12 cm?
A.2. Let x be the length of edge,v be the value and s be the surface area of the cube then,
y = x3.
and S = 6x2, where x is a fxn of time.
Now,
(x3) = 8
(by chain rule)
3x2
Now, (bx2) = = 12x .
When x = 12 cm,
.
Q3. The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A.3. Let ‘r’ cm be the radius of the circle which is afxn of time.
Then, = 8 3cm/s as it is increasing.
Now, the area A of the circle is A = πr2.
So, the rate at which the area of the circle change πr2.
= 2πr 3
= 6πr.
When r = 10cm,
= 6.π × 10 = 60π
Q4. An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
A.4. Let ‘x’ cm be the length of edge of the cube which is a fxn of time t then,
= 3cm/s as it is increasing.
Now, volume v of the cube is v = x3
Ø Rate of change of volume of the cube
= 3x2.3
= 9x2
When x = 10cm.
= 9 x (10)2= 900
Q5. A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
A.5. The area A of the circle with radius π is A = πr2
Then, rate of change in area =
= 2πr
Q The wave moves at a rate 5cm/s we have,
= 5cm/s
So, =r. 5 = 10πr.
When r = 8 cm.
= 10.π.8 cm = 80 × cm
Q6. The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
A.6. The circumference C of the circle with radius r is C = 2πr.
Then, rate of change in circumference is =
Q Radius of circle increases at rate 0.7 cm/s we get,
cm/s
So, = 2.× 0.7 cm/s = 1.4 × cm/s.
Q7. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
A.7. Since the length x is decreasing and the widthy is increasing with respect to time we have
= 5cm/min and = A cm/min
(a) The perimeter P of a rectangle will be, P = 2(x + y)
Q Rate of change of perimeter,
= 2( -5 + 4)
= -2 cm/min
(b) The area A of the rectangle is A = x. y.
Rate of change of area is
= 4x - 5y
So, |x = 8ay = 6cm = 4(8) - 5(6) = 32 - 30 = 2 cm2/min spherical balloon
Q8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm
A.8. Let ‘r’ cm be the radius of volume V. measured Then,
Now, rate at which balloon is being inflated = 900
= 900
× 3 × r2 = 900.
When r = 15cm,
= cm/s.
Q Radius of balloon increases by per second.
Q9. A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm
A.9. The volume v of a spherical balloon with radius r is V.
with respect its radius.
Then, the rate of change of volume
= 4 r2
Whenx = 10 cm,
= 4 10)2 = 400 cm3/cm
Q10. A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?
A.10. Since, the bottom of ground is increasing with time t,
= 2cm/s
From fig, Δ ABC, by Pythagorastheorem
AB2 + BC2 = AC2
x2 + y2 = 52
x2 + y2 = 25 ____ (1)
Differentiating eqn (1) w. r. t. time t we get,
m/s
When x = 4m, the rate at which its height on the wall decreases is
room
Q11. A particle moves along the curve 6y = x3 +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate
A.11. Given eqn of the curve is 6y = x3 + 2.______ (1)
Wheny coordinate change s 8 times as fast as x-coordinate
= 8 _____ (2)
Now, differentiating eqn (1) wrt.x we get,
6 × 8 = 3x2 (using eqn(2))
x = 4.
When x = 4, we have, 6y = 43+ 2 = 64 + 2 + 66
y =11.
And when x = -4, we have, 6y = ( -4)3 + 2 = -64 + 2 = -62
The tequired point s are (4, 11) and
Q12. The radius of an air bubble is increasing at the rate of 1 2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A.12. Let x be the radius of the bubble with volume .V. then,
cm/s
andV =
Rate of change of volume =
= 4πr2 ×
= 2πr2.
= 2x(1)2 2π.
Q13. A balloon, which always remains spherical, has a variable diameter 3 (2 1) 2 x + . Find the rate of change of its volume with respect to x.
A.13. Given, diameter of the spherical balloon = (2x + 1)
So, radius of the spherical r =
Then, volume of the spherical V =
Q Rate of change of volume wrt.tox,
Q14. Sand is pouring from a pipe at the rate of 12 cm3 /s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
A.14. Let r cm and h cm be the radius and the height of the cone. Then,
h = r. H = 6h
So, volume, V of the cone = πr2h
= 12 × h3
Rate of change of volume of the cone wrt the height is
= 12 × π × 3 × h2.
As the sand is pouring from the pipe at rate of 12
we have
Hence, the height is increasing at the rate of cm/s.
Q15. The total cost C (x) in Rupees associated with the production of x units of an item is given by C (x) = 0.007x3 – 0.003x2 + 15x + 4000.
Find the marginal cost when 17 units are produced.
A.15. Given, c(x) = 0.007 x3- 0.003x2 + 15x + 400.
Since the marginal cost is the rate of change of total cost wrt the output we have,
Marginal cost, MC, =
= 0.007 × 3x2- 0.003 × 2x + 15.
When x = 17,
Then, MC = 0.007 × 2. (17)2 - 0.003 2(17) + 15.
= 6.069 - 0.102 + 15.
= 20.967
Hence, the required marginal cost = ` 20, 97.
Q16. The total revenue in Rupees received from the sale of x units of a product is given by R (x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
A.16. Given, R(x) = 13x2 + 26x + 15.
Marginal revenue is the rate of change of total revenue with respect to the number of units sold Marginal revenue (MR) =
= 13 × 2x + 26
= 26x + 26
When x = 7,
MR = 26 × 7 + 26 = 182 + 26 = 208.
Hence, the required marginal reverse = ` 208.
Choose the correct answer for questions 17 and 18.
Q17. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π (B) 12π (C) 8π (D) 11π
A.17. The area A of the isle with radius r is given by with respect to radius r A = πr2.
Then, rate of change of area of the circle
= 2πr.
When r = 6 cm
Q option (B) is correct.
Q18. The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is
(A) 116 (B) 96 (C) 90 (D) 126
A.18. Given, R(x) = 3x2 + 36x + 5.
Marginal revenue,
= 3 × 2x + 36
= 6x + 36
When x = 15.
= 90 + 36 = 126
Option (D) is correct.
Class 12 Application of Derivatives Exercise 6.2 Solutions
Class 12 Application of Derivatives Exercise 6.2 Solutions will be a comprehensive guide for students covering all concepts, formulae, and more. Class 12 Math NCERT Exercise 6.2 focuses on advanced applications of derivatives, including determining the monotonicity of functions, identifying points of local maxima and minima, and solving related problems. These topics will be very helpful for the students preparing for competitive exams such as JEE, BITSAT, and more. Application of Derivatives Exercise 6.2 Solutions will include explanations of 19 Questions (10 Long, 7 Short, 2 MCQs). Students can check the complete solution of Exercise 6.2 below;
Application of Derivative Exercise 6.2 Solutions
Q1. Show that the function given by f (x) = 3x + 17 is increasing on R.
A.1. We have,.
f (x) = 3x + 17.
So, f (x) = 3 > 0
∴f (x) is strictly increasing on R.
Q2. Show that the function given by f (x) = e2x is increasing on R.
A.2. We have, f (x) = e2x
So, f (x) = = = 2e2x> 0
∴f (x) is strictly increasing on R.
Q3. Show that the function given by f (x) = sin x is (a)
increasing in (b) decreasing in
(c) neither increasing nor decreasing in
A.3. We have, f (x) = sin x.
So, f (x) = cosx.
(a) when,x ∈ i e, x in 1st quadrat.
f(x) = cos.x> 0
f (x) is strictly increasing in .
(b) when,x ∈ in IInd quadrat
f(x) = cosx< 0.
∴f(x) is strictly decreasing(π
(c) When ,x ∈(0,π).
f(x) = cosx is increasing in and decreasing
in and f = cos
∴f (x) is neither increasing not decreasing in (0,π).
Q4. Find the intervals in which the function f given by f(x) = 2x2 – 3x is
(a) increasing (b) decreasing
A.4. We have, f (x) = 2x2 3x
So, f(x) =
Atf (x) = 0.
4x - 3 = 0
i e, divides the real line into two
disjoint interval
(a) Now,
f(x) = 4x - 3 > 0
So, f (x) is strictly increasing in
(b) Now, f (x) = 4x - 3 < 0
So, f (x) is strictly decreasing in
Q5. Find the intervals in which the function f given by f(x) = 2x3 – 3x2 – 36x + 7 is
(a) increasing (b) decreasing
A.5. We have, f (x) = 2x3- 3x2- 36x + 7.
So, f (x) =
= 6 (x2-x- 6).
= 6 (x2- 3x + 2x- 6)
= 6 [x (x- 3) + 2 (x- 3)]
= 6 (x- 3) (x + 2).
At, f (x) = 0
6 (x- 3) (x + 2) = 0.
So, when x- 3 = 0 or x + 2 = 0.
x = 3 or x = -2.
Hence we an divide the real line into three disjoint internal
I
At x ∈
f(x) = ( + ve) ( -ve) ( -ve) = ( + ve) > 0.
So, f (x) is strictly increasing in
At, x∈( -2,3),
f(x) = ( + ve) ( + ve) ( -ve) = ( -ve) < 0.
So, f (x) is strictly decreasing in ( -2,3).
At, x ∈
f (x) = ( + ve) ( + ve) ( + ve) = ( + )ve> 0.
So, f (x) is strictly increasing in
∴ (a) f (x) is strictly increasing in
(b) f (x) is strictly decreasing in ( -2,3)
Q.6. Find the intervals in which the following functions are strictly increasing or decreasing:
(a) x2 + 2x – 5 (b) 10 – 6x – 2x2 (c) –2x3 – 9x2 – 12x + 1 (d) 6 – 9x – x2
(e) (x + 1)3 (x – 3)3
A.6. (a) f (x) = x2 + 2x - 5.
f(x) = 2x + 2 = 2 (x + 1).
At, f(x) = 0
2 (x + 1) = 0
x = -1.
At, x
f(x) = (- ) ve< 0.
So, f (x)is strictly decreasing or
At x ∈
f(x) = ( + ve) > 1
f(x) is strictly increasing on
(b) f(x) = 10 - 6x- 2x2
So, f(x) = - 6 - 4x = - 2 (3 + 2x).
Atf(x) = 0
2 (3 + 2x) = 0.
x =
At x
∴f(x) is strictly increasing on
At x
f(x) = ( -ve) ( + ve) = ( - ) ve< 0.
∴f (x) is strictly decreasing on
(c) f (x) = 2x3- 9x2- 12x.
So, f (x) =- 6x2- 18x- 12 = - 6 (x2 + 3x + 2).
= -6 [x2 + x + 2x + 2]
= -6 [x (x + 1) + 2 (x + 1)]
= -6 (x + 1) (x + 2)
At, f (x) = 0.
6 (x + 1) (x + 2) = 0
x = -1 and x = -2.
At, x , f(x) = ( -ve) ( -ve) ( -ve) = ( -ve) < 0
So, f(x) is strictly decreasing.
At, x( -2, -1), f(x) = ( -ve) ( -ve) ( -ve) = ( -ve) < 0.
So, f(x) is strictly decreasing
(d)f(x) = 6 - 9x-x2
So, f(x) = - 9 - 2x
At, f(x) = 0
9 - 2x = 0
x =
At, x ∈
f(x) > 0
So, f(x) is strictly increasing.
At x ∈
f(x) < 0.
So, f(x) is strictly decreasing.
(e) f(x) = (x + 1)3 (x- 3)3.
So, f(x) = (x + 1)3
= (x + 1)3. 3 (x- 3)2 + (x- 3)3. 3 (x + 1)2
= 3 (x + 1)2 (x- 3)2 (x + 1 + x- 3).
= 3 (x + 1)2 (x- 3)2 (2x- 2).
= 6 (x + 1)2 (x- 3)2 (x- 1).
For strictly increasing,
f(x) > 0.
As 6 > 0,(x + 1)2> 0 and (x- 3)2> 0. We need
(x 1) > 0.
x> 1.
∴f (x) is strictly increasing on
And strictly decreasing on
Q7. Show that 2 log(1 ) 2 x y x x = +− + , x > – 1, is an increasing function of x throughout its domain.
A.7. We have, y = log
Differentiating the above wrt.x.we get,
The given domain of the given function isx> -1.
(x + 1) > 0.
Also,
(2 + x)2> 0.
Hence,
∴ y is an increasing function of x throughout its domain.
Q8. Find the values of x for which y = [x(x – 2)]2 is an increasing function.
A.8. We have, y = [x (x- 2)]2.
Differentiating the above w rt. x we get,
= 2 [x (x- 2)] (x + x- 2)
= 2x (x - 2) (2x - 2)
= 4x (x - 2) (x - 1).
Now,
4x (x - 2) (x - 1) = 0.
i e, x = 0, x = 2, x = 1 divides the real line into
four disjoint interval. [0,1],[1,2] and
when x
∴f (x) is decreasing in
When
∴f (x) is increasing in [0,1].
When x
∴f (x) is decreasing.
When
∴f (x) is in creasing
Hence, f (x) is increasing for x
Q9. Prove that is an increasing function of θ .
A.9. We have, y =
Differentiating w rt.Ø we get,
When we know that,
So,
And also, (2 + cos )2> 0.
Hence, y is an increasing fxn of in
Q10. Prove that the logarithmic function is increasing on (0, ∞).
A.10. We have, f (x) = log x.
So, f (x) =
i e, f (x) > 0. When
Hence, the logarithmic fx is strictly increasing on
Q11. Prove that the function f given by f(x) = x2 – x + 1 is neither strictly increasing nor decreasing on (– 1, 1).
A.11. We have, f(x) = x2-x + 1.
So, f(x) =
Atf(x) = 0.
2x - 1 = 0
I e, x = divides the real line into two disjoint interval the interval ( -1, 1) into
Two disjoint interval
And f(x) is strictly increasing in and strictly decreasing in
Hence, f(x) is with a increasing or decreasing on ( -1,1).
Q12. Which of the following functions are decreasing on ?
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
A.12. (A) We have,
f(x) = cosx
So, f(x) = -sin x
When x we know that sin x> 0.
-sinx< 0. f(x) < 0
∴f(x) is strictly decreasing on
(B) We have, f(x) = cos 2x
So, f(x) = -2sin 2x
When we know that sin x> 0.
i e, 0
So, sin 2x> 0 (sinØ is ( +ve) in 1st and 2ndquadrant).
-2sin 2x< 0.
f (x) < 0.
∴f (x) is strictly decreasing on
(c) We have, f(x) = cos 3x
f(x) = -3 sin 3x.
As
We can divide the interval into two
Case I At, 0 < 3x
sin 3x> 0.
-3 sin 3x< 0
f(x) < 0.
∴f(x) is strictly decreasing on
case II. At
sin 3x< 0.
-3 sin 3x> 0.
f(x) > 0.
∴f(x) is strictly increasing on
Hence, f(x) is with a increasing or decreasing on
(d)we have, f(x) = tan x.
So, f(x) = sec2x.
f(x) = sec2x> 0
∴f(x) is strictly increasing on
Hence, the fxncosx and cos 2x are strictly decreasing on
Q13. On which of the following intervals is the function f given by f(x) = x100 + sin x –1 decreasing ?
(A) (0,1) (B) , (C) (D) None of these
A.13. We have, f (x) = x 100 + sin x - 1.
So, f (x) = 100x99 + cosx.
(A) When x (0,1). We get.
x>0
x99> 0
100 x99> 0.
Now, 0 radian = 0 degree
and 1 radian =
So, cosx> 0 for x∈ (0,1) radian = (0,57)
∴f (x) > 0 for x∈ (0,1).
(B) When x ∈ we get,
So, x> 1
x99> 1
100x99> 100.
And cosx is negative between -1 and 0.
So, f (x) = 100x99 + cosx> 100 - 1 = 99 > 0.
∴f(x) is strictly increasing on
(c) When x ∈ we get,
x> 0
x99> 0
100x99> 0
andcosx> 0. (firstquadrant).
I e, f(x) > 0.
∴f(x) is strictly increasing on
Hence, option (D) is correct.
Q14. For what values of a the function f given by f(x) = x2 + ax + 1 is increasing on [1, 2]?
A.14. We have, f(x) = x2 + x + 1
So, f(x) = 2x + a
If f(x) is strictly increasing onx
So, 1
The minimum value of f (x) is 2 + a and that of men value is 4 + a.
∴ 2 +a> 0and 4 + a> 0
a> -2 and a> -4.
a> -2.
∴The best value of a is -2.
Q15. Let I be any interval disjoint from [–1, 1]. Prove that the function f given by
is increasing on I.
A.15. We have,f(x) =
So, f(x) =
So, for every x∈ I, where I is disjoint from [-1,1]
f(x) =
and f(x) = = ( + ve) > 0 when x< -1.
∴f(x) is strictly increasing on I .
Q16. Prove that the function f given by f(x) = log sin x is increasing on and decreasing on .
A.16. We have, f(x) = log sin x
So, f(x) =
When
f(x) = cot x> 0 (Ist quadrat )
So, f(x) is strictly increasing on
When x ∈
f(x) = cot x< 0. (IIndquadrant ).
So, f (x) is strictly decreasing on
Q17. Prove that the function f given by f (x) = log |cos x| is decreasing on and increasing on
A.17. We have, f (x) = log
f(x) =
whenx we get.
tanx> 0 (Ist quadrant).
tanx< 0
f(x) < 0.
∴f (x) is decreasing on
When x ∈ we get,
tanx|< |0 (ivth quadrant).
-tanx|>| 0
f(x) > 0
∴f(x) is increasing on
Q18. Prove that the function given by f (x) = x3 – 3x2 + 3x – 100 is increasing in R.
A.18. We have, f(x) = x3- 3x2 3x- 100.
So, f(x) = 3x2- 6x + 3 = 3 (x2- 2x + 1) = 3 (x- 1)2
For
(x- 10)2 , 0 for x = 1.
3 (x- 1)2
f(x)
∴f(x) is increasing on
Q19. The interval in which y = x2 e–x is increasing is (A) (– ∞, ∞) (B) (– 2, 0) (C) (2, ∞) (D) (0, 2)
A.19. We have, f(x) = x2 e–x
So, f(x) =
= -x2 e-x + e-x 2x.
= x e-x( x + 2).
If f (x) = 0.
x = 0, x = 2.
Hence, we get there disjoint interval
When, x we have, f (x) = ( -ve) ( + ve) = ( -ve) < 0.
So, f is strictly decreasing.
When x ∈(0,2), f (x) = ( + ve) ( + ve) = ( + ve) > 0.
So, f is strictly increasing.
And when x ∈ f (x) = ( +ve) ( -ve) = ( -ve) < 0.
So, f is strictly decreasing.
Hence, option (D) is correct.
Class 12 Application of Derivatives Exercise 6.3 Solutions- (Old NCERT)
Class 12 Application of Derivatives Exercise 6.3 focuses on several important concepts such as finding tangents and normals, their equations, and the geometric interpretation of slopes at specific points on a curve using the application of derivatives. Application of Derivatives Exercise 6.3 Solutions will have the explanation of 27 Questions including 14 Long, 11 Short, and 2 MCQs. Students can check the complete Class 12 Math Exercise 6.3 NCERT solutions below;
Application of Derivatives Exercise 6.3 Solution
Q1. Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
A.1. The given eqn of the curve is
Slope of the tangent at x = 4 is given by
= 764
Q2. Find the slope of the tangent to the curve
A.2. The given eqn of the curve is
Slope of tangent at x = 10 is given by,
Q3. Find the slope of the tangent to curve y = x3 – x + 1 at the point whose x- coordinate is 2.
A.3. Slope of tangent to the given curve is
So,
Q4. Find the slope of the tangent to the curve y = x3 –3x + 2 at the point whose x-coordinate is 3.
A.4. Slope of tangent to the given curve is
so,
Q5. Find the slope of the normal to the curve
A.5. The Equation of the given curve are
So,
and
So, which is the slope of the tanget to the curve.
Now, required slope of normal to the curve =
Q6. Find the slope of the normal to the curve
A.6. The given eqn of the curves are
so,
Slope of tangent to curve at is
Hence, slope of normal to curve
Q7. Find points at which the tangent to the curve y = x3 – 3x2 – 9x + 7 is parallel to the x-axis.
A.7. The given eqn of the curve is
slope of tangent to the given curve,
when the tangent is parallel to x-axis
x = 3 or x = -1
When x = 3,
And when x = -1
Hence, the required points are
Q8. Find a point on the curve y = (x – 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4)
A.8. Let the point joining the chord be
Then slope of the chord
= 2
The given eqn of the curve
slope of the tangent to the curve
Given that, the tangent is parallel to the chord PQ.
slope of tangent = slope of PQ.
and
The required point on curve is
Q9. Find the point on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11.
A.9. The given eqn of the curve is
slope of tangent to the curve
Then eqn of tangent is which gives us slope
So,
When x = 2,
And when x = 2,
The point when put into we get
which is true.
and the point when put into gives,
which is not true.
Hence, the required point is .
Q10. Find the equation of all lines having slope – 1 that are tangents to the curve
A10. The given eqn of curve is
Slope of tangent to the given curve is
Given that, slope of tangent = 1.
ie, X=1+1 or
or
When
and when
Hence, the point of contact of the tangents are
The reqd. eqn of line are
and
and
and
Q11. Find the equation of all lines having slope 2 which are tangents to the curve
A.11. The given eqn of curve is
Slope of tangent to the curve is
Given,
which is not possible
we conclude that there is no possible tangent to the given curve with slope = 2.
Q12. Find the equations of all lines having slope 0 which are tangent to the curve
A.12. The given eqn of the curve is
Slope of tangent to the curve is
Given,
When
The point of contact of the tangent to the curve is
The eqn of the line is
Q13. Find points on the curve at which the tangents are
(i) parallel to x-axis (ii) parallel to y-axis.
A.13. Diffrentiating wrt. X we get,
(i) When the tangent is || to x-axis, the slope of tangent is 0
ie,
putting this in the eqn of curve. We get,
The point at which the tangents are parallel to x-axis are
(ii) when the tangent is parallel to y-axis, the slope of the normal is 0.
ie,
, putting this in the eqn of curve we get,
The point at which the tangents are parallel to y-axis are
Q14. Find the equations of the tangent and normal to the given curves at the indicated points:
A.14. (i) we have,
slope of tangent,
slope of normal
Hence eqn of tangent at (0, 5) is
And eqn of normal at (0, 5) is
(ii) We have,
Slope of tangent,
= 30 28
= 2
Slope of normal
Hence eqn of tangent at (1, 3) is
And eqn of normal at (1,3) is
(iii) we have,
Slope of tangent,
And slope of normal
Hence, eqn of tangent at (1, 1) is
And eqn of normal at (1,1) is
(iv) We have,
Slope of tangent
So, eqn of the tangent at (0,0) is
ie, x- axis
Hence, the eqn of normal is x = 0 ie, y-axis
(v) We have,
So, slope of tangent
And slope of normal
Q15. Find the equation of the tangent line to the curve y = x2 – 2x +7 which is
(a) parallel to the line 2x – y + 9 = 0 (b) perpendicular to the line 5y – 15x = 13
A.15. The eqnof the given curve is
Slope of tangent,
(a) The line compared to gives,
Slope of line = 2.
If the tangent of the curve is parallel to the line
When
Hence, the point of contact of the tangent is (2, 7)
The eqn of tangent is
(b) The line
compared to gives
slope of line = 3
As the tangent to the curve is ⊥ to the line.
When we get
Hence, the point of contact of the tangent is
And eqn of the tangent is
Q16. Show that the tangents to the curve y = 7x3 + 11 at the points where x = 2 and x = – 2 are parallel.
A.16. The given eqn of the curve is .
Slope of tangent
and
The tangent to the given curve at x = 2 and x = -2 are parallel.
Q17. Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
A.17. The given eqn of the curve is .
Slope of tangent,
As, slope of tangent = y – coordinate of the point.
When
and when
The required points are
Q18. For the curve y = 4x3 – 2x5 , find all the points at which the tangent
passes through the origin.
A.18. The given eqn of the curve is
Slope of tangent, ________(1)
Let P(x, y) be the required point at the tangent passing through the origin (0,0)
Then, _________(2)
So, from (1) and (2) we get,
Putting this value of y in the eqn of curve we get,
or
or
When,
The required points are (0,0), (1,2) and (1,2)
Q19. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
A.19. The given eqnof the curve is ________(1)
Differentiating the given curve wrt.x we get,
slope of tangent
Given, tangent is || to x-axis
ie,
Putting x = 1 in eqn (1) we get,
Hence, the required points are (1,2) and (1, 2).
Q20. Find the equation of the normal at the point (am2 ,am3 ) for the curve ay2 = x3
A.20. The given eqn of curve is _____(1)
Differentiating eqn (1) wrt.x we get,
, slope of tangent
corresponding slope of normal
Hence, eqn of normal at is
Q21. Find the equation of the normals to the curve y = x3 + 2x + 6 which are
parallel to the line x + 14y + 4 = 0.
A.21. The given eqn of the curve is _____(1)
slope of tangent to the curve,
so, slope of normal to the curve
Now, the line compared to gives
slope of line =
As the normal is parallel to the line
When
and when
The point of contact of the normal are (2, 18) and (-2, -6)
Hence the eqn of normal are
and
Q22. Find the equations of the tangent and normal to the parabola y2 = 4ax at the point (at2 , 2at).
A.22. The given of the parabola is
slope of tangent is given by
so, slope of normal
so, slope of normal
Hence eqn of tangent at point is
And eqn of normal at point is
Q23. Prove that the curves x = y2 and xy = k cut at right angles* if 8k2 = 1.
A.23. The given eqn of the curves are
________(1)
and ___________(2)
Differentiating eqn (1) and (2) wrt ‘x’ we get,
_________(3)
and
_________(4)
Since the two curves cut each other at right angles we get,
________(5)
The point of intersection can be solve from eqn (1) and (2),
Hence, using eqn (5) we get,
Hence proved
Q24. Find the equations of the tangent and normal to the hyperbola
at the point
A.24. The given eqn of the hyperbola is ______(1)
Differentiating eqn (1) wrt ‘x’ we get,
is the reqd slope of tangent to the curve
So, eqn of tangent at point is
As lies on the parabola given by eqn (1) we write,
Hence,
Choose the correct answer in Exercises 26 and 27.
Q26. The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3 (B) (C) -3 (D) -
A.26. Given,
Slope of tangent,
So, slope of normal
Option (D) is correct.
Q27. The line y = x + 1 is a tangent to the curve y2 = 4x at the point (A) (1, 2) (B) (2, 1) (C) (1, – 2) (D) (– 1, 2)
A.27. The given eqn of curve is .
Then, differentiating wrt x we get,
which is the slope of the tangent to the curve.
The line compared to gives slope of line = 1.
Since, tangent is the line we have,
Putting y = 2 in we get,
Hence, the required point is
Option (A) is correct.
Class 12 Application of Derivatives 6.4 Solutions- (Old NCERT)
Class 12 Application and Derivatives
Q1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.
(i) √25.3
A.(i) Let y= √x : Let x = 25 and x = 0. 3.
Then, Δy = √x+Δx
= 5 + dy
=
= 5 + 0.03
(ii) √49.5
A.(ii)
Let y = √x Let x = 49 and x = 0.5.
Then,
= 7 + 0.0357.
(iii) √0.6
A.(iii)
Let y = √x Let x = 0.64 and Δx = 0.04.
Then,
= 0.8 - 0.025.
= 0.775.
(iv)
A.(iv)
Let Let x = 0.008 and Δx = 0.00 1.
Then, Δy =
= 0.2 + 0.0083.
= 0.208.
(v)
A.(v)
Let Let x = 1 and Δx = -0.001
Then,
= 0.999.
(vi)
A.(vi)
Let Then, x = 16 and Δx = 1.
Then,
(vii)
A.(vii)
Let Let x = 27 and Δx = 1.
Then,
(viii)
A.(viii)
Let Let x = 256 and Δx = 1.
Then,
(ix)
A.(ix)
Let let x = 81 and Δx = 1.
Then,
(x)
A.(x)
Let y = = √x Let x = 400 and Δx = 1.
Then,
(xi)
A.(xi)
Let Let x = 0.0036 and Δx = 0.0001
Then,
= 0.06 + 0.0008.
= 0.0608.
(xii)
A.(xii)
Let Let x = 27 and Δx = 0.43.
Then,
= 3 - 0.015.
= 2.985.
(xiii)
A.(xiii)
Let Let x = 81 and Δx = 0.5.
Then,
=
= 3 + 0.004 = 3.004.
(xiv)
A.(xiv)
Let Then x = 4 and Δx = 0.032.
Then,
=
= 8 - 0.096
= 7.904.
(xv)
A.(xv)
Let let x = 32 and Δx = 0.15.
Then,
= 2 + 0.0018
= 2.0018.
Q2. Find the approximate value of f(2.01), where f (x) = 4x2 + 5x + 2.
A.2. Given, y = f (x) = 4x2 + 5x + 2.
So, f (x) = 8x + 5. = 8x + 5 dy = (8x + 5) dx.
Let x = 2 and Δx = 0.01.Then,
f(x + Δx) = f(2 + 0.01) = f(2.01).
Δy = f.(x + Δx) f(Δx).
f(x +Δx) = f(x) +Δy.
= f(x) + dy = f(x) + (8x + 5) dx.
= f(2.01) = f(2) + (8 x 2 + 5). Δx{∴dx = Δx}
= 4 (2)2 + 5 (2) + 2 + 21 (0.01)
= 16 + 10 + 2 + 0.21 = 28.21.
Q3. Find the approximate value of f (5.001), where f(x) = x3 – 7x2 + 15.
A.3. Given, y = f(x) = x3- 7x2 + 15.
So,
dy = (3x2- 14x) dx.
Δy = (3x2- 14x) Δx.
Let, x = 5 and Δx = 0.001. Then,
Δy = f(x + Δx) f(x).
f(x + Δx) = f(x) + Δy = f(x) + (3x2- 4x) Δx.
f(5 + 0.001) = 53- 7(5)2 + 15 + [3(5)2 - 14(5)]. (0.001).
f(5.001) = 125 - 175 + 15 + (75 - 70) (0.001)
= -35 + 0.005 = - 34.995.
Q4. Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.
A.4. We know that, the volume v of side ‘a’ mete of cube is v = x3.
So,
Given that, increase in side = 1% of x.
Q5. Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%
A.5. We know that, the surface area 5 of a ‘x’ when length cube, is S = 6x2.
So,
Given decrease in side,
Q6. If the radius of a sphere is measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.
A.6. Let x be the radius of the sphere & Δπ be the error in measuring the radius.
Then, π = 7m and Δr = 0.02m.
Now, volume v of sphere is
So,
dv = 4π(7)2 (.0.02) = 3.92 πm3
∴The appropriate error is calculating the volume is 3.92πm3.
Q7. If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.
A.7. Let be the radius of the sphere &r be the error in measuring the radius.
Then, π = 9m and Δr = 0.03m.
Now, surface area S of the sphere is
S = 4πr2
So,
∴e, ds = Δr = 8πr.Δr = 8π × 9 × 0.03
= 2.16πm3.
Appropriate error in calculating the surface area is 2.16πm3.
Q8. If f(x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is (A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66
A.8. We have, y = f (x) = 3x2 + 15x + 5.
dy = (6x + 15) dx
Δy = (6x + 15) Δx.
Let, x = 3 and Δx = 0.02 then,
Δy = f(x + Δx) - f(x)
f(x + Δx) = f(x) + Δy = f(x) + (6x + 5) Δx.
f(3 + 0.02) = 3(3)2 + 15(3) + 5 + (6 × 3 + 15) (0.02).
f(3.02) = 27 + 45 + 5 + (18 + 15) (0.02).
= 77 + 0.66
= 77.66
∴ Option (D) is correct.
Q9. The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is (A) 0.06 x3 m3 (B) 0.6 x3 m3 (C) 0.09 x3 m3 (D) 0.9 x3 m3
A9. The volume v of a cube with side ‘x’ metre is v = x3
So,
∴increase in side, Δx = 3% of =
∴dv = 3x2π
Hence, option (C) is correct.
Class 12 Application of Derivatives 6.5 Solutions- (Old NCERT)
Class 12 Math Application of Derivatives Exercise 6.5 mainly focuses on problems such as finding minimum and maximum values of various types of functions, finding minima and maxima on a given point of functions, real real-world problems ( finding minimum and maximum profit), and finding values of volume, area, and more in a given interval for function. The Class 12 Exercise 6.5 Solutions will guide students about approaches, critical thinking skills, first and second derivative tests, and their applications in optimization. Application of Derivatives Exercise 6.5 consists of 29 Questions including 15 Long, 11 Short, and 3 MCQs. Students can check the complete solutions of the exercise 6.5 below;
Application of Derivative Exercise 6.5 Solutions
Q1.Find the maximum and minimum values, if any, of the following functions
given by.
(i)
A(i) We have, f(x) = (2x - 1)2 + 3.
For all
(2x - 1)2 + 3 ≥ 3.
f(x) ≥ 3.
∴The minimum value of f(x) = 3. When 2x - 1 = 0--> x =
Again as as there is vouppa bound to ‘x’ value hence, f(x) has no maximum values.
(ii)
A(ii)
We have, f(x) = 92 + 12x + 2.
(Taking 9 common from each team).
For all
f(x)≥ - 2.
∴The minimum value of f(x) = -2 when
And as so f(x) has
no maximum values.
(iii) f(x) = (x - 1)2 + 10
A(iii)
we have, f(x) = - (x - 1)2 + 10
For all
(x - 1)2 ≤ 0
-(x- 1)2 + 10 ≤ 10.
f(x) ≤ 10.
∴maximum value of f(x) = 10 when x - 1 = 0 x = 1.
And minimum value of f(x) does not exist.
(iv) g(x) = x3 + 1
A(iv)
we have, g(x) = x3 + 1
For the given fxn,
and
Q Maximum and minimum value does not exist.
Q2. Find the maximum and minimum values, if any, of the following functions
given by
(i) f(x) = |x + 2| - 1
A(i) we have, f(x) = |x + 2| - 1
We know that, for all
f(x) - 1.
∴ Minimum value of f(x) = -1 when x + 2 = 0 x = - 2.
And maximum value of f(x) does not exist.
(ii)
A(ii)
We have,
For all
g(x) 3.
∴ Maximum value of g(x) = 3 when
And minimum value does not exist.
(iii) h(x) = sin (2x) + 5.
A(iii)
we have, h(x) = sin (2x) + 5.
For all {range of sine function is [-1, 1]}
-1 + 5 sin 2x + 5 1 + 5.
4 h(x) 6.
∴ Maximum value of h(x) = 6.
Minimum value of h(x) = 4.
(iv)
A(iv)
we have,
As for all
-1 + 3 sin 4x + 3 1 + 3
2 f(x) 4.
∴ Maximum value of f(x) = 4.
Minimum value of f(x) = 2.
(v) h(x) = x + 1.,x∈ ( -1, 1).
A(v)
we have, h(x) = x + 1.,x∈ ( -1, 1).
Given, -1
- 1 + 1 <x + 1 < 1 + 1
0 <h (x) < 2.
∴ Maximum value and minimum value of h(x) does not exist.
Q3. Find the local maxima and local minima, if any, of the following functions.
Find also the local maximum and the local minimum values, as the case may be:
(i) f(x) = x2.
A(i) we have, f(x) = x2.
f(x) = 2x.
andf(x) = 2.
AR extreme point, f(x) = 0
2x = 0
x = 0.
When x = 0, f(0) = 2 > 0.
∴x = 0 is a point of local minima and value of local minimum is given by f(0) = 02 = 0.
(ii) g(x) = x3 3x
A(ii)
we have, g(x) = x3- 3x
g'(x) = 3x2- 3
g''(x) = 6x.
At extreme point,
g'(x) = 0
3x2- 3 = 0.
3(x2- 1) = 0 ⇒ 3(x - 1)(x + 1) = 0.
x = 1 or x = -1.
At x = 1, g"(1) = 6.1 = 6 > 0.
So, x = 1 is a point of local minima and value of local minimum is given by g(1) = 13- 3.1 = 1 - 3 = - 2.
And at x = -1, g"( -1) = 6 ( -1) = 6 < 0.
So, x = -1 is a point of local minima and value of local minimum is given by
g(- 1) = (- 1)3- 3(- 1) = 1 + 3 = 2.
(iii)
A(iii)
we have, h(x) = sin x + cos x.
h'(x) = cos x - sin x
h'(x) = -sin x - cos x.
At extreme points,
h'(x) = 0
cosx - sin x = 0
cosx = sin x
1 = tan x
(iv)
A(iv)
we have, f(x) = sin x cos x.
f(x) = cos x + sin x
f(x) = sin x + cos x.
At extreme points,
f(x) = 0
cosx + sin x = 0.
IInd quadrate or IIIth quadrate
A(v)
we have, f(x) = x3- 6x2 + 9x + 15.
At extreme point, f'(x) = 0.
At, x = 1,f"(1) = 6 × 1 - 12 = 6 - 12 = - 6 < 0
∴x = 1 is a point of local maxima and the value of local
Maximum is given by f(1) = 13- 6(1)2 + 9(1) + 15
= 1 - 6 + 9 + 15
= 19.
And at x = 3,f"(3) = 6 × 3 - 12 = 18 - 12 = 6 > 0
∴x = 3 is a point of local minima and the value of
local minimum is given by f (3) = 33- 6(3)2 + 9(3) + 15.
= 27 - 54 + 27 + 15.
= 15.
(vi)
A(vi)
We have,
At, extreme point, g'(x) = 0
Given, that x > 0, hence we have x = 2.
At, x = 2,
∴x = 2 is a point of local minima and value of local
Minimum is given by g(2) =
(vii)
A(vii)
Given,
At extreme points, g'(x) = 0.
At, x = 0,
∴x = 0 is a point of local maxima and value of local maximum is given by
Q4. Prove that the following functions do not have maxima or minima:
(i) f(x) = ex
A(i) We have, f(x) = ex
At, extreme points,
f(x) = 0
∴f(x) has with maximum or minima
(ii) g(x) = log x
A(ii)
We have, g(x) = log x,
At extreme points,
g(x) = 0
∴g(x) was value minima or maxima
(iii) h(x) = x3 + x2 + x + 1.
A(iii)
We have, h(x) = x3 + x2 + x + 1.
h(x) = 3x2 + 2x + 1
At extreme points,
h(x) = 0
Q5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) f(x) =x3 , x ∈ [– 2, 2]
A.(i) We have,
f(x) = x3 , x ∈ [– 2, 2].
f(x) = 3x2.
At, f(x) = 0
3x2 = 0
x = 0 <--[-2, 2].
We shall absolute the value of f at x = 0 and points of interval [ -2, 2]. So,
f(0) = 0
f(- 2) = (- 2)3 = 8
f(2) = 23 = 8.
∴ Absolute maximum value of f(x) = 8 at x = 2
and absolute minimum value of f(x) = -8 at x = -2.
(ii) f (x) = sin x + cos x , x ∈ [0, π]
A.(ii)
We have, f(x) = sin x + cos x , x ∈ [0, π]
f(x) = cos x - sin x.
atf(x) = 0
(iii) f(x) = 4x
A.(iii)
We have, f(x) = 4x
f(x) = 4 - x
atf(x) = 0
= 7.87.5
Hence, absolute maximum value of f(x) = 8 at x = 4
and absolute minimum value of f(x) = -10 at x = -2.
(iv) f(x) = (x - 1)2 + 3, x∈[ -3, 1]
A.(iv)
We have, f(x) = (x - 1)2 + 3, x∈[ -3, 1]
f(x) = 2(x -1)
atf(x) = 0
2(x - 1) = 0
x = 1∈ [ -3, 1]
∴f(1) = (1 - 1)2 + 3 = 3
f(- 3) = (- 3 - 1)2 + 3 = 16 + 3 = 1
∴ Absolute maximum value of f(x) = 19 at x = -3.
And absolute minimum value of f(x) = 3 at x = 1.
Q6. Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 72x – 18x2
A.6. We have, p(x) = 41 -f2x - 18x2.
P(x) = - 72 - 36x
P(x) = -36
At extreme point,
- 72 - 36x = 0
At x = - 2, p"(x) = - 36 < 0.
∴x = -2 is a point of local maximum and the value of local
Maximum is given by P(2) = 41 - 72(- 2) - 18(- 2)2
41 + 144 - 72 = 113 units.
Q7. Find both the maximum value and the minimum value of 3x4 – 8x3 + 12x2 – 48x + 25 on the interval [0, 3].
A7. We have, f(x) = 3x4- 8x3 + 12x2- 48x + 25, x ∈ [0, 3].
f(x) = 12x3- 24x2 + 24x - 48.
At f(x) = 0.
12x3- 24x2 + 24x - 48 = 0.
x3- 2x2 + 2x - 4 = 0
x2(x - 2) + 2(x - 2) = 0
(x - 2) + (x2 + 2) = 0
x = 2 ∈ [0, 3] or x =
∴f(x) = 3(2)4- 8(2)3 + 12(2)2- 4(2) + 25.
=48 - 64 + 48 - 96 + 25.
= -39.
f(0) =3(0)4- 8(0)3 + 12(0)2- 48(0) + 25.
= 25.
f(3) = 3(3)4- 8(3)3 + 12(3)2- 48(3) + 25.
= 243 - 216 + 108 - 144 + 25
= 16.
Maximum value of f(x) = 25 at x = 0.
and minimum value of f(x) = -39 at x = 2.
Q8. At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
A8. We have, f(x) = sin 2x, x ∈ [0, 2π],
f(x) = 2cos 2x.
At f(x) = 0.
2 cos 2x = 0
cos 2x = 0
= 1.
f(0) = sin 2(0) = sin 0 = 0
f(2π) = sin 2(2π) = sin 4π = 0
Hence, the points of maximum
Q9. What is the maximum value of the function sin x + cos x?
A9. We have, f(x) = sin x + cos x.
f(x) = cos x - sin x.
At f(x) = 0
cosx - sin x = 0
sinx = cos x
At
Find the maximum value of the same function in [–3, –1]
A.10. We have, f(x) =2x3- 24x + 107, x[1,3]
f(x) = 6x2- 24.
At f(x) = 0
6x2- 24= 0
x = ±2. -->x = 2 ∈[1, 3].
So, f(2) = 2(2)3- 24(2) + 107 = 16 - 48 + 107 = 75.
f(1) = 2(1)3- 24(1) + 107 = 2 - 24 + 107 = 85.
f(3) = 2(3)3- 24(3) + 107 = 54 - 72 + 107 = 89
∴ Maximum value of f(x) in interval [1, 3] is 89 at x = 3.
When x ∈ [ -3, -1]
From f(x) = 0
x = -2 ∈ [ -3, -1]
So, f(- 2) = 2(- 2)3- 24(- 2) + 107 = - 16 + 48 + 107 = 139.
f(- 3) = 2(- 3)3- 24(- 3) + 107 = - 54 + 72 + 107 = 125.
f(- 1) = 2(- 1)3- 24(- 1) + 107 = - 2 + 24 + 107 = 129.
∴ Maximum value of f(x) in interval [ -3, -1] is 139 at x = -2.
Q11. It is given that at x = 1, the function x4 – 62x2 + ax + 9 attains
its maximum value, on the interval [0, 2]. Find the value of a.
A.11. We have, f(x) = x4- 62x2 + ax + 9, x∈ [0, 2].
∴f(x) active its maxn value at x = 1∈ [0, 2]
∴f(1) = 0.
4(1)3- 124(1) + a = 0
∴a = 120
Q12. Find the maximum and minimum values of x + sin 2x on [0, 2π].
A.12. We have, f(x) = x + sin 2x ,x ∈ [0, 2π].
f(x) = 1 + 2cos 2x
At f(x) = 0
1 + 2 cos2x = 0
Hence,
Missing
At
= 1.05 + 0.87
= 1.92
At
= 1.23
At
=5.07.
At
= 5.25 - 0.87 = 4.38
At and points,
f(0) = 0 + sin2 × 0 = 0
f(2π) = 2π + sin 2 × 2π = 6.2 + 0 = 6.28
∴Maximum value of f(x) = 6.28 at x = 2π and
minimum value of f(x) = 0 at x= 0
Q13. Find two numbers whose sum is 24 and whose product is as large as possible.
A.13. Let ‘x’ and ‘y’ be the two number
Then, x + y = 24
Let ‘P’ be their product then,
P = xy = x (24 - x) = 24x -x2
P(x) = 24x -x2
At
24 - 2x = 0
So, P(12)
x = 12 is a point of local maxima
Hence, y = 24 - 12 = 12.
The uqdtwno (x, y) is (12, 12).
Q14. Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
A.14. We have, x + y = 60.where x, y > 0
x = 60 - y.
Let the product P = xy3 = (60 -y) y3 = 60y3-y4
= 4y2(45 -y)
At
As y > 0, y = 45
When, y > 45,
= ve < 0
Ad y < 45,
= (+ ve) > 0
∴p is maximum when y = 45 from + ve to- ve or y increases through 45.
So, x = 60 - y = 6Ø - 45 = 15.
Øx = 15 and y = 45.
Q15. Find two positive numbers x and y such that their sum is 35 and the product
x2 y5 is a maximum.
A.15. We have, x + y = 35.
y = 35 - x
Let the product, P =x2 y5
So,
= x (35 -x)4[ - 5x + (35 -x) 2]
= x (35 -x)4 [ - 5x + 70 - 2x]
= x (35 -x)4 (70 - 7x)
= 7x (35 -x)4 (10 -x)
At
As x is a (+) ve number we have only
x = 10, 35
And again (at x = 35) y = 35 = 0 but yis also a (+) ve number
we get, x = 10 (only)
whenx < 10,
and when x > 10,
Hence, x = 10 is a point of local maxima
So, y = 35 - 10 = 25
∴x = 10 and y = 25
Q16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum
A.16. Let, x and y be the two positive number
Then, x + y = 16 y = 16 - x
Let p be the sun of the cubes then
p = x3 + y3 = x3 + (16 -x)3 = x3 + (16)3-x3- 48x (16 -x)
p = 163 + 48x2- 76 8x
So,
At
96x - 768 = 0
∴at x = 8,
So, x = 8 is a point of local minima
So, y = 16 - 8 = 8
Hence, x = 8, y = 8
Q17. A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
A.17. Side of the tin square piece = 18 cm
Let x cm be the thought of the square to be cut from each corner.
The volume v of the box after cutting
= (18 - 2x)(18 - 2x) x x
= (18 - 2x)2x
= (324 + 4x2- 72x) x
= 4x3- 72x2 + 324x
So,
As
At x = 0, length of box = 18 - 2π9 = 18 - 18 = 0
Which is not possible
And at x = 3,
∴x = 3 is a point of maximum
Hence, ‘3’ cm (square) is to be cut from each side of the square
So that volume of box is maximum
Q18. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum?
A.18. Let ‘x’ cm be the length of side of the square to be cut off from the rectangular surface
Then, the volume v of the box is v = (45 - 2x)(24 - 2x) x
= 1080x - 138x2 + 4x3
So,
At,
At x = 18, breadth = 24 - 2(18) = 24 - 36 = -12 which is not possible
At,
Hence, x = 5 is the point of maximum
So, ‘5’ cm length of square seeds to be cut from each corner of the secthgle
Q19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
A.19. Let A.B.C.D.be the square increased in a given fixed circle with radius x
Let ‘x’ and ‘y’ be the length and breadth of the rectangle
∴x, y> 0
In ABC, right angle at B,
x2 + y2 = (2x)2
Q20. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
A.20. Let r and h be the radius and height of the cylinder
So, r, h > 0
The total surface area s is given by
S = 2πr(h + r) = content .
Then, the volume v of the cylinder
So,
For maximum,
Q21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
A21. The volume v of a cylinder of height h and radius r is
V = πr2h = 100
Let, s be the surface area then
S = 2r2hr(r + h) =
At,
At,
And
Q22. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
A.22. Let x and y in ‘m’ be the length of side of the square the radius of the circle respectily
Then, length of wire = perimeter of square + circumference of circle
The combine area A of the square and the circle is
A = x2 + πy2
So,
At,
At,
Hence, length of square =
and length of circle = 2πy
Q23. Prove that the volume of the largest cone that can be inscribed in a sphere
of radius R is
A.23. Let r and h be the radius and height of the one in scribed in the sphere of radius R.
Then, is ΔOBC, rt angle at B (h-r)2 + r2 = R2
Then the volume v of the cone is,
At
4Rh – 3h2 = 0.
h(4R – 3h) = 0.
h = 0 and
As h> 0,
At
and
Hence, Volume of Cone,
Q24. Show that the right circular cone of least curved surface and given volume
has an altitude equal to √2
A.24. Let r and h be the radius and height of the cone.
The volume V of the cone is.
And curve surface area S is
Q25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is
A.25. Let r, h, l and Ø be the radius, height, slant height and semi-vertical angle respectively of the cone. i.e., r, h, l>0.
Then, Volume V of the cone is
So,
.
Q26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is
A.26.
Q27. The point on the curve x2 = 2y which is nearest to the point (0, 5) is
(A) (2√2
A.27. The equation of the given curve is
x2 = 2y.
Let p(x, y) be a point on the curve.
The distance of p(x, y) from (0, 5) is say S is given by
Let z = s2 = x2 + y2 + 25 – 10y = 2y + y2 -10y + 25
z = y2 – 8y + 25
So,
At
At y = 4,
y = 4, is point of minimum distance.
So, x2 = 2y-->x2 = 2 × 4--> x2 = 8
Hence, the point of nearest distance are
Option (A) is correct.
Q28. For all real values of x, the minimum value of
(A) 0 (B) 1 (C) 3 (D)
A.28. We have,
At f(x) = 0.
x = 1 and x = -1.
At
At x = -1,
The maximum value of f(x)
Hence, option (D) is correct.
Q29. The maximum value of
(A)
A.29. We have,
At f(x) = 0.
2x – 1 = 0
=
Option (B) is
Hence maximum value of f(x) = at x = 1 and x = 0.
Option (c) is correct.
Class 12 Application of Derivatives Miscellaneous Exercise Solutions
Class 12 Math important reference books and preparation Tips
Maths Ncert Solutions class 12th Exam
Student Forum
Answered 2 days ago
Yes, Class 12 Math Relations and Functions includes all the key topics as per requirements for CBSE Board Exams. Relations and Functions has several exercises with plenty of practice problems to help students understand the concepts better. We have designed solutions in a simple and clear manner to
P
Beginner-Level 2

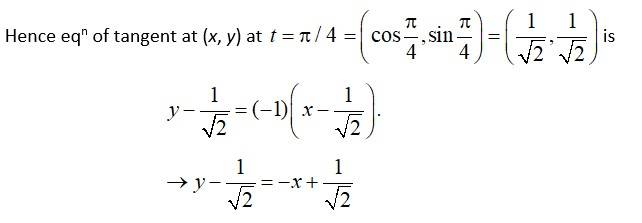
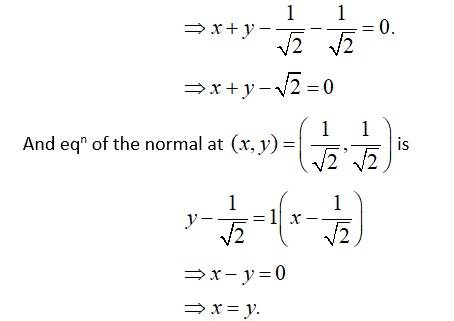


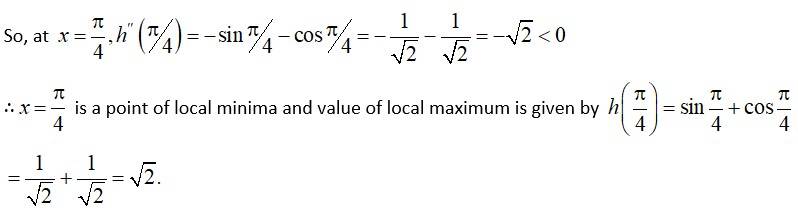

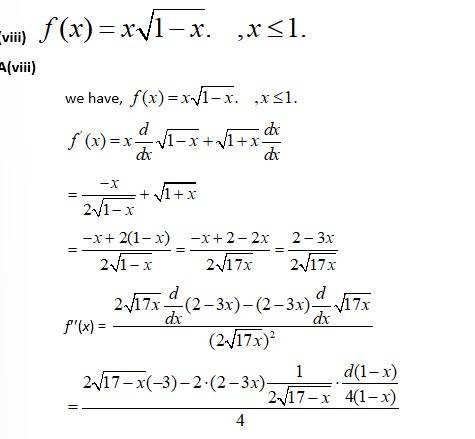

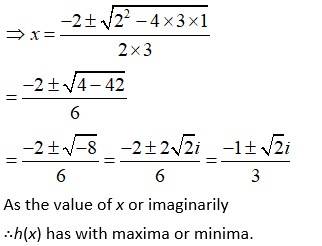
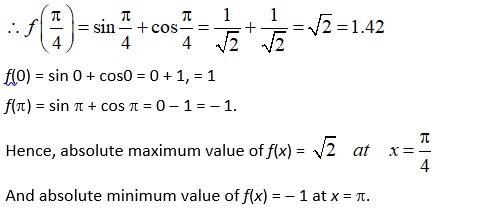
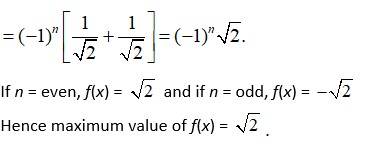
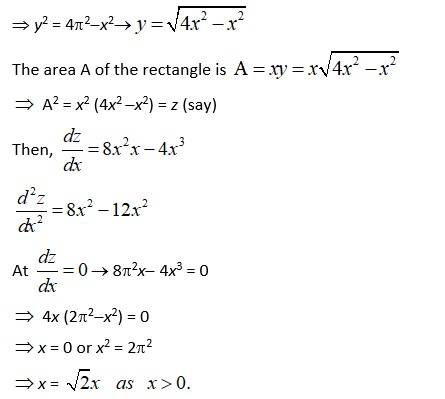
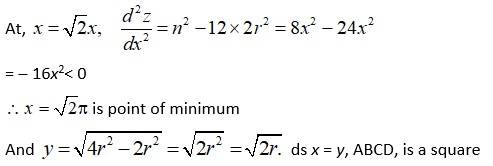
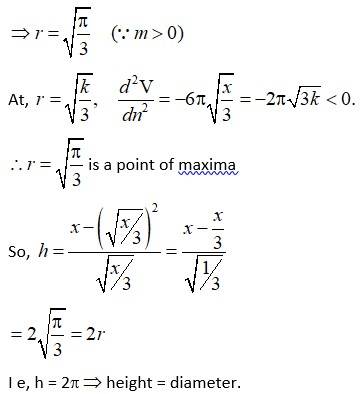





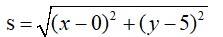
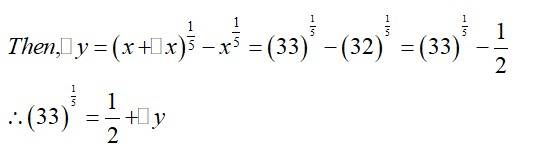

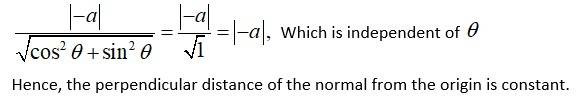






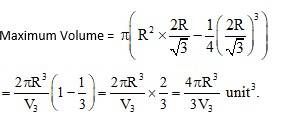

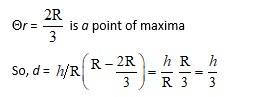

Will Class 12 Math Relation and Function NCERT Solutions be enough to prepare for the CBSE Boards exams?