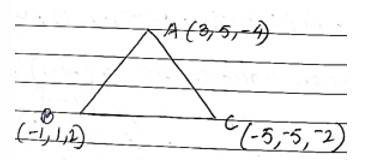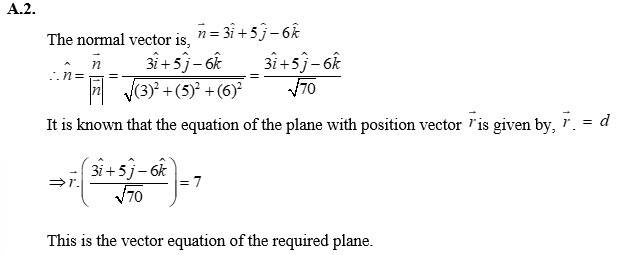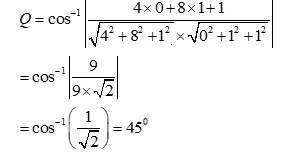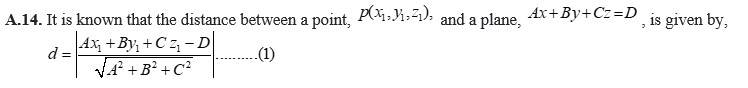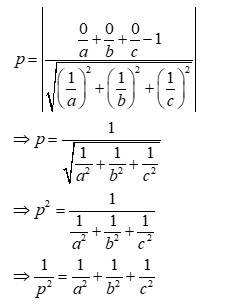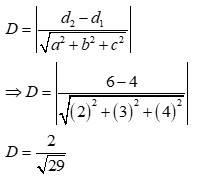Class 12 Chapter 11 Three-Dimensional Geometry NCERT Solutions: Students are provided with complete NCERT solutions for Class 12 Chapter 11 Three-Dimensional Geometry prepared by our experts in Shiksha. This chapter is immensely important for competitive exam aspirants due to its high weight. Class 12 Math Three-Dimensional Geometry focuses on many key topics such as the geometric representation of 3-dimensional space using vectors and Cartesian coordinates, the concept of direction cosines, and direction ratios of a line, providing methods to determine the equation of a line in vector and Cartesian forms. Class 12 Math Chapter 11 Three-Dimensional Geometry also focuses on the angle between two lines, two planes, or a line and a plane, along with the shortest distance between two skew lines.
Class 12 Math Three-Dimensional Geometry NCERT Solutions are helpful for both board and competitive exam students. Shiksha has compiled a complete Three-Dimensional Geometry NCERT Solutions of NCERT Textbook to help students. Students can access the complete Exercise-wise NCERT Class 12 chapter 11 Three-Dimensional Geometry solution PDF through the available link below.
Students must use the Three-Dimensional Geometry Class 12 Math Solution PDF conceptual understanding for CBSE Boards as well as other competitive exams such as BITSAT, CUSAT CAT, etc. Students should also check the Class 12 Chapter 10 Vector Algebra NCERT solutions, which can help better understand Three-Dimensional Geometry.
Class 12 Math Three-Dimensional Geometry explores many key topics such Equation of a line, and Plane in three-dimensional space. Students can access the complete Class 11 Math chapter-wise Solutions and Class 12 Chapter-wise Math solutions on Shiksha. For more information check below;
| Other Important Math Chapter Solutions | ||
|---|---|---|
| Class 12 Chapter 6 Application of Derivatives Solutions | Class 11 Chapter 8 Application of Integrals Solutions | Class 12 Chapter 9 Differential Equations Solutions |
- Three Dimensional Geometry Solutions and FAQs
- Class 12 Three Dimensional Geometry: Key Topics, Weightage and Important Formulae
- Class 12 Three Dimensional Geometry NCERT Solution PDF: Free PDF Download
- Class 12 Three Dimensional Geometry Exercise-wise Solutions
- Class 12 Three Dimensional Geometry Exercise 11.1 Solutions
- Class 12 Three Dimensional Geometry Exercise 11.2 Solutions
- Class 12 Three Dimensional Geometry Exercise 11.3 Solutions
- Class 12 Three Dimensional Geometry Miscellaneous Exercise Solutions
- Class 12 Math Preparation Tips and Recommended Books
Three Dimensional Geometry Solutions and FAQs
Exercise 11.1
Q4. Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
A.4. Given,
A(2,3,4), B(-1,-2,1), C(5,8,7)
Direction ratio of AB=
Where, a1=3, b1=-5, c1=-3
Direction ratio of BC=
Where, a2=6, b2=10, c2=6
Now,
Here, direction ratio of two-line segments are proportional.
So, A, B, C are collinear.
Q5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, − 4), (− 1, 1, 2) and (− 5, − 5, − 2)
A.5. The vertices of U ABC are A(3,5,-4), B(-1,1,2) and C(-5,-5,-2)
Direction ratio of side AB
Direction cosine of AB,
Example 11.2
Q1. Show that the three lines with direction cosines are mutually perpendicular.
A.1. Two lines with direction cosines l, m, n and l2, m2, n2 are perpendicular to each other, if .
Now, for the 3 lines with direction cosine,
Hence, the lines are perpendicular.
For lines with direction cosines,
Hence, these lines are perpendicular.
For the lines with direction cosines,
Hence, these lines are perpendicular.
Therefore, all the lines are perpendicular.
Q2. Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
A2. Let AB be the line joining the points and and CD be the line joining the point and .
The direction ratios, a, b, c of AB are
The direction ratios of CD are
AB and CD will be perpendicular to each other, if
Therefore, AB and CD are perpendicular to each other.
Q3. Show that the line through points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (−1, −2, 1), (1, 2, 5).
A.3. Let AB be the line through the point and and CD be line through the point and
Direction cosine, of AB are
Direction cosine, of CD are
AB will be parallel to CD only
If
Here,
Therefore, AB is parallel to CD.
Q4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
A.4. Given,
The line passes through the point .
Position vector of A,
Let
The line which passes through point and parallel to is given by,
, where is constant
Q5. Find the equation of the line in vector and in Cartesian form that passes through the point with position vector and is in the direction
A5. The line passes through the point with position vector,
The given vector:
The line which passes through a point with position vector and parallel to is given by,
This is required equation of the line in vector form.
Now,
Let
Comparing the coefficient to eliminate ,
Q6. Find the Cartesian equation of the line which passes through the point (−2, 4, −5) and parallel to the line given by
A.6. Given,
The point .
The Cartesian equation of a line through a point and having direction ratios a, b, c is
Now, given that
is parallel
to point
Here, the point is and the direction ratio is given by
The required Cartesian equation is
Q7. The Cartesian equation of a line is Write its vector form.
A.7. Given,
Cartesian equation,
The given line passes through the point
i.e. position vector of
Direction ratio are 3, 7 and 2.
Thus, the required line passes through the point and is parallel to the vector .
Let be the position vector of any point on the line, then the vector equation of the line is given by,
Q8. Find the vector and Cartesian equations of the line that passes through the origin and (5, −2, 3).
A.8. The required line passes through the origin. Therefore, its position vector is given by,
The direction ratios of the line through origin and are
The line is parallel to the vector given by the equation,
The equation of the line in vector form through a point with position vector and parallel to is,
The equation of the line through the point and direction ratios is given by,
Therefore, the equation of the required line in the Cartesian form is
Q9. Find vector and Cartesian equations of the line that passes through the points
A.9. Let the line passing through the points, P (3, −2, −5) and Q (3, −2, 6), be PQ.
Since PQ passes through P (3, −2, −5), its position vector is given by,
The direction ratios of PQ are given by,
The equation of the vector in the direction of PQ is
The equation of PQ in vector form is given by,
The equation of PQ in Cartesian form is
i.e,
Q10. Find the angle between the following pairs of lines:
A.10.
(i) Let Q be the angle between the given lines.
The angle between the given pairs of lines is given by,
The given lines are parallel to the vectors, , respectively.
Q11. Find the angle between the following pair of lines
A.11. (i) Let and be the vectors parallel to the pair of lines, , respectively.
If Q is the angle between the given pair of lines, then
Q12. Find the values of p so that the lines are at right angles.
A.12.
The standard form of a pair of Cartesian lines is;
So,
Comparing (1) and (2) we get
Now, both the lines are at right angles
So,
The value of is
Q13. Show that the lines are perpendicular to each other.
A.13.
Direction ratios of given lines are (7,-5,1) and (1,2,3).
i.e.,
Now,
These two lines are perpendicular to each other.
Q14. Find the shortest distance between the lines
A.14.
Solution. Comparing (1) and (2) with and respectively.
We get,
Therefore,
Q15. Find the shortest distance between the lines .
A.15.
Shortest distance between two lines is given by,
Then,
Q16. Find the shortest distance between the lines whose vector equations are
A.16.
Here, comparing (1) and (2) with and , we have
Q17. Find the shortest distance between the lines whose vector equations are
A.17.
Here,
EXERCISE 11.3
Q1. In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
A.1. (a) The equation of the plane is
The direction ratios of normal are
Dividing both sides of equation (1) by 1, we obtain
This is of the form , where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin is 2 units.
(b)
The direction ratios of normal are 1, 1, and 1.
Q2. Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
Q3. Find the Cartesian equation of the following planes:
A.3. (a) It is given that equation of the plane is
For any arbitrary point on the plane, position vector I s given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(b)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(c)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the given plane.
Q4. In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin:
A.4. (a) Let the coordinates of the foot of perpendicular P from the origin to the plane be
Q5. Find the vector and Cartesian equations of the planes
(a) that passes through the point and the normal to the plane is .
(b) that passes through the point and the normal vector to the plane is .
A.5. (a) The position vector of point is
The normal vector N perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
(b) The position vector of the point is
The normal vector perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
Q6. Find the equations of the planes that passes through three points:
(a) (1, 1, −1), (6, 4, −5), (−4, −2, 3)
(b) (1, 1, 0), (1, 2, 1), (−2, 2, −1)
A.6. We know that through three collinear points i.e., through a straight line, we can pass an infinite number of planes.
(a) The given points are
Since are collinear points, there will be infinite number of planes passing through the given points.
(b) The given points are
Therefore, a plane will pass through the points A, B, and C.
It is known that the equation of the plane through the points, , is
This is the Cartesian equation of the required plane.
Q7. Find the intercepts cut off by the plane
A.7.
Dividing both sides of equation (1) by 5, we obtain
It is known that the equation of a plane in intercept form is , where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively.
Therefore, for the given equation,
Thus, the intercepts cut off by the plane are
Q8. Find the equation of the plane with intercept 3 on the y- axis and parallel to ZOX plane.
A.8. The equation of the plane ZOX is
y = 0
Any plane parallel to it is of the form, y = a
Since the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane is y = 3
Q9. Find the equation of the plane through the intersection of the planes and the point
A.9. The equation of any plane through the intersection of the planes,
is
The plane passes through the point Therefore, this point will satisfy equation (1).
Substituting in equation (1), we obtain
Q10. Find the vector equation of the plane passing through the intersection of the planes and through the point
A.10. The equations of the planes are
The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,
The plane passes through the point (2, 1, 3). Therefore, its position vector is given by,
Substituting in equation (3), we obtain
Substituting in equation (3), we obtain
This is the vector equation of the required plane.
Q11. Find the equation of the plane through the line of intersection of the planes which is perpendicular to the plane
A.11. The equation of the plane through the intersection of the planes, , is
The direction ratios, of this plane are
The plane in equation (1) is perpendicular to
Its direction ratios, are .
Since the planes are perpendicular,
Substituting in equation (1), we obtain
This is the required equation of the plane.
Q12. Find the angle between the planes whose vector equations are
A.12. The equations of the given planes are
It is known that if n1 and n2 are normal to the planes, then the angle between them, Q, is given by,
Q13. In the following cases, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angle between them.
A.13. The direction ratios of normal to the plane, , are and
The angle between is given by,
(b) The equations of the planes are
Thus, the given planes are perpendicular to each other.
(c) The equations of the given planes are
Here,
Thus, the given planes are not perpendicular to each other.
Thus, the given planes are parallel to each other
(d) The equations of the planes are and
Thus, the given lines are parallel to each other
(e) The equations of the given planes are
Therefore, the given lines are not perpendicular to each other.
Therefore, the given lines are not parallel to each other.
The angle between the planes is given by,
Q14. In the following cases find the distances of each of the given points from the corresponding given plane:
Miscellaneous Exercise
Q1. Show that the line joining the origin to the point is perpendicular to the line determined by the points
A.1. Let OA be the line joining the origin, and the point,
Also, let BC be the line joining the points,
The direction ratios of
OA is perpendicular to
Thus, OA is perpendicular to BC.
Q2. If are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are
A.2. It is given that are the direction cosines of two mutually perpendicular lines. Therefore,
Let be the direction cosines of the line which is perpendicular to the line with direction cosines
are the direction cosines of the line.
It is known that,
Substituting the values from equations (5) and (6) in equation (4), we obtain
Thus, the direction cosines of the required line are
Q3. Find the angle between the lines whose direction ratios are
A.3. The angle Q between the lines with direction cosines,
is given by,
Q4. Find the equation of the line parallel to x-axis and passing through the origin.
A.4. The line parallel to x-axis and passing through the origin is x-axis itself.
Let A be a point on x-axis. Therefore, the coordinates of A are given by Direction ratios of
The equation of OA is given by,
Thus, the equation of line parallel to x-axis and passing through origin is
Q5. If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (−4, 3, −6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
A.5. The coordinates of and
respectively.
The direction ratios of
The direction ratios of
It can be seen that,
Therefore, AB is parallel to CD.
Thus, the angle between
Q6. .If the lines are perpendicular, find the value of k
A.6. The direction of ratios of the lines, , are respectively.
It is known that two lines with direction ratios, , are perpendicular, if
Therefore, for k= -10/7, the given lines are perpendicular to each other.
Q7. Find the vector equation of the line passing through and perpendicular to the plane
A.7. The position vector of the point is
The direction ratios of the normal to the plane, , are and the normal vector is
The equation of a line passing through a point and perpendicular to the given plane is given by,
Q8. .Find the equation of the plane passing through and parallel to the plane
A.8. Any plane parallel to the plane, , is of the form
The plane passes through the point (a, b, c). Therefore, the position vector of this point is
Therefore, equation (1) becomes
Substituting in equation (1), we obtain
This is the vector equation of the required plane.
Substituting in equation (2), we obtain
Q10. Find the coordinates of the point where the line through crosses the YZ-plane.
A.10. It is known that the equation of the line passing through the points, is
The line passing through the points, is given by,
Any point on the line is of the form
The equation of
Since the line passes through YZ-plane,
Therefore, the required point is .
Q11. Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX-plane.
A.11. It is known that the equation of the line passing through the points, is
The line passing through the points, is given by,
Any point on the line is of the form
Since the line passes through ZX-plane,
Therefore, the required point is
Q12. Find the coordinates of the point where the line through
crosses the plane
A.12. It is known that the equation of the line through the points, , is
Since the line passes through the points, , its equation is given by,
Therefore, any point on the line is of the form
This point lies on the plane,
Hence, the coordinates of the required point are
Q13. Find the equation of the plane passing through the point and perpendicular to each of the planes
A.13. The equation of the plane passing through the point where, a, b, c are the direction ratios of normal to the plane.
It is known that two planes, are perpendicular, if
Plane (1) is perpendicular to the plane,
Also, plane (1) is perpendicular to the plane,
From equations (2) and (3), we obtain
Substituting the values of a, b, and c in equation (1), we obtain
This is the required equation of the plane.
Q14. If the points be equidistant from the plane then find the value of p
A.14. The position vector through the point is
Similarly, the position vector through the point is
The equation of the given plane is
It is known that the perpendicular distance between a point whose position vector is and the plane, is given by,
Q15. Find the equation of the plane passing through the line of intersection of the planes and parallel to x - axis.
A.15. Equation of one plane is
The equation of any plane passing through the line of intersection of these planes is
Its direction ratios are (2λ + 1), (3λ + 1), and (1 − λ).
The required plane is parallel to x-axis. Therefore, its normal is perpendicular to x-axis.
The direction ratios of x-axis are 1, 0, and 0.
Substituting λ = -1/2 in equation (1), we obtain
Therefore, its Cartesian equation is y − 3z + 6 = 0
This is the equation of the required plane.
Q16. If O be the origin and the coordinates of P be (1, 2, −3), then find the equation of the plane passing through P and perpendicular to OP.
A.16. The coordinates of the points, O and P, are (0, 0, 0) and (1, 2, −3) respectively.
Therefore, the direction ratios of OP are (1 − 0) = 1, (2 − 0) = 2, and (−3 − 0) = −3
It is known that the equation of the plane passing through the point (x1, y1 z1) is
where, a, b, and c are the direction ratios of normal.
Here, the direction ratios of normal are 1, 2, and −3 and the point P is (1, 2, −3).
Thus, the equation of the required plane is
Q17. Find the equation of the plane which contains the line of intersection of the planes and which is perpendicular to the plane .
A.17. The equations of the given planes are
The equation of the plane passing through the line intersection of the plane given in equation (1) and equation (2) is
The plane in equation (3) is perpendicular to the plane,
Substituting λ = 7/19 in equation (3), we obtain
This is the vector equation of the required plane.
The Cartesian equation of this plane can be obtained by substituting in equation (3).
The equation of the given line is
.....(1)
The equation of the given plane is
.......(2)
Substituting the value of from equation (1) in equation (2), we obtain
Substituting this value in equation (1), we obtain the equation of the line as
This means that the position vector of the point of intersection of the line and the plane is
This shows that the point of intersection of the given line and plane is given by the coordinates, (2, −1, 2). The point is (−1, −5, −10).
The distance d between the points, (2, −1, 2) and (−1, −5, −10), is
Q19. Find the vector equation of the line passing through (1, 2, 3) and parallel to the plane and
A.19. Let the required line be parallel to vector given by,
The position vector of the point (1, 2, 3) is
The equation of line passing through (1, 2, 3) and parallel to is given by,
The equations of the given planes are
The line in equation (1) and plane in equation (2) are parallel. Therefore, the normal to the plane of equation (2) and the given line are perpendicular.
Similarly,
From equations (4) and (5), we obtain
Therefore, the direction ratios of are −3, 5, and 4.
Substituting the value of in equation (1), we obtain
This is the equation of the required line.
Q20. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:
and
A.20. Let the required line be parallel to the vector given by,
The position vector of the point (1, 2, − 4) is
The equation of the line passing through (1, 2, −4) and parallel to vector is
The equations of the lines are
Line (1) and line (2) are perpendicular to each other.
Also, line (1) and line (3) are perpendicular to each other.
From equations (4) and (5), we obtain
Direction ratios of are 2, 3, and 6.
Substituting in equation (1), we obtain
This is the equation of the required line.
Q21. Prove that if a plane has the intercepts a,b,c and is at a distance of P units from the origin, then
A.21. The equation of a plane having intercepts a, b, c with x, y, and z axes respectively is given by,
The distance (p) of the plane from the origin is given by,
choose the correct answer in Exercise Q. 22 and 23.
Q22. Distance between the two planes: is
(A) 2 units (B) 4 units (C) 8 units (D) 2/√29 units
A.22. The equations of the planes are
It can be seen that the given planes are parallel.
It is known that the distance between two parallel planes, is given by,
Thus, the distance between the lines is 2/√29 units.
Hence, the correct answer is D.
Q23. The planes: are
(A) Perpendicular (B) Parallel (C) intersect y-axis
(D) passes through (0,0,5/4)
A.23. The equations of the planes are
It can be seen that,
Therefore, the given planes are parallel.
Hence, the correct answer is B.
Class 12 Three Dimensional Geometry: Key Topics, Weightage and Important Formulae
Class 12 Chapter 11 Three-Dimensional Geometry carries very good weightage around CBSE 12-14 marks in CBSE Boards. Generally, 1-2 questions are asked from Three-Dimensional Geometry, including both theory and application-based problems. Class 12 Chapter 11 Three-Dimensional Geometry is also important, as it has moderate weightage approximately 4-8 marks in JEE Mains. Vector Algebra and Three-Dimensional Theory combined include very important topics such as vector addition, vector multiplication; cross, and dot product, that are useful beyond mathematics. Students can check the key topics and important formulae below;
Class 12 Chapter 11 Three-Dimensional Geometry Key Topic
Students can check Key Topics below;
- Direction Cosines and Direction Ratios: Definition, Relationship between direction cosines
- Equation & Vector form of a Line in 3D
- Equation: Plane passing through a point and normal to a vector, and through three points.
- Angle between Lines, Planes, and Line-Plane
- Shortest Distance between two skew lines, and a point from a plane.
- Intersection of Lines and Planes, Point of intersection between a line and a plane.
- Condition for coplanarity of two lines.
Check out Chapter 11 Three Dimensional Geometry Dropped Topics – 11.2.1 Relation between the Direction Cosines of a Line, 11.3.2 Equation of a Line Passing through Two Given Points, Ques. 8–9 (Exercise 11.2), 11.6 Plane, 11.7 Coplanarity of Two Lines, 11.8 Angle between Two Planes, 11.9 Distance of a Point from a Line, 11.10 Angle between a Line and a Plane, Ques. 1, 2, 5, 7–8, 10–19, 21–23 (Miscellaneous Exercise), Page 500-501 Summary Points 13, 20–24, Page 502-503 Full Pages
Class 12 Chapter 11 Three-Dimensional Geometry Important Formulae for CBSE and Competitive Exams
-
Direction Cosines Relationship
-
Equation of a Line
- Vector form:
- Cartesian form:
-
Equation of a Plane
- General form:
- Vector form:
-
Angle between Two Lines
-
Angle between Two Planes
-
Distance of a Point from a Plane
-
Shortest Distance Between Two Skew Lines
-
Condition for Coplanarity of Two Lines
Class 12 Three Dimensional Geometry NCERT Solution PDF: Free PDF Download
Shiksha has compiled the complete exercise-wise solution of the Class 12 Three-Dimensional Geometry NCERT PDF in one place prepared by our experts. Students can use Class 12 Three-Dimensional Geometry NCERT Solutions to build a strong conceptual understanding of Vector and 3D geometry, which is equally useful for Physics. The Three-Dimensional Geometry Class 12 NCERT Solution PDF will be useful for both CBSE boards and competitive exams aspirants; JEE Main, CUSAT CAT, GUJCET, etc... Students can access the Three-Dimensional Geometry Class 12 Solutions pdf download for free below;
Class 12 Math Chapter 10 Vector Solution PDF: Free PDF Download
Class 12 Three Dimensional Geometry Exercise-wise Solutions
Chapter 11 Three-dimensional geometry involves concepts such as Direction Cosines and Direction Ratios, the Equation of a Line, the Angle between a line and a plane, and others. Students must understand these topics to excel in board exams and competitive entrance tests.
Class 12 Three Dimensional Geometry Exercise 11.1 Solutions
Class 12 Three-Dimensional Geometry Exercise 11.1 Solutions
Q4. Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
A.4. Given,
A(2,3,4), B(-1,-2,1), C(5,8,7)
Direction ratio of AB=
Where, a1=3, b1=-5, c1=-3
Direction ratio of BC=
Where, a2=6, b2=10, c2=6
Now,
Here, direction ratio of two-line segments are proportional.
So, A, B, C are collinear.
Q5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, − 4), (− 1, 1, 2) and (− 5, − 5, − 2)
A.5. The vertices of U ABC are A(3,5,-4), B(-1,1,2) and C(-5,-5,-2)
Direction ratio of side AB
Direction cosine of AB,
Class 12 Three Dimensional Geometry Exercise 11.2 Solutions
Class 12 Three-Dimensional Geometry 11.2 Exercise Solutions
Q1. Show that the three lines with direction cosines are mutually perpendicular.
A.1. Two lines with direction cosines l, m, n and l2, m2, n2 are perpendicular to each other, if .
Now, for the 3 lines with direction cosine,
Hence, the lines are perpendicular.
For lines with direction cosines,
Hence, these lines are perpendicular.
For the lines with direction cosines,
Hence, these lines are perpendicular.
Therefore, all the lines are perpendicular.
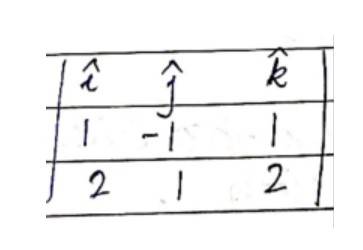
Q2. Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
A2. Let AB be the line joining the points and and CD be the line joining the point and .
The direction ratios, a, b, c of AB are
The direction ratios of CD are
AB and CD will be perpendicular to each other, if
Therefore, AB and CD are perpendicular to each other.
Q3. Show that the line through points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (−1, −2, 1), (1, 2, 5).
A.3. Let AB be the line through the point and and CD be line through the point and
Direction cosine, of AB are
Direction cosine, of CD are
AB will be parallel to CD only
If
Here,
Therefore, AB is parallel to CD.
Q4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
A.4. Given,
The line passes through the point .
Position vector of A,
Let
The line which passes through point and parallel to is given by,
, where is constant
Q5. Find the equation of the line in vector and in Cartesian form that passes through the point with position vector and is in the direction
A5. The line passes through the point with position vector,
The given vector:
The line which passes through a point with position vector and parallel to is given by,
This is required equation of the line in vector form.
Now,
Let
Comparing the coefficient to eliminate ,
Q6. Find the Cartesian equation of the line which passes through the point (−2, 4, −5) and parallel to the line given by
A.6. Given,
The point .
The Cartesian equation of a line through a point and having direction ratios a, b, c is
Now, given that
is parallel
to point
Here, the point is and the direction ratio is given by
The required Cartesian equation is
Q7. The Cartesian equation of a line is Write its vector form.
A.7. Given,
Cartesian equation,
The given line passes through the point
i.e. position vector of
Direction ratio are 3, 7 and 2.
Thus, the required line passes through the point and is parallel to the vector .
Let be the position vector of any point on the line, then the vector equation of the line is given by,
Q8. Find the vector and Cartesian equations of the line that passes through the origin and (5, −2, 3).
A.8. The required line passes through the origin. Therefore, its position vector is given by,
The direction ratios of the line through origin and are
The line is parallel to the vector given by the equation,
The equation of the line in vector form through a point with position vector and parallel to is,
The equation of the line through the point and direction ratios is given by,
Therefore, the equation of the required line in the Cartesian form is
Q9. Find vector and Cartesian equations of the line that passes through the points
A.9. Let the line passing through the points, P (3, −2, −5) and Q (3, −2, 6), be PQ.
Since PQ passes through P (3, −2, −5), its position vector is given by,
The direction ratios of PQ are given by,
The equation of the vector in the direction of PQ is
The equation of PQ in vector form is given by,
The equation of PQ in Cartesian form is
i.e,
Q10. Find the angle between the following pairs of lines:
A.10.
(i) Let Q be the angle between the given lines.
The angle between the given pairs of lines is given by,
The given lines are parallel to the vectors, , respectively.
Q11. Find the angle between the following pair of lines
A.11. (i) Let and be the vectors parallel to the pair of lines, , respectively.
If Q is the angle between the given pair of lines, then
Q12. Find the values of p so that the lines are at right angles.
A.12.
The standard form of a pair of Cartesian lines is;
So,
Comparing (1) and (2) we get
Now, both the lines are at right angles
So,
The value of is
Q13. Show that the lines are perpendicular to each other.
A.13.
Direction ratios of given lines are (7,-5,1) and (1,2,3).
i.e.,
Now,
These two lines are perpendicular to each other.
Q14. Find the shortest distance between the lines
A.14.
Solution. Comparing (1) and (2) with and respectively.
We get,
Therefore,
Q15. Find the shortest distance between the lines .
A.15.
Shortest distance between two lines is given by,
Then,
Q16. Find the shortest distance between the lines whose vector equations are
A.16.
Here, comparing (1) and (2) with and , we have
Q17. Find the shortest distance between the lines whose vector equations are
A.17.
Here,
Class 12 Three Dimensional Geometry Exercise 11.3 Solutions
Class 12 Three-Dimensional Geometry Exercise 11.3 Solutions
Q1. In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
A.1. (a) The equation of the plane is
The direction ratios of normal are
Dividing both sides of equation (1) by 1, we obtain
This is of the form , where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin is 2 units.
(b)
The direction ratios of normal are 1, 1, and 1.
Q2. Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
Q3. Find the Cartesian equation of the following planes:
A.3. (a) It is given that equation of the plane is
For any arbitrary point on the plane, position vector I s given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(b)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(c)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the given plane.
Q4. In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin:
A.4. (a) Let the coordinates of the foot of perpendicular P from the origin to the plane be
Q5. Find the vector and Cartesian equations of the planes
(a) that passes through the point and the normal to the plane is .
(b) that passes through the point and the normal vector to the plane is .
A.5. (a) The position vector of point is
The normal vector N perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
(b) The position vector of the point is
The normal vector perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
Q6. Find the equations of the planes that passes through three points:
(a) (1, 1, −1), (6, 4, −5), (−4, −2, 3)
(b) (1, 1, 0), (1, 2, 1), (−2, 2, −1)
A.6. We know that through three collinear points i.e., through a straight line, we can pass an infinite number of planes.
(a) The given points are
Since are collinear points, there will be infinite number of planes passing through the given points.
(b) The given points are
Therefore, a plane will pass through the points A, B, and C.
It is known that the equation of the plane through the points, , is
This is the Cartesian equation of the required plane.
Q7. Find the intercepts cut off by the plane
A.7.
Dividing both sides of equation (1) by 5, we obtain
It is known that the equation of a plane in intercept form is , where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively.
Therefore, for the given equation,
Thus, the intercepts cut off by the plane are
Q8. Find the equation of the plane with intercept 3 on the y- axis and parallel to ZOX plane.
A.8. The equation of the plane ZOX is
y = 0
Any plane parallel to it is of the form, y = a
Since the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane is y = 3
Q9. Find the equation of the plane through the intersection of the planes and the point
A.9. The equation of any plane through the intersection of the planes,
is
The plane passes through the point Therefore, this point will satisfy equation (1).
Substituting in equation (1), we obtain
Q10. Find the vector equation of the plane passing through the intersection of the planes and through the point
A.10. The equations of the planes are
The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,
The plane passes through the point (2, 1, 3). Therefore, its position vector is given by,
Substituting in equation (3), we obtain
Substituting in equation (3), we obtain
This is the vector equation of the required plane.
Q11. Find the equation of the plane through the line of intersection of the planes which is perpendicular to the plane
A.11. The equation of the plane through the intersection of the planes, , is
The direction ratios, of this plane are
The plane in equation (1) is perpendicular to
Its direction ratios, are .
Since the planes are perpendicular,
Substituting in equation (1), we obtain
This is the required equation of the plane.
Q12. Find the angle between the planes whose vector equations are
A.12. The equations of the given planes are
It is known that if n1 and n2 are normal to the planes, then the angle between them, Q, is given by,
Q13. In the following cases, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angle between them.
A.13. The direction ratios of normal to the plane, , are and
The angle between is given by,
(b) The equations of the planes are
Thus, the given planes are perpendicular to each other.
(c) The equations of the given planes are
Here,
Thus, the given planes are not perpendicular to each other.
Thus, the given planes are parallel to each other
(d) The equations of the planes are and
Thus, the given lines are parallel to each other
(e) The equations of the given planes are
Therefore, the given lines are not perpendicular to each other.
Therefore, the given lines are not parallel to each other.
The angle between the planes is given by,
Q14. In the following cases find the distances of each of the given points from the corresponding given plane:
Class 12 Three Dimensional Geometry Miscellaneous Exercise Solutions
Class 12 Math Preparation Tips and Recommended Books
Maths Ncert Solutions class 12th Exam