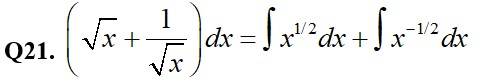Ex.7.1
Find an anti-derivative (or integral) of the following functions by the method of inspection.
Q1.
A.1.
Therefore, an anti-derivative of
Q2.
A.2.
Therefore, an anti-derivative of
Q3.
A.3.
Therefore, an anti-derivative of
Q4.
A.4.
Therefore, an anti-derivative of
.
Q5.
A.5.
Therefore, an anti-derivative of
Find the following integrals in Exercises 6 to 20:
Q6.
A.6.
=
Q7.
A.7.
Q8.
A.8.
Q9.
A.9.
Q11.
A.11.
A.12.
Q13.
A.13.
Q14.
A.14.
c
Q15.
A.15.
Q.16.
A.16.
Q.17.
A.17.
Q18.
A.18.
Q19.
A.19.
Q20.
A.20.
Choose the correct answer in Exercises 21 and 22.
A.21.
⸫ The correct Answer is (C)
Q.22.
A.22.
Now,
Therefore, correct answer is A.
Ex.7.2
Integrate the functions in Exercises 1 to 37:
Q1.
1.
Q2.
A.2.
Q3.
A.3.
Q4.
A.4.
![]()
Q5.
A.5.
Q6. √ax + b
A.6.
Q7.
A.7.
A.8.
A.10.
Q12.
A.12.
Q13.
A.13.
Q14.
A.14.
Q15.
A.15.
Q16.
A.16.
Q17.
A.17.
Q18.
A.18.
Q19.
A.19. Dividing both numerator and denominator by ex, we get
Q20.
A.20.
Q21.
A.21.
Q22.
A.22.
Q24.
A.24.
Q25.
A.25.
Q29.
A.29.
Q30.
A.30.
Q31.
A.31.
Q32.
A.32.
Q33.
A.33.
Q35.
A.35.
Q36.
A.36.
Q37.
A.37.
From (1), we get
Choose the correct answer in Exercises 38 and 39.
Q38.
A.38.
Therefore, the correct answer is (D)
Q39.
A.39.
Therefore, the correct answer is B.
Ex. 7.3
Find the integrals of the functions in Exercises 1 to 22:
Q1.
A.1.
Q2.
A2.
Q3.
A.3.
Q4.
A.4.
Q5.
A.5.
Q6.
A.6.
Q7.
A.7.
Q8.
A.8.
Q9.
A.9.
Q10.
A.10.
Q11.
A.11.
Q12.
A.12.
Q13.
A.13.
Q14.
A.14.
Q15.
A.15.
Q16.
A.16.
I
Q17.
A.17.
Q18.
A.18.
Q19.
A.19.
Q20.
A.20.
Q21.
A.21.
Q22.
A.22.
Q23.
A.23.
Q24.
A.24.
Ex.7.4
Integrate the functions in Exercises 1 to 23.
Q1.
A.1.
Q5.
A.5.
Q6.
A.6.
Q11.
A.11.