
Class 12 Chapter 3 Matrices NCERT Solutions: Students can find complete class 12 Matrices solutions prepared by our experts in Shiksha. Class 12 Chapter 3 Matrices is an important chapter because of its weightage in board and competitive exams. The concepts of the Matrices chapter are used in solving linear equations in coordinate geometry, linear algebra, and more.
The concepts of Matrices were developed in an attempt to find short and simple ways of solving the system of linear equations. Matrices are used as a representation of the coefficients in a system of linear equations (in the form of data/ table). Tools of Matrices are used in many disciplines such as economics, mechanics, modern psychology, genetics, and others.
We have provided Class 12 Matrices NCERT Solutions with detailed explanations, covering each concept. Students must check out the complete Class 11 Math chapter-wise Solutions and Class 12 Chapter-wise Math solutions available on Shiksha. Students can also download the complete Exercise-wise solution of Matrices Class 12 NCERT PDF for free from this page.
Students must download the Class 12 Math Matrices Solution PDF and use it to strengthen their concepts for Boards and other entrance exams such as JEE, COMEDK etc. Students can read the article below for complete information on the Class 12 NCERT Matrices chapter such as important formulae, weightage, exercise-wise solutions, and more;
| Related Important Math Chapter Solutions | ||
|---|---|---|
| Class 12 Chapter 10 Vector Algebra | Class 11 Chapter 12 Three-Dimensional Geometry | Class 12 Chapter 4 Determinants |
- Class 12 Math Chapter 3 Matrices: Key Topics, Weightage & Important Formulae
- Class 12 Math Chapter 3 Matrices Solution PDF: Free Download
- Class 12 Math Chapter 3 Matrices Exercise-wise Solutions
- Class 12 Math Chapter 3 Matrices Exercise 3.1 Solutions
- Class 12 Math Chapter 3 Matrices Exercise 3.2 Solutions
- Class 12 Math Chapter 3 Matrices Exercise 3.3 Solutions
- Class 12 Math Chapter 3 Matrices Exercise 3.4 Solutions
- Class 12 Math Chapter 3 Matrices Miscellaneous Exercise Solutions
- Class 12 Math important reference books and preparation Tips
Class 12 Math Chapter 3 Matrices: Key Topics, Weightage & Important Formulae
The Class 12 Chapter 3 Matrices typically have 6-8 marks weightage in the CBSE Class 12 Board Exams. Matrices are also a very important chapter for competitive exams for their direct weightage moreover its applications in solving linear equation systems in geometry, linear algebra, vector algebra, and more. Check the Key Topics discussed in Matrices Class 12 Solutions below;
Class 12 Matrices Key Topics
- Fundamentals of Matrices: Matrices are defined as an ordered rectangular array of numbers or functions. The numbers or functions are called the elements/ entries of the matrix. basic of Matrices are discussed.
- Types of Matrices: Row Matrix, Column Matrix, Square Matrix, Diagonal Matrix, Scalar Matrix, Identity Matrix, Zero/Null Matrix, Symmetric and Skew-Symmetric Matrices.
- Operations on Matrices: Addition and Subtraction, Scalar Multiplication, Matrix/ Vector Multiplication, Transpose of a Matrix.
- Other Important Concepts: Properties of Matrix Operations, Determinants and Inverses
- Applications of Matrices: Solving linear equations system using matrices.
**Check out Dropped Topics of Class 12 Chapter 3 Matrices – 3.7 Elementary Operations (Transformation) of a Matrix, 3.8.1 Inverse of Matrices by Elementary Operations (Retain Ques. 18 of Exercise 3.4), Page 98 Example 26, Page 100-101 Ques. 1–3 and 12 (Miscellaneous Exercise), Page 102 Third Last Point of Summary.
Matrices Important Formulae for CBSE and Competitive Exams
Students can check important formulae and basic concepts of the Matrices chapter below for a better understanding of questions. Students can also use these formulae to solve exercises.
Matrix Basics
- Order of a Matrix:
- If a matrix has rows and columns, its order is .
- Elements:
- , where represents the element in the row and column.
Matrix Operations
-
Addition/Subtraction:
-
Scalar Multiplication:
-
Matrix Multiplication:
- Condition: Number of columns in = Number of rows in .
-
Transpose of a Matrix:
Properties of Matrix Operations
-
Transpose Properties:
-
Symmetry:
-
Identity Matrix Properties:
Determinant and Inverse of Square Matrices
-
Adjoint Formula for Inverse:
-
Determinant Property:
Applications of Matrcies
- Solving Linear Equations:
- Consistency of Linear Equations:
- If , the system has a unique solution.
Class 12 Math Chapter 3 Matrices Solution PDF: Free Download
We have uploaded the complete exercise-wise solution of Matrices Class 12 NCERT PDF in one place. This Class 12 Chapter 3 Matrices NCERT Solution PDF is beneficial for all students in both CBSE boards and competitive exams; JEE Main, CUSAT CAT, BITSAT, etc... Students can access for free the Matrices Class 12 solutions pdf download below;
Class 12 Math Chapter 3 Matrices Solution: Free PDF Download
Class 12 Math Chapter 3 Matrices Exercise-wise Solutions
The class 12 Matrices Chapter focuses on several important topics, such as the Type of Matrices, zero, symmetric, and asymmetric Matrices, the Transpose and Inverse of Matrices, and other Matrices operations. Students will encounter different problems based on these concepts in the exercises. Each exercise deals with different concepts, Class 12 Matrices Exercise 3.1 deals with the basics of Matrix, its types and fundamentals. Class 12 Matrices Exercise 3.2 deals with operations of Matrix, its multiplication both scaler and vector and more advanced concepts. Class 12 Matrices Exercise 3.3 deals with problems finding the transpose and inverse of Matrix. Students can check Exercise-wise Class 12 Chapter 3 Matrices NCERT Solutions below;
Class 12 Math Chapter 3 Matrices Exercise 3.1 Solutions
Matrices exercise 3.1 solutions focuses on the basic concepts of matrices. Definition, types of Matrices, and basic operations of matrices are several topics discussed in the solutions of Matrices Class 12 Exercise 3.1. Chapter 3 Matrices Exercise 3.1 includes 10 Questions (7 Short Answers, 3 MCQs). Students can find the solution of exercise 3.1 below;
Matrices Exercise 3.1 Solutions
Q2. If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
A.2. As, number of elements of matrix having order m × n = m.n.
(b) So, (possible) order of matrix with 24 elements are (1 × 24), (2 × 12), (3 × 8), (4 × 6), (6 × 4), (8 × 3), (12 × 2), 24 × 1).
Similarly, possible order of matrix with 13 elements are (1 × 13) and (13 × 1)
Q3.If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
A.3. As number of elements of matrix with order m × n
(E) Possible order of matrix with 18 elements are (1 × 18), (2 × 9), (3 × 6), (6 × 3), (9 × 2) and (18 × 1)
Similarly, possible order of matrix with 5 elements are (1 × 5) and (5 × 1)
Q4.Construct a 2 × 2 matrix, , whose elements are given by:
(ii) (iii)
A.4. (E) (i) aij such that i = 1, 2 and j = 1 × 2 for 2 × 2 matrix
Therefore a11 = A 2×2 =
a12 =
a21
a22 =
Q5.Construct a 3 × 4 matrix, whose elements are given by:
(i) (ii)
A.5. (E) (i) aij = such that i = 1, 2, 3 and j = 1, 2, 3, 4 for 3 × 4 matrix
So, a11= .
a12 =
a14 =
a21 =
a22 =
a23 =
Q6. Find the values of x, y and z from the following equations:
A.6. (i)
corresponding
By equating the elements of the matrices, we get,
x= 1
y= 4
z= 3.
(ii)
By equating the corresponding elements of the matrices we get,
x+ y = 6 (I)
5 + Z = 5
xy = 8
x
putting eq in (1) we get
+ y = 6.
8 + y2 = 6y
y2 6y + 8 = 0.
y2 - 4y - 2y + 8 = 0
y (y-4) -2 (y-4) = 0
(y-4) (y-2) = 0
y= 4 0r y = 2.
When y = 4,x= 6-y = 6-4 = and z = 0.
Wheny = 2,x = 6-y = 6-2 = 4 and z = 0.
By equating the corresponding elements of the matrices we get,
x+ y + z = 9 -------(i)
x + z = 7 --------(ii)
y + z = 7 -------(iii)
Subtracting eqn (3) from (1) and (2) from (1) we get,
x + y + z -y - z = 9 - 7 and x + y + z - x - z = 9 - 5
x = 2 and y = 4 .
Putting x = 2 in eqn (2)
2 + z = 5
z = 5 - 2 = 3.
So, x = 2,y = 4, z = 3.
Q7. Find the value of a, b, c and d from the equation:
A.7.
(5) Equating the corresponding elements of the matrices we get,
a - b = -1 --------(i)
2a + c = 5 ------(2)
2a - b = 0 ----(3)
3c + d = 13 -----(4)
Subtracting eqn(1) from (3) we get,
2a - b (a - b) = 0-(-1)
2a - b - a+ b = 0 + 1 = 1
[a= 1]
Put we get,
2 × 1 + c = 5 c = 5 - 2 [c = 3]
Put (4) we get,
3 × 3 + d = 13 => d = 13 - 9 [d = 4.]
put we get, 1 - b = -1 b = 1 + 1 [b= 2]
Q8.A= is a square matrix, if
(A) m n (C) m = n (D) None of these
A.8. is a square matrix if m = n
(E) Option C is correct.
Q9.Which of the given values of x and y make the following pair of matrices equal:
(B) Not possible to find (C)
(D)
A.9. For the matrices to be equal, the corresponding elements
(B) heed to be equal so,
Fora11, 3x+ 7 = 0
3x = -7.
x =
fora12, 5 = y - 2
y = + 5 + 2 = 7.
For a21, y + 1 = 8
y = 8 - 1 = 7.
fora22, 2 - 3x = 4.
3x = 2 - 4
As the variable x and y has more than one value which is not peacetable.
Option B is correct.
Q10.The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(A) 27 (B) 18 (C) 81 (D) 512
A.10. A 3 × 3 order matrix will have 9 elements
(M) Since, the elements can be either 1 or number of choices for each element is 2 .
The required no. of arrangement = 29(4,2 × 2 × 2 9 times ) 512
So, option D is correct.
Class 12 Math Chapter 3 Matrices Exercise 3.2 Solutions
Class 12 Matrices Exercise 3.2 deals with problems based on the operations performed on matrices such as addition, subtraction, scalar multiplication, and their properties. The Matrices exercise 3.2 includes 22 Questions 14 Long, 6 Short, and 2 MCQs. Students can check the complete exercise 3.2 solution below;
Matrix Exercise 3.2 Solutions
Q1 Let
Find each of the following:
(i) A + B (ii) A – B (iii) 3A – C (iv) AB (v) BA
A.1. A B C
(i) A + B =
(ii) A - B =
(iii) 3A - C = 3
=
(iv) AB =
=
Q2.Compute the following:
(i) (ii)
(iii) (iv)
A.2. (I)
Q4.if and then compute
(A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
A.4 A + B =
Now
L.H.S. = a+ (b - c) =
R.H.S. = (a+ b) - c =
= L.H.S.
∴A + (B - C) = (A + B) - C
Q5.If and then compute 3A – 5B.
A.5. 3a - 5b = 3 × -
=
Q6.Simplify
A.6..
(E)
Q7.Find X and Y, if
(i) and
(ii) and
A.7. (i) x + y =
x - y =
(ii)2x + 3y = ___ (1)
2x + 2y = _____ (2)
Multiplying eqn by 2 and
2 × (2x+ 3y) = 2 ×
4x + 6y =
4x + 6y =
3 × (3x+ 2y) = 3 ×
9x + 6y =
Subtracting eqn (iii) from (iv) we get,
4x+ 6y - (4x+ 6y) =
5x =
From eqn (u);
y
Q8.Find X, if and
A.8. Give, 2x + 4 =
y
Q9.Find x and y, if
A.9. Given,
Equating the corresponding elements of the matrices we get,
2 + y = 5
y = 5 - 2 = 3
And 2x + 2 = 8
2x = 8 - 2
x = 3
∅x = 3, y - 3.
Q10.Solve the equation for x, y, z and t, if
A.10.
Equating the corresponding elements of the matrices get,
2x + 3 = 9
2x = 9 - 3
x = 3
2z - 3 = 15
2z = 15 + 3
z = 9
2y = 12
=> y = 6
2t + 6 = 18
2t = 18 - 6
2t = 12 => t = t = 6
3x + y = 5 _____ (ii)
Adding (i) and (i) we get,
2x - y + 3x + y = 10 + 5.
5x = 15
=> x = 3
5x = 15
=> x = 3
Putting x = 3 in (i) we gel,
2 × 3 - y = 10
6 - 10 = y
y = -4
Q12.Given , find the values of x, y, z and w.
A.12. Given,
Q13.If F , show that F(x) F(y) = F(x + y).
A.13. Given,
So, F(y)
Q14.Show that
(i)
(ii)
Q15.Find – 5A + 6I, if
A.15.. Given, A =
A2 = AA2 =
=
Q16 If prove that
A.16. Given A =
A2 = AA =
A3 = A2A =
So, A3-6A2 + 7A + 2I
(2000 matrix )
Hence proud
Q17.If and , find k so that A
A.17. Given,A =
A2 = A. A =
So,A2= xA2I.
Q19.A trust fund has 30,000 that must be invested in two different types of bonds.
The first bond pays 5% interest per year, and the second bond pays 7% interest
per year. Using matrix multiplication, determine how to divide 30,000 among
the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) 1800 (b) 2000
A.19. let x be the investment in the first bond out of total `30,000.
(M) then, investment use for the second bond = ` 30,000 - x.
Hence, investment matrix A =
As there is 5% and 7% interest paid the first and second , (per year)
Manual total interest = `
(a) Given, manual total interest = ` 1800.
` 210.000 - `180,000 = 2x
x = ` 15, 000
∴investment in first and second bond is x = 15,000 and ` 30,000 –x = ` 30,000 - `15,000 - ` 15,000 respectively.
(B) given ,Annual total interest = ` 2000.
` 2,10, 000 - ` 2,00,000
` 2,10, 000 - `2; 000 = 2x
x = ` 5,000
∴investment in first and second hand is x = 5,000 and. 30,000 - x = 30,000 - 5,000 = 25,000 respectively
Q20.The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are `80, `60 and`40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k, respectively. Choose the correct answer in Exercises 21 and 22.
= (9600 + 5760 + 4800)
= ` 20160
Order of matrices ,
Q21.The restriction on n, k and p so that PY + WY will be defined are:
(A) k = 3, p = n (B) k is arbitrary, p = 2 (C) p is arbitrary, k = 3 (D) k = 2, p = 3
A.21. For, PY + WY to be defined
(E) P should be seen that number of columns of p
Should, be equal to no of nous of yi.e,[x = 3]
n × 3 and (PY)(p × x)
similarity, in W n×3Y 3×xwe see thatno of columns of
W = no of rows in Y and (WY) n × x.
Again,PY + WY is defined if order of (PY) p × k and (WY)n × u are the sameie ,P = n
so, option a is correct .
Q22.If n = p, then the order of the matrix 7X – 5Z is:
(A) p × 2 (B) 2 × n (C) n × 3 (D) p × n
A.22. The order of 7x - 5z will be same as order of x and z
as has order 2 × n and z has order 2 × p.and given n = p.
7x - 5z has order 2 × n
∴option b is correct.
Class 12 Math Chapter 3 Matrices Exercise 3.3 Solutions
Class 12 Chapter 3 Matrices Exercise 3.3 delves into the multiplication of matrices, Which is the key concept of Matrix. Exercise 3.3 deals with Matrix Multiplication; Scalar & Vector, Conditions for Multiplication, Properties of Matrix Multiplication, and other applications of Matrix multiplication. Matrices Exercise 3.3 Solutions includes 12 Questions (10 Short Answers, 2 MCQs) in total, Students can check complete solution of the exercise;
Matrices Exercise 3.3 Solutions
Q1.Find the transpose of each of the following matrices:
(i)
(ii)
A.1. (i) Let A=
Then, A’ = [5 ½ − 1] 1 × 3
(ii) Let A =
Then, A’ =
(iii) Let A =
Then A’ =
Q2.If
(i) (A + B)'= A'+ B', (ii) (A – B) '= A'– B'
A.2. Given, A =
Then, A’ =
A + B =
LHS. = (A + B)’ =
RHS = A’+ B’ =
(ii) A – B =
L.H.S. = (A − B)’ =
R.H.S. = A’ − B’ =
Q6.If (i)
(ii) If
A.6. (i) Given, A =
Then, A’ =
∴A’ A =
=
=
=
= A ’ A = 1.
Given,
(ii) 1 A =
Then, A’ =
∴A’ A =
=
=
=
Q7.(i) Show that the matrix
(ii) Show that the matrix
A.7. (i) Given A =
Then, A’ =
∴A’ = A.
Here, A is symmetric matrix
Given, A =
Then, A’ =
Hers A is a show symmetric matrix.
Q8.For the matrix
(i) (A + A') is a symmetric matrix
(ii) (A – A') is a skew symmetric matrix
A.8. Given, A =
Then, A’ =
Let P = A + A’ =
So, P’ =
i e, ( A + A’ )’ = A + A’.
Hence, A + A’ is symmetric matrix.
Let Q = A A’ =
So,Q1 =
i e, (A A’)’ = -(A - A’).
Have, A - A’ is a show symmetric matrix
Q9.Find
A.9. Given, A =
Then, A’ =
So, A + A’ =
And A - A’ =
=
Q10. Express the following matrices as the sum of a symmetric and a skew symmetric
matrix:
(i)
(iii)
Choose the correct answer in the Exercises 11 and 12.
A.10. (i) Let A =
Then, A’ =
Let P =
=
Then, P’ =
∴ P =
Let Q =
=
Then Q.’ =
∴ Q =
Now, P + Q =
This A is represented as a sun of symmetric and skew symmetric matrix
Let A =
Then A’ =
Now, A + A’ =
=
Let P =
Then, P’ =
∴ P =
A - A’ =
Let Q =
Q’ = (-1)
∴ Q =
Have P + Q =
Then A is represented as a sum of symmetric & skew symmetric matrix
(iii) Let A =
Then, A’ =
Let P =
=
=
Then P’ =
∴ P =
Let Q =
=
=
Then Q’ =
∴ Q =
∴ P + Q = symmetric
= ..
=
Thus A is represented as a sum of symmetric and skew symmetric matrix.
Let A =
Then A’ =
Let P =
=
Then, P’ =
∴ P =
=
Thus, Q’ =
∴ Q =
∴ P + Q =
=
Thus A is represented as a sum of symmetric and skew symmetric matrix
Q11.If A, B are symmetric matrices of same order, then AB – BA is a
(A) Skew symmetric matrix (B) Symmetric matrix
(C) Zero matrix (D) Identity matrix
A.11. Given A and B are symmetric matrices,
(E) Then, A’ = A and B’ = B.
Now, (AB - BA)’ = (AB)’- (BA)’
= B’A’ - A’B’.
= BA - AB
(AB - BA)’ = -(AB - BA)
AB - BA is a skew symmetric matrix
∴ Option A is correct.
Q12.If
A.12. Given, A =
and A + A’ = I.
Equating the corresponding element of the matrix we get,
2 cos
Option B is correct
Class 12 Math Chapter 3 Matrices Exercise 3.4 Solutions
Class 12 Chapter 3 Exercise 3.4 involves the transpose of a matrix, the properties of transpose, and the concepts of symmetric and skew-symmetric matrices. these topics and this exercise are very important for CBSE board exams. Matrices exercise 3.4 Solutions includes 18 Questions (4 Long, 13 Short, 1 MCQ). Students can check the complete solution of exercise 3.4 below;
Matrices Exercise 3.4 solutions
Q1.
A.1. Let A=
We write A = IA.
∴ A-1 =
Q2.
A.2. Let A =
We write, A = IA.
∴ A-1 =
Q3.
A.3. Let A =
We write, A = IA.
∴A-1 =
Q4.
A.4. Let A =
We write, A = 1A.
∴ A-1 =
Q5.
A.5. Let A =
We write, A = IA,
∴A-1 =
Q6.
A.6. Let A =
We write, A = IA
∴ A-1 =
Q7.
A.7. Let A =
We write A = IA.
∴ A-1 =
Q8.
A.8. Let A =
We write A = IA
∴ A-1 =
Q9.
A.9. Let A =
We write, A = IA.
∴ A-1 =
Q10.
A.10. Let A =
We write A = IA.
∴ A-1 =
Q11.
A.11. Let A =
We write, A = IA.
∴A-1 =
Q12.
A.12. Let A =
We write A = IA.
As all the elements of 2nd row on the lift side matrix are 2000, A-1 does not exit .
Q13.
A.13. Let A =
We write A = IA.
∴A-1 =
Q14.
A.14. Let A =
We write, A = IA.
∴A-1 does not exit
Q15.
A.15. Let A =
We write, A = IA
∴A-1 =
Q16.
A.16. Let A =
We write A = IA
∴A-1 =
Q17.
A.17. Let A =
∴ A1 =
Q18.Matrices A and B will be inverse of each other only if
(A) AB = BA (B) AB = BA = 0
(C) AB = 0, BA = I (D) AB = BA = I
A.18. Matrices A and B will be inverse of each other if.
(E) AB = BA = I.
Here option D is correct.
Class 12 Math Chapter 3 Matrices Miscellaneous Exercise Solutions
Class 12 Math important reference books and preparation Tips
Maths Ncert Solutions class 12th Exam
Student Forum
Answered 22 hours ago
Class 12 Math Relation and Function chapter have moderate weightage in the JEE Mains exam. Relation and function combined with sets comprises of 4-8 marks weight in the JEE Mains Exam. However, Students should know there is no fixed weightge of relation and fucntions chapter. Questions may be asked
E
Beginner-Level 2
Answered 22 hours ago
Candidates must be aware of the important concepts discussed in the chapter and their application in other mathematics chapters. Students can check several fundamental and advanced topics discussed in the Relation and Function chapter.
- Basic Concepts: Definations, Sets cross product, Relation, Functi
P
Beginner-Level 2
Answered 23 hours ago
Yes, Class 12 Math Relation and Function chapter is important for rither CBSE Board Exams or State Boards. The Relation and Function chapter have weightage of 6-8 marks in the CBSE board exam. Moreover Relation and function chapter forms the foundation for many other advanced topicssuch as types of
A
Beginner-Level 2


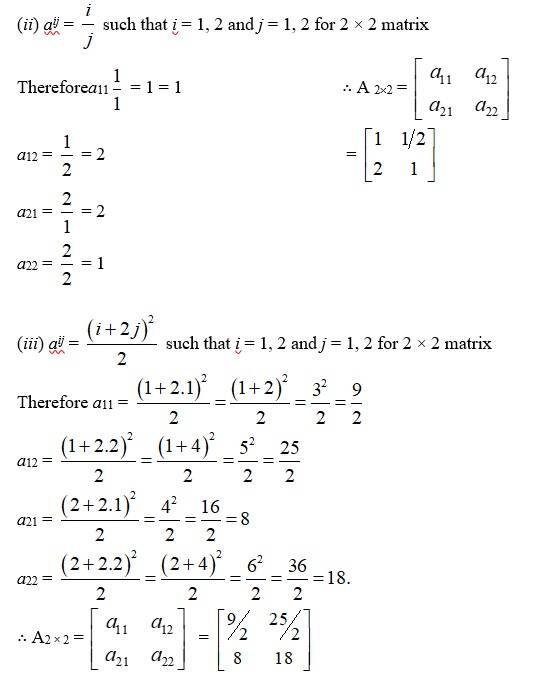

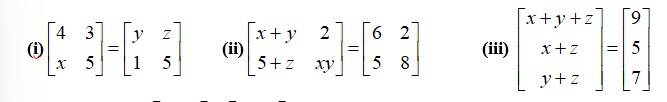
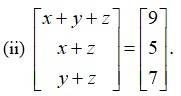
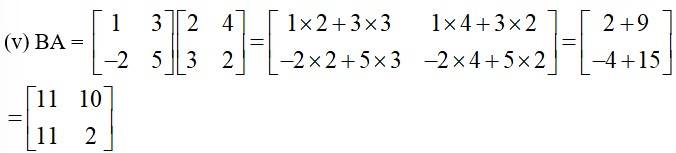
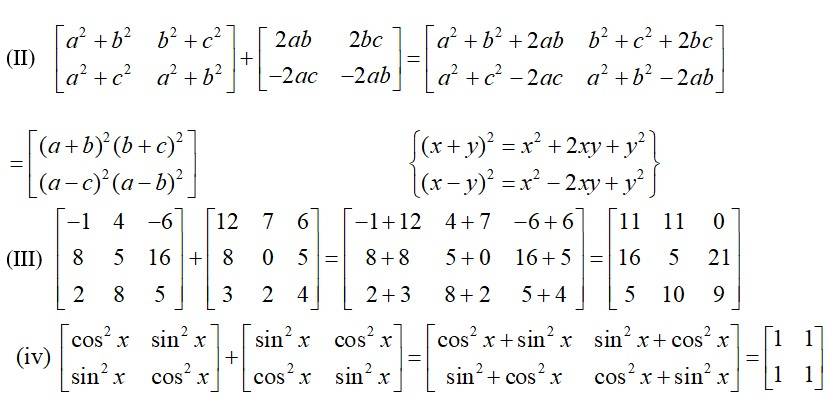




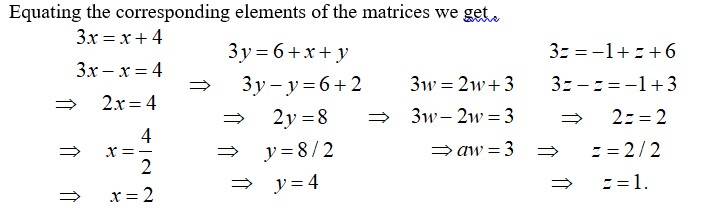
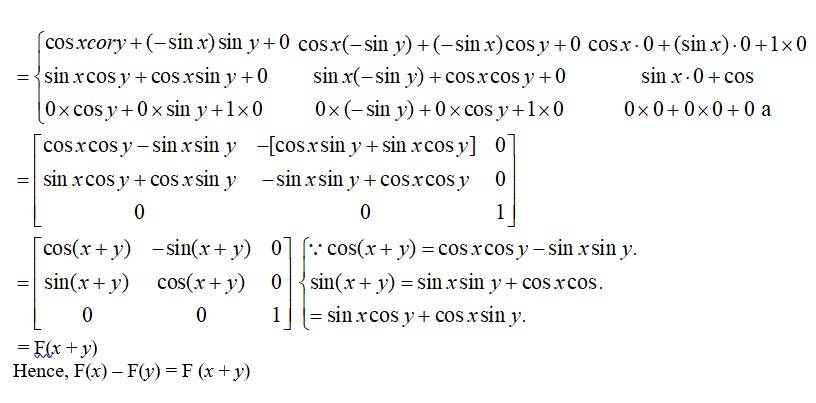

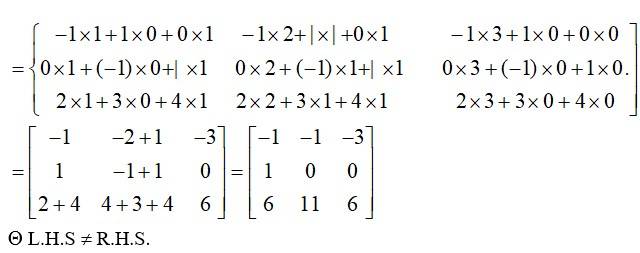

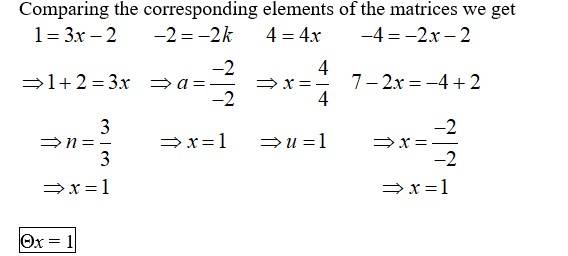



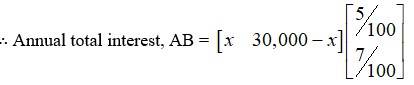






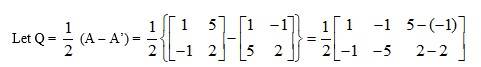

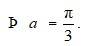








What is weightage of Relation and Function in JEE Main?