
Class 12 Chapter 10 Vector Algebra NCERT Solutions: Students can access complete NCERT solutions for Class 12 Chapter 10 Vector Algebra provided by Shiksha. This chapter is immensely important for competitive exam aspirants due to high weightage. Class 12 Math Vector Algebra delves into topics such as types of vectors; Position vectors, Direction cosines, Zero Vectors, Unit Vector, Coinitial Vectors, Collinear Vectors, Equal Vectors, Negative Vector, addition of vectors etc. Class 12 Math Chapter 10 Vector Algebra focuses on the usage of vectors for calculating quantities which include magnitude and direction, and the concepts of vector algebra are very important to solve many numerical problems in Physics.
Class 12 Math Vector Algebra NCERT Solutions will be very useful for both board and entrance exam students and its concepts are used in Physics problems also. We have prepared complete Vector Algebra NCERT Solutions of NCERT Textbook by our experts to help students. Students can download the complete Exercise-wise NCERT Class 12 chapter 10 Vector Algebra solution PDF through the below link on this page.
Students can use the Vector Algebra Class 12 Math Solution PDF to strengthen their concepts for CBSE Boards as well as other Entrance exams such as JEE Main, CUSAT CAT, etc. Students should also check the Class 12 Chapter 11 Three-dimensional Geometry NCERT solutions, which can help to get a better understanding of Vector Algebra.
Class 12 Math Vector Algebra explores many key topics such as vector quantities, vector addition, resultant, orthogonal triad, cross product, dot product and area of 2D and 3D planes.Students can access the complete Class 11 Math chapter-wise Solutions and Class 12 Chapter-wise Math solutions on Shiksha. For more information check below;
| Other Important Math Chapter Solutions | ||
|---|---|---|
| Class 12 Chapter 6 Application of Derivatives Solutions | Class 11 Chapter 8 Application of Integrals Solutions | Class 12 Chapter 9 Differential Equations Solutions |
- Class 12 Math Chapter 10 Vector Algebra : Key Topics, Weightage & Important Formulae
- Class 12 Math Chapter 10 Vector Algebra NCERT Solution PDF: Free PDF Download
- Class 12 Vector Algebra Exercise-wise NCERT Solutions
- Class 12 Vector Algebra Exercise 10.1 Solutions
- Class 12 Vector Algebra Exercise 10.2 Solutions
- Class 12 Vector Algebra Exercise 10.3 Solutions
- Class 12 Vector Algebra Exercise 10.4 Solutions
- Class 12 Vector Algebra Miscellaneous Exercise Solutions
- Class 12 Math Preparation Tips and Recommended Books
Class 12 Math Chapter 10 Vector Algebra : Key Topics, Weightage & Important Formulae
Class 12 Math Chapter 10 Vector Algebra carries around 6–8 marks in the CBSE board exams and almost the same in the state board exams. As per notification, Vector Algebra is combined with 3D Geometry in the JEE Main syllabus, these two chapters carry a weightage of approximately 10–12% of the mathematics section. Vector Algebra and Three-Dimensional Theory include very important topics vector addition, vector multiplication; cross, and dot product, and many more. Students can check the key topics and important formulae below;
Class 12 Vector Algebra Key Topics
- Basics of Vectors: Representation of vectors in 2D, 3D.
- Types of Vectors: Unit, Position, Co-initial, collinear, and coplanar vectors
- Operations: Addition, subtraction, and multiplication by a scalar
- Properties of vector addition and scalar multiplication and Scalar Product of Vectors
- Applications: Angle between two vectors, projection of one vector onto another
- Properties of cross-product: Geometric interpretation, Area of a parallelogram, Triangle,
- Applications: Conditions for coplanarity of three vectors, Vector Equations of lines, and planes
Check out for Class 12 Vector Algebra Dropped Topics – 10.7 Scalar Triple Product, 10.7.1 Coplanarity of Three Vectors.
Class 12 Math Chapter 10 Vector Algebra Important Formulae for CBSE and Competitive Exams
Students can check the important topics below;
Basic Vector Operations
- Position Vector: A point in 3D space has a position vector:
- Addition of Two Vectors: If and then:
- Magnitude of a Vector: For a vector
- Dot Product (Scalar Product): If and , then;
- Angle between Two Vectors:
- Cross Product (Vector Product): If and , then;
- Magnitude of Cross Product:
- Projection of a Vector:
-
Projection of on :
-
Vector Component of along :
- Collinearity of Two Vectors: Two vectors and are collinear if;
- Vector Equation of a Line
-
Vector form: A line passing through and parallel to :
-
Cartesian form: A line passing through and parallel to :
Class 12 Math Chapter 10 Vector Algebra NCERT Solution PDF: Free PDF Download
Shiksha has compiled the complete exercise-wise solution of the Class 12 Vector Algebra NCERT PDF in one place prepared by our experts. Students can use Class 12 Vector Algebra Solutions to build a strong conceptual understanding of Vector and 3D geometry. The Vector Algebra Class 12 NCERT Solution PDF will be useful for both CBSE boards and competitive exams aspirants; JEE Main, CUSAT CAT, BITSAT, etc... Students can access the Vector Algebra Class 12 Solutions pdf download for free below;
Class 12 Math Chapter 10 Vector Solution PDF: Free PDF Download
Class 12 Vector Algebra Exercise-wise NCERT Solutions
This chapter introduces concepts like vector operations, dot and cross products, scalar triple products, and their real-world significance. Mastering these topics is crucial for excelling in board exams and competitive entrance tests.
Class 12 Vector Algebra Exercise 10.1 Solutions
Class 12 Vector Algebra Exercise 10.1 Solutions
Class 12 Vector Algebra Exercise 10.1 deals with key concepts such as vectors, their representation, operations like addition, subtraction, and scalar multiplication, as well as their geometric interpretations. Shiksha has provided detailed solutions to all the problems in Vector Algebra Exercise 10.1, ensuring that students grasp the concepts thoroughly. Vector Algebra Class 12 Exercise 10.1 Solutions consists of 5 Questions. Students can check the complete solution for VEctor Algebra Exercise 10.1 below;
Class 12 Vector Algebra Exercise 10.1 Solutions
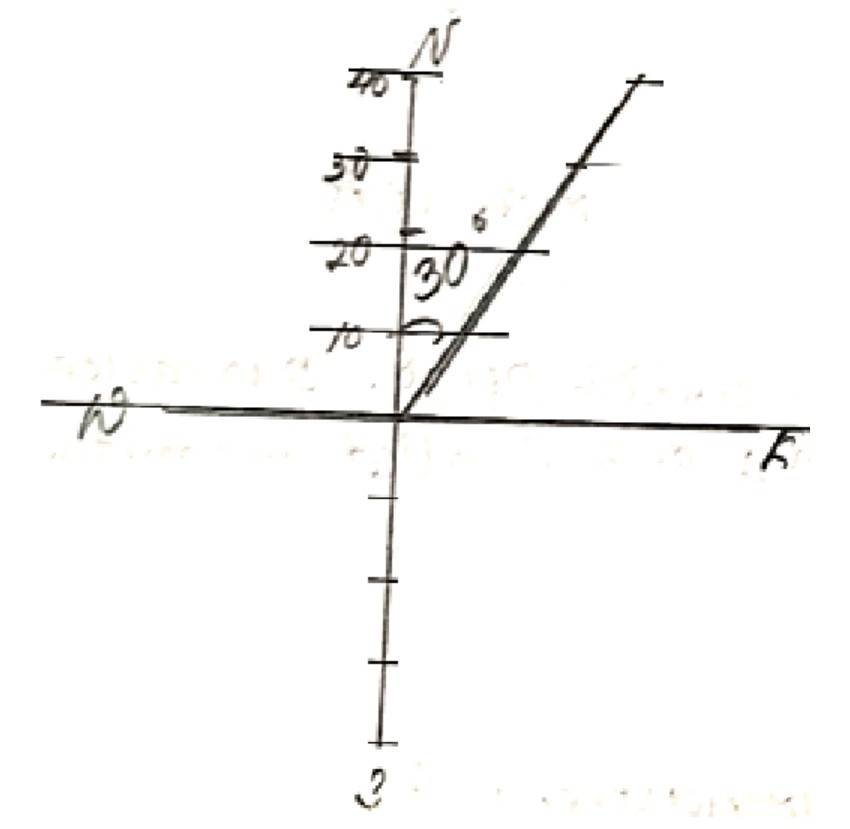
Q1. Represent graphically a displacement of 40 km, 30° east of north.
A.1. east of north.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 Watt
(v) 10–19 coulomb
(vi) 20 m/sec2
A.2. (i) 10kg involves only magnitude. So, it is scalar quantity.
(ii) 2 meters north-west involves both magnitude and direction. So, it is vector quantity.
(iii) 400 involves only magnitude. So, it is scalar quantity.
(iv) 400 watts involves only magnitude. So, it is scalar quantity.
(v) 10-19 coulomb involves only magnitude. So, it is scalar quantity.
(vi) 20m/s-2 involves magnitude and direction. So, it is vector quantity.
Q3. Classify the following as scalar and vector quantities:
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
A.3. (i) Time period involves only magnitude. So, it is scalar quantity.
(ii) Distance involves only magnitude. So, it is scalar quantity.
(iii) Force involves both magnitude and direction. So, it is vector quantity.
(iv) Velocity involves both magnitude and direction. So, it is vector quantity.
(v) Work done involves only magnitude. So, it is scalar quantity.
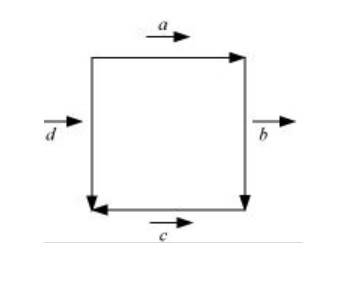
Q..4. In the adjoining figure, (a square) identify the following vectors:
(ii) Equal
(iii) Collinear but not equal.
A.4.
(a) Vector and are co initial same initial point.
(b) and same magnitude & direction.
(c) and are collinear but not equal they are parallels their direction are not same.
Q5. Answer the following as true or false:
(i) and - are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
A.5. (i) True, as vector quantity and - are parallel to same line.
(ii) False, as collinear vector are those vectors that are parallel to same line, but it is
not necessary that they are equal also.
(iii) False, as two vectors having same magnitude may have different directions, so
they are not collinear.
(iv) False, as two collinear vectors having same magnitude are not equal whey they
are opposite in direction.
Class 12 Vector Algebra Exercise 10.2 Solutions
Class 12 Chapter 10 Vector Algebra Exercise 10.2 focuses on advanced concepts such as the dot product (scalar product) and its applications in finding angles between vectors, the projection of one vector on another, and more. These concepts are not only crucial for board exams but also form the foundation for higher studies in physics, engineering, and applied mathematics. Vector Algebra Exercise 10.2 Solutions consist of 19 Questions. Students can check the complete Vector Algebra Exercise 10.2 solutions below
Class 12 Vector Algebra Exercise 10.2 Solutions
Q1 Compute the magnitude of the following vectors:
Q2. Write two different vectors having same magnitude.
A.2. Two different vectors having same magnitude: -
(i)
(ii)
Q3. Write two different vectors having same direction.
A.3. Two different vectors having same directions: -
(i)
(ii)
Q4. Find the values of x and y so that the vectors are equal.
A.4. Note that two vector are equal only if their corresponding components are equal.
Thus, the given vectors and will be equal if and only if
Q5. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
A.5. Let the vector with initial point P (2,1) and terminal point Q. (-5,7) can be
shown as,
The scalar components are -7 and 6.
The vector components are -7i and 6j.
Q6. Find the sum of the vectors:
A.6. The given vectors are
The sum of the vector is
Q7. Find the unit vector in the direction of the vector
Q8. Find the unit vector in the direction of the vector where P and Q. are the points (1, 2, 3) and (4, 5, 6) respectively.
A.8. Given,
So,
Q9. For given vectors , find the unit vector in the direction of
A9. Given,
The sum of given vectors is given by
Q11. Show that the vectors are collinear.
A.11. Let,
It is seen that
Where,
Therefore, we can say that the given vector are collinear.
Q12. Find the direction cosines of the vector
A.12. Let
Q13. Find the direction cosines of the vector joining the points A (1, 2, –3) and B (–1, –2, 1) directed from A to B.
A.13. Given, A(1,2,-3) and (-1,-2,1)
Now,
Then,
Let, l, m, n be direction cosine,
Therefore, direction cosine of are
Q14. Show that the vector is equally inclined to the axes OX, OY and OZ.
A.14. Here,
Let,
Then,
Q15. Find the position vector of a point R which divides the line joining two points P and Q. whose position vectors are and - respectively, in the ratio 2 : 1
(i) internally
(ii) externally.
A.15. (i) The position vector of point R dividing the join of P and Q. internally in
the ratio 2:1 is,
(ii) The position vector of the point k dividing the join of P and Q. externally in the ratio 2:1
A15. (ii)
Q16. Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q. (4, 1, – 2).
A.16. The Position vector of mid-point R of the vector joining point P (2,3,4) and Q (4,1,-2) is given by;
Q17. Show that the points A, B and C with position vectors respectively form the vertices of a right angled triangle.
A.17. We have,
Now,
Hence,
Hence, given points from the vertices of a right angled triangle.
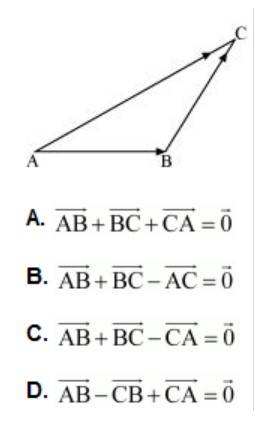
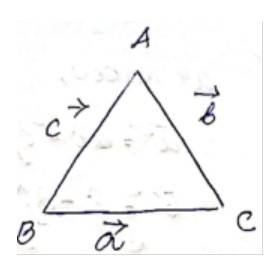
Q18. In triangle ABC (Fig. below), which of the following is not true:
A18. (A)
By triangle law of addition in given triangle, we get:
So, (A) is true.
(B)
So, (B) is true.
(C)
The eQ.uation in alternative C , which is not true, is incorrect.
(D)
The, equation given is alternative is D is true.
The correct answer is C.
Q.19. If and are two collinear vectors, then which of the following are incorrect:
(A) = λ for some scalar λ
(B) = ±
(C) The respective components of and are proportional.
(D) Both the vectors and have same direction, but different magnitudes.
A.19. We know,
If and are two collinear vector, they are parallel.
So,
Hence, the respective component are proportional but, vector and can have different direction.
Thus, the statement given in D is incorrect.
The correct answer is D.
Class 12 Vector Algebra Exercise 10.3 Solutions
Class 12 Chapter 10 Vector Algebra Exercise 10.3 focuses on the geometric interpretation of the cross product of vectors, its role in determining the area of parallelograms and triangles, and its significance in three-dimensional space. These concepts help, students in understanding the true nature of vectors and 3D planes. Vector Algebra Exercise 10.3 Solutions involves the solution of 18 Questions. Students can check the complete exercise 10.3 solutions below;
Class 12 Vector Algebra Exercise 10.3 NCERT Solutions
Q1. Find the angle between two vectors and with magnitude √3 and 2 respectively having . = √6
A.1. Given,
We have,
Now,
Also, we know,
on the vector
A.3. Let,
The projection of vector on is given by,
The projection of vector on is 0.
Q4. Find the projection of the vector on the vector
A.4. Let,
The project of vector on is.
Here, each of the given three vector is a unit vector.
Therefore, the given three vectors are mutually perpendicular to each other.
Q6. Find and ,if and
A.6. and ,if and
Q7. Evaluate the product
A.7.
Q8. Find the magnitude of two vectors and having the same magnitude such that the angle between them is 60° and their scalar product is 1/2.
A.8. Let be the angle between the vectors and .
It is given that
We know,
Magnitude of two vector=1
Q9. Find if for a unit vector .
A.9.
Q10. If are such that is perpendicular to then find the value of λ
A.10. Given,
Now,
If is perpendicular to , then
Therefore, the required value of is 8.
Q11. Show that is perpendicular to for any two non-zero vectors and
A.11.
Therefore, and are perpendicular.
Q12. If and . = 0 and . = 0 , then what can be concluded about the vector ?
A.12. We know,
and
Now,
is a zero vector.
Thus, vector satisfying can be any vector.
Q13. If and are unit vectors such that = 0 find the value of
A.13.
Q14. If either vector . But the converse need not be true. Justify your answer with an example.
A14. Consider
and
Then,
Q15. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors and ]
A.15. Vertices of are given as
is the angle between the vectors and
Q16. Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
A.16. Given, point are
Q17. Show that the vectors form the vertices of a right angled triangle.
A.17. Let vector and be position vector of point A, B, C respectively.
So,
Now, vectors and represents the sides of .
Hence,
Q18. If is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ is unit vector if
(A) λ = 1
(B) λ = –1
(C) a = | λ
|(D) a = 1/|λ|
A.18. Vector is a unit vector if
Now,
Therefore, vectar is a unit vector if a= .
Option (D)is correct.
Class 12 Vector Algebra Exercise 10.4 Solutions
Class 12 Vector Algebra Exercise 10.4 focuses on the scalar triple product and its applications. This exercise especially deals with computing the scalar triple product, its geometric interpretation in determining the volume of parallelepipeds, and its properties. Vector Algebra Class Exercise 10.4 Solutions comprises 12 Questions. Students can check the complete Vector Algebra Exercise 10.4 solution below;
Class 12 Vector Algebra Exercise 10.4 Solutions
Q.1. Find if and
Q2. Find a unit vector perpendicular to each of the vectors
A.2. Given,
A vector which is perpendicular to both and is given by
Say
Therefore, the unit vector is
Q3. If a unit vector makes an angle π/3 with and an acute angle θ with then find θ and hence, the components of .
A3. Let as component
We know,
is a unit vector,
Given that,
marks angles with , with and with acute angle.
Now,
We know,
Q.4. Show that
A4. Show that
Q.5. Find λ and μ if
A5.
On comparing both side components,
Therefore, the value of and .
Q6. Given that and What can you conclude about the vectors and ?
A.6. Given,
and
For,
, then either or or
For,
, then either or or
In case and are non- zero on both side.
But and cannot be both perpendicular and parallel simultaneously.
So, we can conclude that
or
Q7. Let the vectors be given as then show that
A.7. Given,
Adding (2) and (3), we get
From (1) and (4), we have
Hence, proved.
Q8. If either = 0 and = 0 then Is the converse true? Justify your answer with an example.
A.8. We take any parallel non- zero vectors so that .
Q9. Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).
A.9. Given,
We have,
The area of given triangle is
A.10. Given,
The area of a parallelogram with and as its adjacent sides is given by
Q11. Let the vectors and such that | | = 3 and | | = √2/3 then is a unit vector, if the angle between and is:
(A)
(B)
(C)
(D)
A.11. (B) Given,
Hence, is a unit vector if angle between and is
Q12. Area of a rectangle having vertices A, B, C and D with position vectors respectively is:
(A)
(B) 1
(C) 2
(D) 4
A.12. (C)
Given,
Class 12 Vector Algebra Miscellaneous Exercise Solutions
Class 12 Math Preparation Tips and Recommended Books
Maths Ncert Solutions class 12th Exam
Student Forum
Answered 22 hours ago
Class 12 Math Relation and Function chapter have moderate weightage in the JEE Mains exam. Relation and function combined with sets comprises of 4-8 marks weight in the JEE Mains Exam. However, Students should know there is no fixed weightge of relation and fucntions chapter. Questions may be asked
E
Beginner-Level 2
Answered 22 hours ago
Candidates must be aware of the important concepts discussed in the chapter and their application in other mathematics chapters. Students can check several fundamental and advanced topics discussed in the Relation and Function chapter.
- Basic Concepts: Definations, Sets cross product, Relation, Functi
P
Beginner-Level 2
Answered 23 hours ago
Yes, Class 12 Math Relation and Function chapter is important for rither CBSE Board Exams or State Boards. The Relation and Function chapter have weightage of 6-8 marks in the CBSE board exam. Moreover Relation and function chapter forms the foundation for many other advanced topicssuch as types of
A
Beginner-Level 2


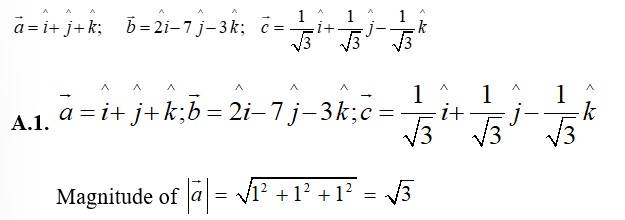
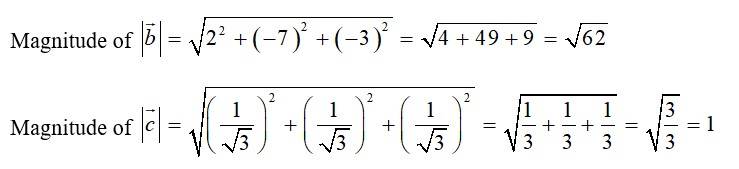
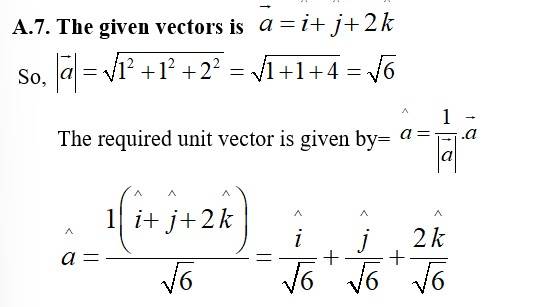
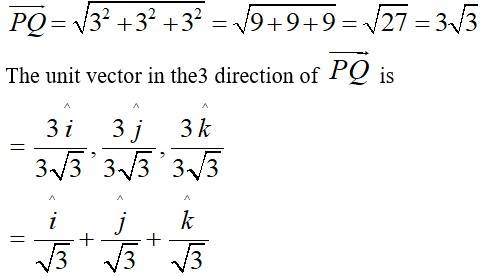



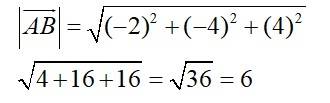
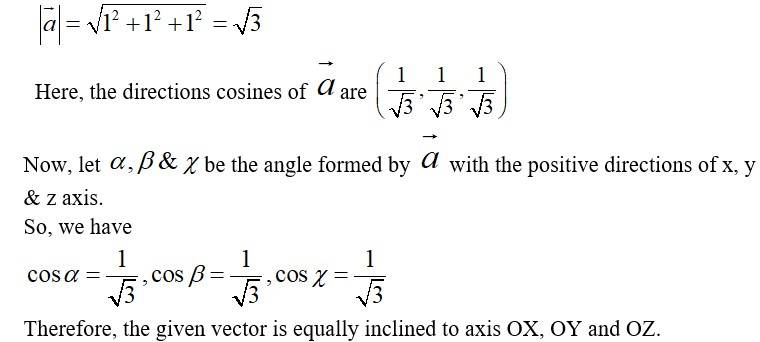
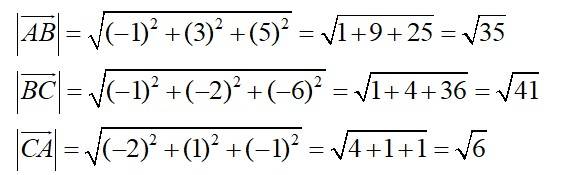


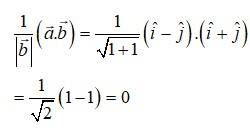

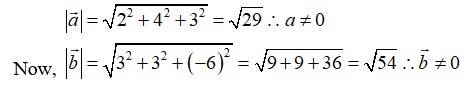
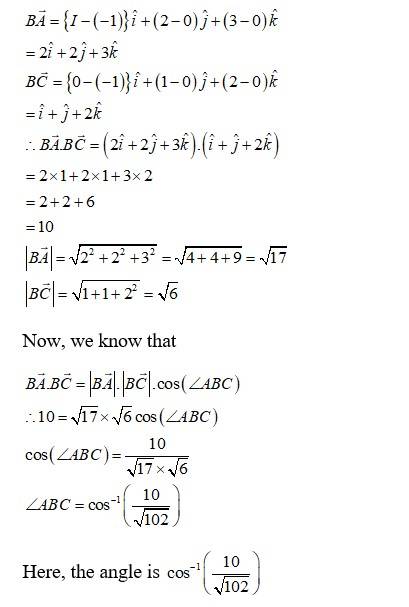
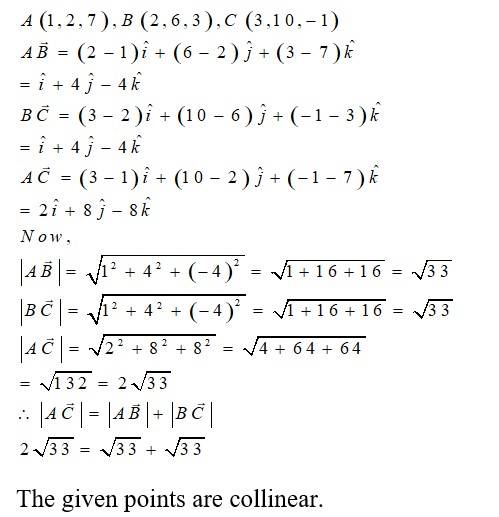
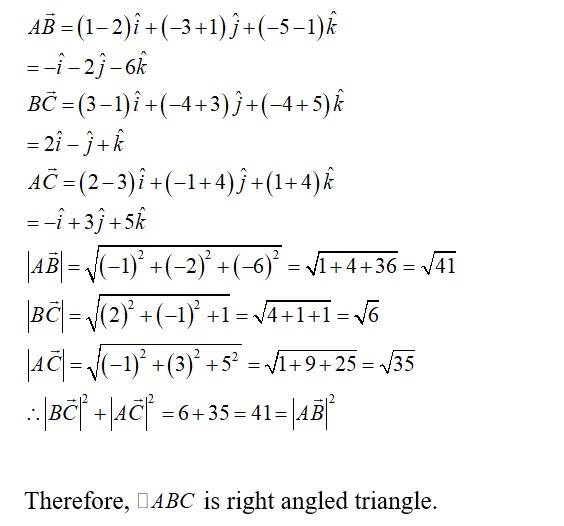
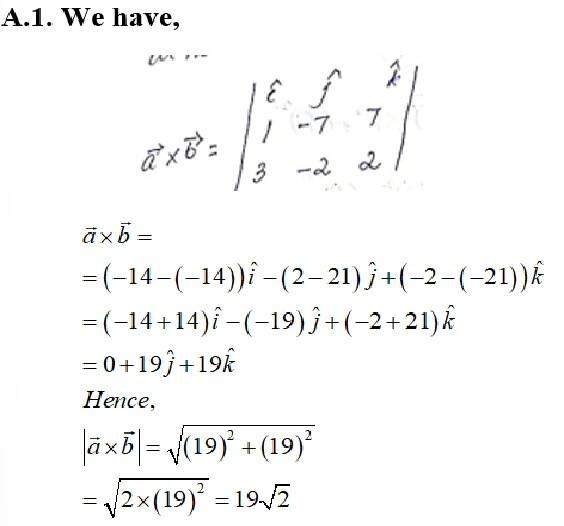


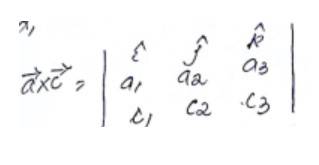



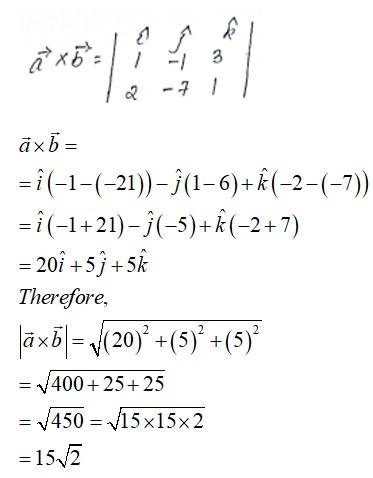

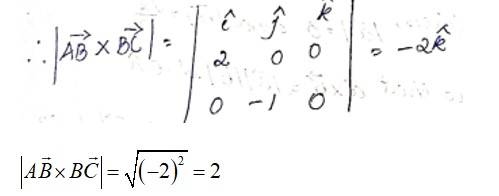


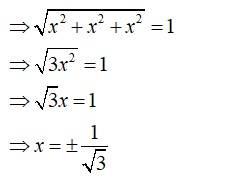


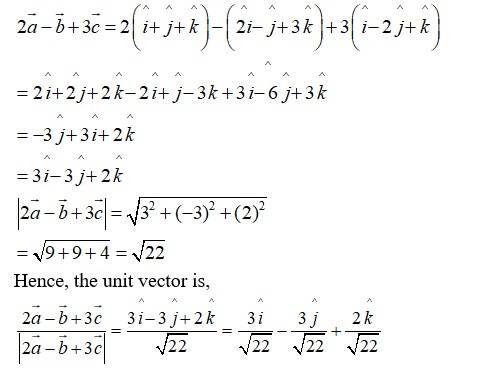


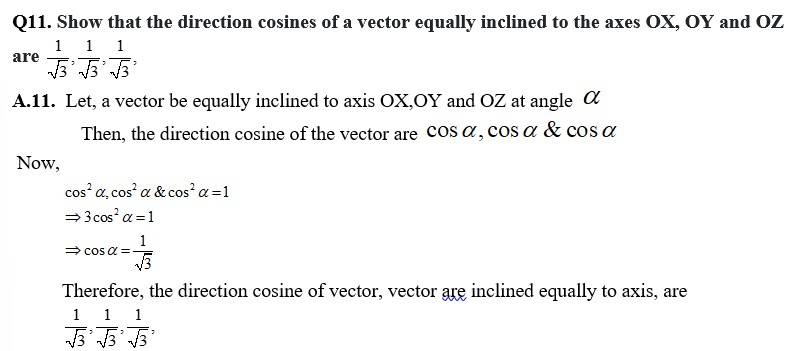
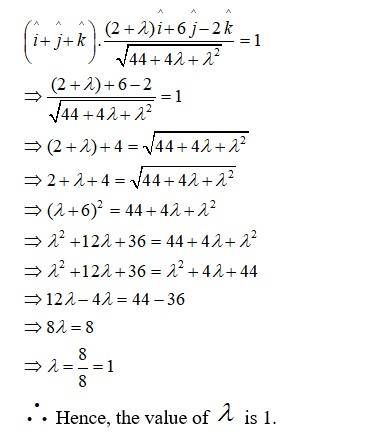
What is weightage of Relation and Function in JEE Main?