NCERT Solutions for Class 11 Physics Chapter 3 Motion in a Straight Line: Topic-wise Questions & Answers PDF

•       Introduction to Motion in Straight Line
•       Position, path length and displacement
•       Average velocity and average speed
•       Instantaneous velocity and speed
•       Acceleration
•       Kinematic equations for uniformly accelerated motion
•       Relative velocity

NCERT Class 11 Physics Motion in a straight line PDF explains the concepts of motion, path length, displacement, average velocity, instantaneous velocity, acceleration etc which helps the students in solving related problems confidently. The students can download the chapter PDF for future reference by clicking on NCERT Class 11 Physics Chapter 2 exercise Solutions PDF Download

Download Here: NCERT Solutions for Class XI Physics Motion in a Straight Line PDF

Q.3.1 In which of the following examples of motion, can the body be considered approximately a point object:

(a) a railway carriage moving without jerks between two stations.

(b) a monkey sitting on top of a man cycling smoothly on a circular track.

(c) a spinning cricket ball that turns sharply on hitting the ground.

(d) a tumbling beaker that has slipped off the edge of a table.

Ans.3.1 The length of the carriage is very small compared to the distance between 2 stations. Hence the carriage can be considered a point object.

The size of the monkey is very small compared to the length of the track, hence it can be considered as a point object.

The size of the cricket ball is comparable considering the distance between wickets, hence it cannot be considered as a point object.

The height of the beaker is comparable considering the height, from which it has fallen. Hence it cannot be considered as point object.

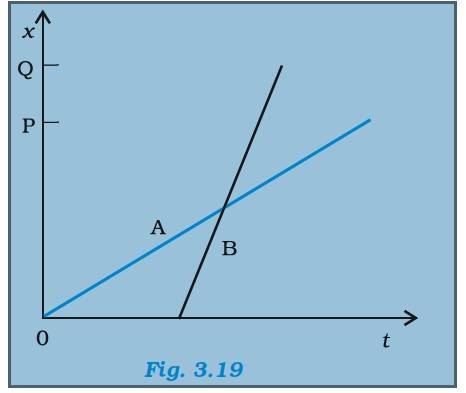
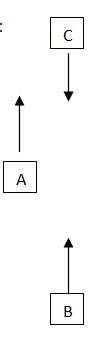
Q.3.2 The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. 3.19. Choose the correct entries in the brackets below;

(a) (A/B) lives closer to the school than (B/A)

(b) (A/B) starts from the school earlier than (B/A)

(c) (A/B) walks faster than (B/A)

(d) A and B reach home at the (same/different) time

(e) (A/B) overtakes (B/A) on the road (once/twice).

 

Ans.3.2  A lives closer to the school than B ( OP

A starts earlier than B from school. From the graph, A starts from O at time 0 whereas B starts after some finite value t.

B walks faster than as the slope for B is steeper than A.

Both B and A reaches home at the same time

At the intersection of the two lines, it is evident that B overtakes A once.

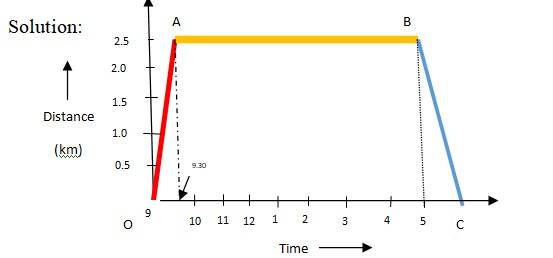
Q 3.3 A woman starts from her home at 9.00 am, walks with a speed of 5 km h^–1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h^–1. Choose suitable scales and plot the xt graph of her motion.

Ans.3.3 Office distance = 2.5 km

Walking speed = 5 kph

Time taken to reach office = 5/2.5 = 0.5 h

OA is the path to reach office

AB is the duration of office stay

Auto speed = 25 kph

Time taken by auto = 2.5/25 h = 6 minutes

BC is the path for returning

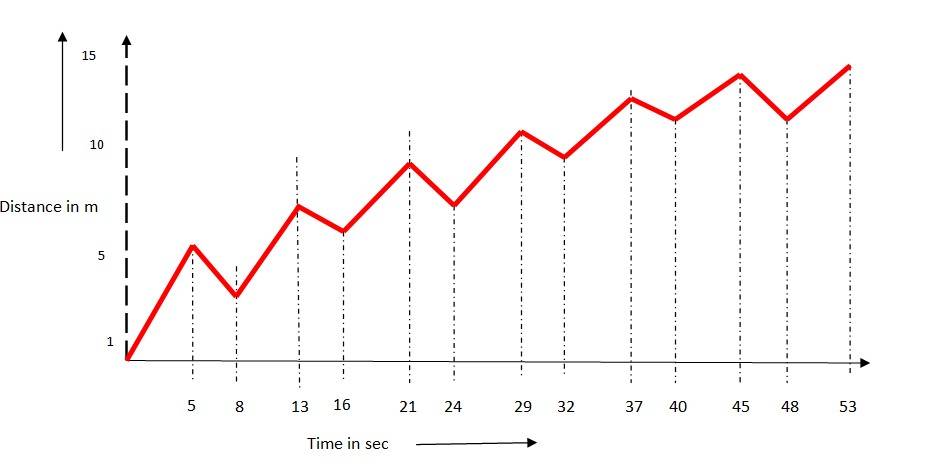
Q.3.4 A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1 s. Plot the xt graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.

Ans.3.4

The time taken for each step is 1s, he covers 5 m in 5 secs and goes backward by 3 m in 3 secs.

So in 8 s he covers 2 m. To cover 13m distance he needs to complete 8 m (13-5). To cover 8m, he will require 8 × 4 = 32 s. To fall in a pit, he needs to move anther 5m in 5s.

So total time taken = 32 +5 = 37 s

Q 3.5 A jet airplane travelling at the speed of 500 km h^–1 ejects its products of combustion at the speed of 1500 km h^–1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?

Ans.3.5 The speed of the jet plane, Vj = 500 kmph. If the speed of the product of combustion is Vpc, then V pc = Vpc-Vj = -1500 kmph (relative to the jet plane)

Speed of the combustion product relative to the observer on the ground,

Vpc = -1500 + Vj = -1500+500 = -1000 kmph

Q.3.6 A car moving along a straight highway with speed of 126 km h^–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?

Ans.3.6 The speed of the car = 126 kmph = (126 × 1000/3600) m/sec = 35 m/s

From the relation V² = U² + 2fs, where Final velocity V = 0, U = 35 m/s, s = 200m, we get retardation, f = -U²/2s= 3.06 m²/s

From the relation V = U – ft, we get t = U/f = 35/3.06 = 11.42 s.

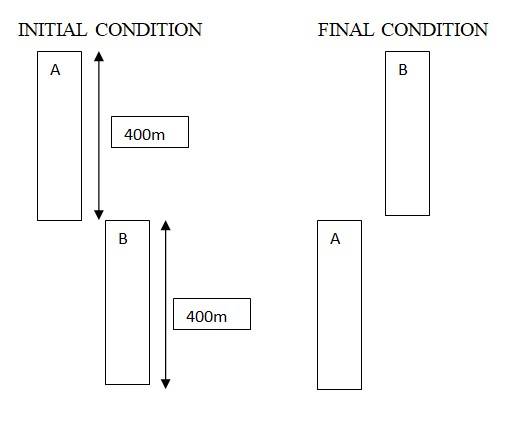
Q.3.7 Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h^–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m s^–2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?

Ans.3.7 The uniform speed of A and B = 72 kmph = 20 m/s

The acceleration f = 1 m/s², time t = 50 s,

Distance covered by train B = ut + 0.5 × ft²  = 20 × 50 + 0.5 × 1 × 50 ² = 2250 m

Distance covered by train A in the same period = ut = 50 × 20 = 1000 m

So the initial distance train A and train B was = 2250 – 1000 $–\left(400+400\right)$ = 450 m

Q.3.8 On a two lane road, car A is travelling with a speed of 36 km h^–1. Two cars B and C approach car A in opposite directions with a speed of 54 km h^–1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?

Ans.3.8

Speed of car A, Va = 36 kmph = 10m/s

Speed of car B , Vb = 54 kmph = 15 m/s

Speed of car C, Vc = -54 kmph = -15 m/s

Relative speed of A, w.r.t. C = Va – (-Vb) = 10 +15 = 25 m/s

Relative speed of B, w.r.t. A = Vb-Va = 15-10 = 5 m/s

Distance between AB & AC = 1 km = 1000m

Time taken by the car C to cover the distance AC, from s = ut

We get t = 1000/25 = 40s

To avoid collision with C, the minimum acceleration the vehicle B must have, from the relation, s = ut + (1/2) ft²

We get 1000 = 5 × 40 + (1/2) f × 40² f = 1 m/s²

Q.3.9 Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h^–1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?

Ans.3.9 Cycling speed  $V_c$ = 20 kmph

Let as assume speed of the bus is  $V_b$

The relative velocity of the buses in the direction of motion of the cyclist =  $V_b$ -  $V_c$

Buses go past him every 18 mins = 18/60h = 0.3h

Distance covered = (  $V_b-V_c$ ) × 0.3

Since the buses leave every T minutes, (  $V_b-V_c$ ) × 0.3 =  $V_b$ × (T/60) ……(1)

The relative velocity of the buses in the opposite direction of the cyclist =  $V_b$ +  $V_c$

Buses go past him in the opposite direction = every 6 m = 6/60 h

Distance covered = (  $V_b$ +  $V_c$ ) × 1/10

Since the buses leave every T minute, we get (  $V_b$ +  $V_c$ ) × 1/10 =  $V_b$ × T/60 …….(2)

From equations (1) & (2), we get

(  $V_b$ +  $V_c$ ) / 10 = (  $V_b-V_c$ ) × 0.3

$V_b$ +  $V_c$ = 3(  $V_b$ - 3  $V_c$ )

2  $V_b$ = 4  $V_c$ ,  $V_b$ = 2  $V_c$ So  $V_b$ = 2 × 20 = 40 kmph

From the equation (1), we get

(40-20) × 0.3 = 40 × T/60, T = 9 min

Q.3.10 A player throws a ball upwards with an initial speed of 29.4 m s^–1.

 (a) What is the direction of acceleration during the upward motion of the ball?

(b) What are the velocity and acceleration of the ball at the highest point of its motion?

(c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion.

(d) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s^–2 and neglect air resistance).

Ans.3.10 Due to gravity, the direction of acceleration will be always towards downwards

• At the highest point of its motion, the final velocity will be 0 and acceleration will be due to gravity 8 m s^–2
• If we consider the highest point x = 0 m, t= 0 s,

During upward motion of the ball before it reaches the maximum height, x = +ve, velocity = -ve, acceleration = +ve. During downward motion, x = +ve, velocity = +ve, acceleration = +ve

• At highest point, final velocity v = 0, initial velocity = 29.4 m/s, acceleration = 9.8m/s²

From the equation v2-u2 = 2gs, we get s = (29.4)²/2 × 9.8 = 44.1 m. From v –u = gt we get t = 29.4/9.8 s = 3 s. So the total time taken by the ball to reach player’s hand = 3 × 2s = 6 s

Q.3.11 Read each statement below carefully and state with reasons and examples, if it is true or false;

A particle in one-dimensional motion

(a) with zero speed at an instant may have non-zero acceleration at that instant

(b) with zero speed may have non-zero velocity,

(c) with constant speed must have zero acceleration,

(d) with positive value of acceleration must be speeding up.

Ans.3.11 True – zero speed may have a non zero instantaneous non-zero acceleration

False – zero speed will always make zero velocity

True – constant speed will have zero acceleration

False – If the positive value of acceleration is in the direction of its motion then it can speed up

Q.3.12 A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.

Ans.3.12 The initial velocity of the ball, u = 0

Height = 90 m

From v²-u² = 2as, we get v = $\sqrt[]{2\times g\times 90}$ = 42 m/s

Time taken for the first collision can be obtained from v = u + at, t = 42/g = 4.28 s

After first collision, ball looses 1/10 th of the velocity. So the rebound velocity = 0.9 × v = 37.8 m/s.

Time taken to reach the maximum height can be obtained from v = u + at

where v = 0. t = 37.8/9.81 = 3.853 s

Total time taken to reach the maximum height from beginning = 4.28 + 3.853 = 8.13 s

Now ball will again travel back to the ground at the same time it reach the maximum height = 3.853 s. So the total time taken will be = 4.28 +3.853 +3.853 = 11.986

Velocity after second collision = 0.9 × 37.8 = 34.02 m/s

So the graph can be plotted as

T           V

0           0

4.28      42

4.28       37.8

8.13       0

11.986   34.02

Q.3.13 Explain clearly, with examples, the distinction between:

(a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval;

(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval].

Show in both (a) and (b) that the second quantity is either greater than or equal to the first.

When is the equality sign true? [For simplicity, consider one-dimensional motion only].

Ans.3.13 Let us take the example of football world cup 2022. During Argentina match, Di Mario (A) passed the ball to Messi (B). Messi instantly passed the ball to Di Mario. Now the magnitude of displacement of the ball is 0 as the ball returns to Di Mario at the initial position. But the total length covered by the ball is AB + BA = 2AB. Hence total length covered by the particle (the ball) is more than the magnitude.

If t is the time taken to cover the entire distance, the magnitude of the average velocity of the ball over time interval t = Magnitude of displacement / t = 0 / t = 0

The average speed of the ball = Total length of the path / time interval = 2AB / t

Thus the second quantity is greater than the first.

If the ball moves only in one direction from A to B, both the quantities are equal (considering one-dimensional motion)

Q.3.14 A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h^–1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h^–1.

What is the

(a) magnitude of average velocity, and

(b) average speed of the man over the interval of time

 (i) 0 to 30 min,

(ii) 0 to 50 min,

(iii) 0 to 40 min?

[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]

Ans.3.14

The distance from home to market = 2.5 km = 2500 m

The speed of the walking while going = 5 kmph = 1.388 m/s

The speed of walking back from market to home = 7.5 kmph = 2.083 m/s

Magnitude of the average velocity = Displacement / time = 0, since the total displacement is zero.

Time taken to reach the market = distance / onward speed = 2500/1.388 = 1801 s = 30 minutes. So the average speed over 0 – 30 min is 5 kmph

Time taken to reach back home = 2500 / 2.083 = 20 minutes. So the average speed = total distance covered / total time taken = (2500 +2500)/(30 +20) m/min = 100 m/min = 6 kmph

Average speed over the interval of time 0 to 40 mins = Distance covered / time taken = 2500 + (2.083 × 10 × 600) /(40 × 60) = 1.5624 m/s = 5.62 kmph

Q.3.15 In Exercises 3.13 and 3.14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?

Ans.3.15 Instantaneous speed and velocity are applicable for a small interval of time because the magnitude of the displacement is effectively equal to the distance travelled by the particle.

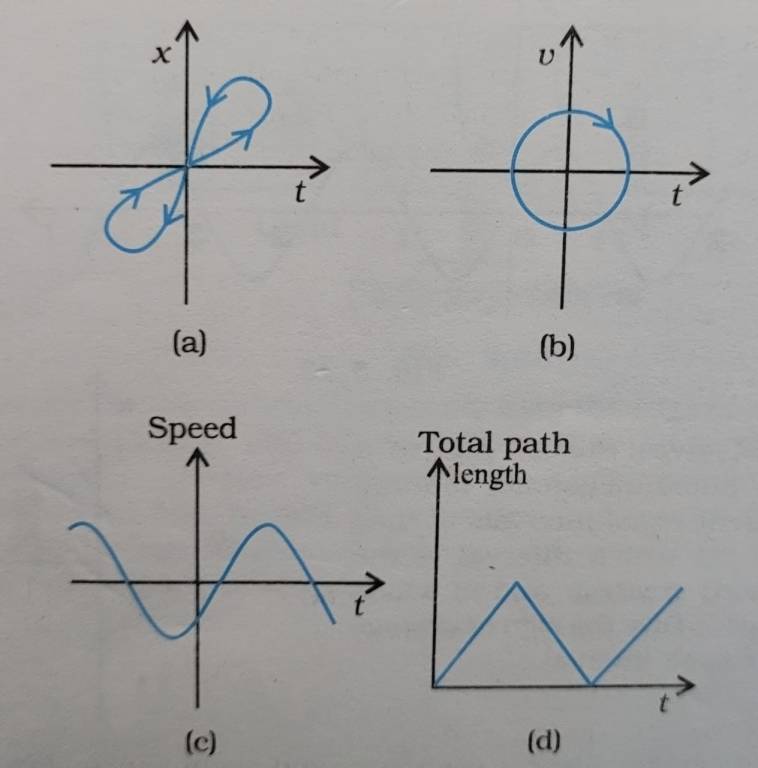
Q.3.16 Look at the graphs (a) to (d) (Fig. 3.20) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.

Ans.3.16 Figure (a) shows two positions at the same time, which is not possible for a one-dimensional motion.

A particle cannot have velocity in two directions at the same time in one-dimensional motion.

The graph shows negative speed, which is not possible because speed is always positive.

Total path length decreases, which is not possible for a one – dimensional motion.

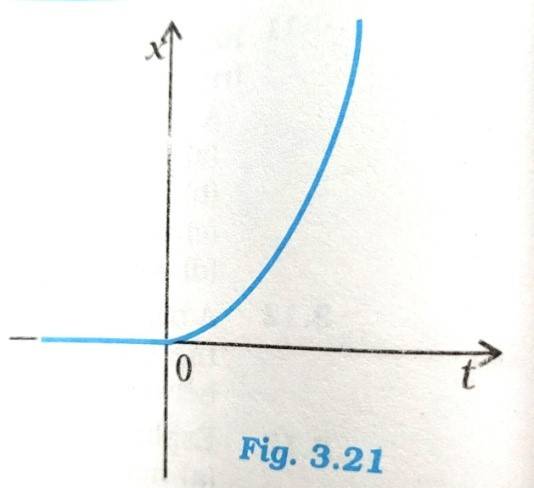
Q.3.17 Figure 3.21 shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t >0? If not, suggest a suitable physical context for this graph.

For t<0, we cannot say that the particle moved in a straight line and for t>0 on a parabolic path as the x-t graph does not indicate. Instead, this x-t graph denotes a particle is dropped from a height at t=0

Q.3.18 A police van moving on a highway with a speed of 30 km h^–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h^–1. If the muzzle speed of the bullet is 150 m s^–1, with what speed does the bullet hit the thief’s car?

(Note: Obtain that speed which is relevant for damaging the thief’s car).

Ans.3.18 Speed of the police van = 30 kmph = 8.33 m/s

Speed of the thief’s car = 192 kmph = 53.33 m/s

The muzzle speed of the bullet = 150 m/s

Speed of the bullet = speed of the police van + muzzle speed of the bullet = 8.33 + 150m/s = 158.33 m/s

The relative velocity of the bullet = speed of the bullet – speed of the thief’s car = 158.33 – 53.33 m/s = 105 m/s

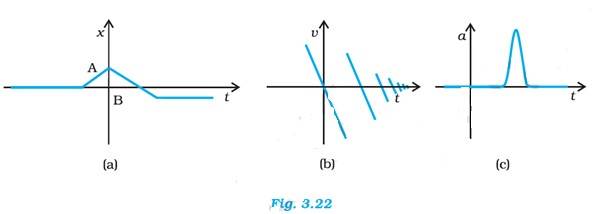
Q.3.19 Suggest a suitable physical situation for each of the following graphs (Fig 3.22):

Ans.3.19 The graph is similar to a carom board where the striker hits the edge, rebounds with reduced speed, then moves in the opposite direction, hits the opposite wall and stops.

This graph shows a situation where a ball falls on the ground from a certain height and rebounds with a reduced speed.

The situation is similar to a baseball, thrown on to a batter, moves with a uniform speed and then hit by a bat for a very short time interval.

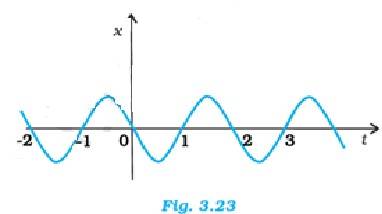
Q.3.20 Figure 3.23 gives the x-t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.

Ans.3.20 In simple harmonic motion, the acceleration is expressed as a = -  $\omega$ 2x, where  $\omega$ is the angular frequency.

At t = 0.3 s, position x is negative, velocity v is negative and acceleration a ( from above equation) will be positive

At t = 1.2 s, position x is positive, velocity is positive, acceleration a will be negative

At t = -1.2 s, position x is negative, velocity is positive and acceleration will be positive.

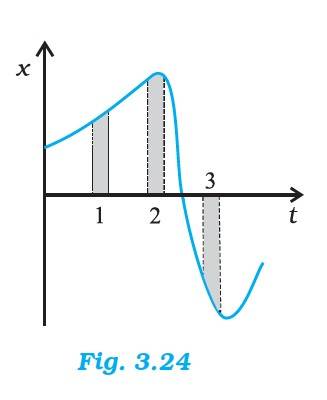
Q.3.21 Figure 3.24 gives the x-t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest, and in which is it the least? Give the sign of average velocity for each interval.

Ans.3.21 The average speed in Interval 3 is the greatest and in Interval 2 is the least.

The average velocity is +ve in Interval 1 & 2 and –ve in Interval 3.

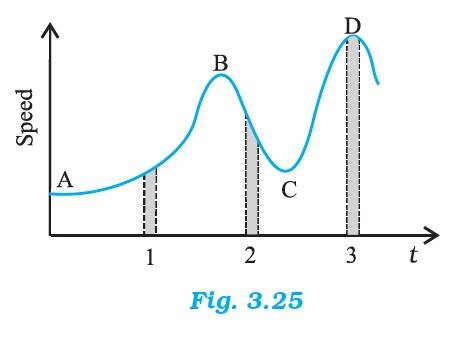
Q.3.22 Figure 3.25 gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

Ans.3.22 The change in the speed with time is maximum in interval 2. Therefore, the average acceleration is greatest in magnitude in interval 2.

The average speed is maximum in interval 3.

The sign of velocity is positive in intervals 1,2 and 3.

Acceleration depends on the slope. The acceleration is positive in interval 1 and 3, as the slope is positive. The acceleration is negative in interval 2, as the slope is negative.

Acceleration at A, B, C and D is zero since the slope is parallel to the time axis at these instants.

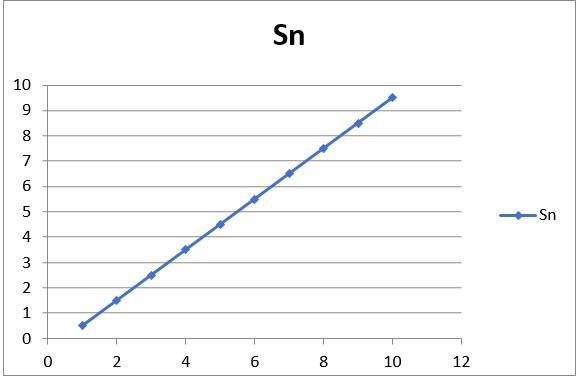
Q.3.23 A three-wheeler starts from rest, accelerates uniformly with 1 m s^–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?

Ans.3.23 The distance covered by the 3 wheeler on a straight line in the nth second can be expressed as:

Sn = u + a(2n-1)/2 ……(1),

Where

a = acceleration

u = initial velocity

n = time = 1,2,3,……..,n

Given, u = 0, a = 1m/s², from equation (1) we get Sn = (2n-1)/2 ……..(2)

With various values of n, we get Sn

            n                      Sn

            1                      0.5

            2                      1.5

            3                      2.5

            4                      3.5

            5                      4.5

            6                      5.5

            7                      6.5

            8                      7.5

            9                      8.5

            10                    9.5

Q.3.24 A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m s^–1. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m s^-1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?

Ans.3.24 The initial velocity of the ball, u = 49m/s

First Case: When the ball returns to his hands, total displacement = 0

From the relation s = ut + 0.5at², we get 0 = 49t + 0.5 (-9.81) t²

                                                      4.905 = 49t      Hence t = 10s

Second Case:

As the lift started moving up with a speed of 5 m/s, the initial velocity of the ball = 49 + 5 m/s = 54 m/s

If t’ is time for the ball to return to his hand, the displacement of the ball will be = 5t’

From the relation        s = ut + 0.5 x at², we get

                                    5t’ = 54t’ + 0.5 × (-9.8) t’²

                                                      49t’ = 4.9 t’²

            t’ = 10 s       

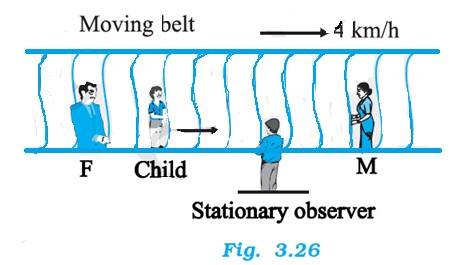
Q.3.25 On a long horizontally moving belt (Fig. 3.26), a child runs to and fro with a speed 9 km h ^–1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h^–1. For an observer on a stationary platform outside, what is the

(a) speed of the child running in the direction of motion of the belt?

(b) speed of the child running opposite to the direction of motion of the belt?

(c) time taken by the child in (a) and (b)?

Which of the answers alter if motion is viewed by one of the parents?

Ans.3.25 Speed of the child = 9 km/h

Speed of belt = 4 km/h

When the boy runs in the direction of motion of the belt, then the speed of the child observed by the stationary observer = 9 + 4 = 13 km/h

When the boy runs in the opposite direction of motion of the belt, then the speed of the child observed by the stationary observer = 9-4 = 5 km/h

Distance between the parents = 50 m = 0.05km

Speed of the boy, as observed by both parents = 9 km/h.

Time required by the boy to move to any parent = 0.05 / 9 h = 20s

 

Q.3.26 Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m s^–1 and 30 m s^–1. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m s^–2. Give the equations for the linear and curved parts of the plot.

Ans.3.26 For the first stone,

Initial velocity, u₁ = 15m/s, acceleration, a = -g = -10 m/s

From the relation  s₁=s₀+u₁t+(1/2)at² where

s₀ = cliff height, s₁ = total height of the fall of the first stone, we get

s₁ = 200 + 15t – 5t²  ………..(1)

When the stone hit the floor , s₁ = 0, so the equation (1) becomes

0 = 200 +15t - 5t² = t² -3t – 40 = (t-8)(t+5) = 0

So t = 8s or -5s

Since the stone was thrown at t=0, so t cannot be –ve. Hence t = 8s

For the second stone,

Initial velocity, u₁ = 30 m/s, acceleration, a = -g = -10 m/s

From the relation  s₂=s₀+u₁t+(1/2)at² where

s₀ = cliff height, s₂= total height of the fall of the second stone, we get

s₂ = 200 + 30t – 5t²  ………..(2)

When the stone hit the floor , s₂ = 0, so the equation (2) becomes

0 = 200 +30t - 5t² = t² -6t – 40 = (t-10)(t+4) = 0

So t = 10s or -4s

Since the stone was thrown at t=0, so t cannot be –ve. Hence t = 10s

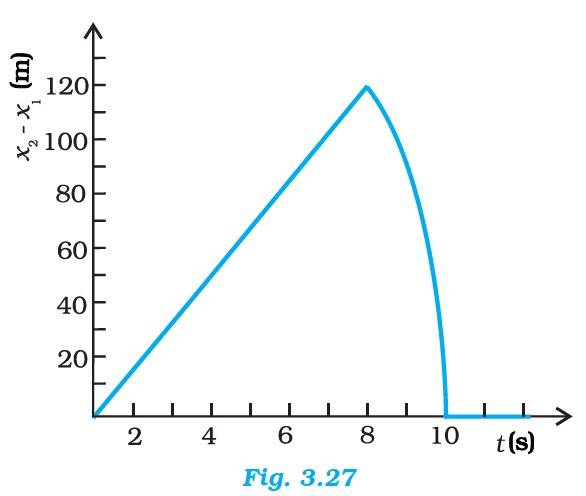
Subtracting equation (1) from equation (2), we get

s_{2 –} s₁ = (200 + 30t – 5t²  ) – (200 + 15t – 5t² )  = 15t ……..(3)

Equation (3) represents the linear trajectory of the two stones because to this linear relation between (s_{2 –} s₁₎ and t, the projection is straight line till 8s (from the graph)

The maximum distance between the two stones is at t = 8s. So

(s_{2 –} s₁) _max = 15 x 8 = 120 m. This value has been depicted correctly in the graph.

After 8s, only the second stone is in motion (t for first stone has been found out to be 8s), the trajectory of second stone is obtained in equation (2), = 200 + 30t – 5t²  , which is a curved path.

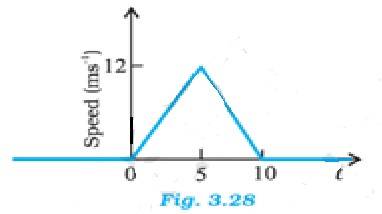
Q.3.27 The speed-time graph of a particle moving along a fixed direction is shown in Fig. 3.28. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s, (b) t = 2 s to 6 s.

 

Ans.3.27 Distance travelled by the particle between t = 0 s and t = 10 s is the area of the triangle = (1/2) x base x height = (1/2) x 10 x 12 = 60 m

The average speed of the particle is 60/10 m/s = 6 m/s

 

• Distance travelled by the particle between t = 2 s and t = 6 s

Let S₁ be the distance travelled by the particle in time 2 to 5 s and S₂ be the distance travelled between 5 to 6s.

For the motion  from 0 to 5 sec, u = 0, t = 5, v = 12 m/s

From the equation v = u + at we get a = (v-u)/t = 12/5 = 2.4 m/s²

Distance covered from 2 to 5 sec, S₁ = distance covered in 5 s – distance covered in 2 s

From the equation s = ut + at² we get,

= (1/2) × 2.4 × 25 – (1/2) × 2.4 × 4 = 30 – 4.8 = 25.2 m

For the motion from 5 sec to 10 sec, u = 12 m/s and a = -2.4 m/s²

and t = 5 sec to t = 6 sec means n = 1 for this motion

Distance covered in the 6th sec is S2 = u + (1/2) a (2n-1) = 12 + (1/2) (-2.4) (2 × 1-1) = 10.8 m

Therefore the total distance covered from t = 2 to 6 s = 25.2 + 10.8 m = 36 m

 

Q.3.28 The velocity-time graph of a particle in one-dimensional motion is shown in Fig 3.29 :

Which of the following formulae are correct for describing the motion of the particle

over the time-interval t₁ to t₂:

(a) x(t₂ ) = x(t₁) + v (t₁) (t₂ – t₁) +(½) a (t₂ – t₁)²

(b) v(t₂ ) = v(t₁) + a (t₂ – t₁)

(c) v_average = (x(t₂) – x(t₁))/(t₂ – t₁)

(d) a_average = (v(t₂) – v(t₁))/(t₂ – _t1)

(e) x(t₂ ) = x(t₁) + v_average (t₂ – t₁) + (½) a_average (t₂ – t₁)²

(f) x(t₂ ) – x(t₁) = area under the v-t curve bounded by the t-axis and the dotted line

shown.

Ans.3.28 The graph has a non-uniform slope between the intervals t₁ and t₂ – the graph is not a straight line. The equations (a), (b), and (e) do not describe the motion of the particle. Only the relations (c), (d) and (f) are correct.