Thermal Properties of Matter Class 11 NCERT Solutions: Download Questions & Answers PDF

• Introduction to Thermal Properties of Matter
• Temperature and heat
• Measurement of temperature
• Ideal-gas equation and absolute temperature
• Thermal expansion
• Specific heat capacity
• Calorimetry
• Change of state
• Heat transfer

Newton’s law of cooling

Thermal Properties of Matter Class 11 NCERT solutions PDF according to the latest CBSE syllabus are available for free download. The Physics NCERT Class 11 PDF download can be kept for future reference. The PDF form of the solutions can be opened and checked by the students even if there is no access to the internet.

Download Here: NCERT Solution for Class XI Physics Chapter Thermal Properties of Matter PDF

Q.11.1 The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.

Ans.11.1 Kelvin and Celsius scales are related as

$T_c$ =  $T_k$ - 273.15 …..(i),

where  $T_c=$ temperature in Celsius scale and  $T_k$ = temperature in Kelvin scale

Celsius and Fahrenheit scales are related as

$\frac{T_c\mathrm{}}{5}$ =  $\frac{T_f-32}{9}$ , where  $T_f$ = temperature in Fahrenheit scale

For Neon,  $T_k$ = 24.57. Hence  $T_c$ = 24.57 – 273.15 = -248.58 degree Celsius

$T_f=\frac{9}{5}\times T_c+32$ =  $\frac{9}{5}\times (-248.58)+32$ = -415.44 degree Fahrenheit

For Carbon dioxide,  $T_k$ = 216.55. Hence  $T_c$ = 216.55 – 273.15 = -56.6 degree Celsius

$T_f=\frac{9}{5}\times T_c+32$ =  $\frac{9}{5}\times (-56.6)+32$ = -69.88 degree Fahrenheit

 

Q.11.2 Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B ?

Ans.11.2 Triple point of water on absolute scale A,  $T_1$ = 200 A

Triple point of water on absolute scale B,  $T_2$ = 350 B

Triple point of water on absolute Kelvin scale,  $T_k$ = 273.15 K

The temperature 273.15 K on Kelvin scale is equivalent to 200 on absolute scale A

$T_1=T_k$

200 A = 273.15 K , Therefore A =  $\frac{273.15}{200}$

Similarly B =  $\frac{273.15}{350}$

If  $T_A$ is the triple point of water on scale A and  $T_B$ is the triple point of water on scale B, we have

$\frac{273.15}{200}$  $\times T_A$ =  $\frac{273.15}{350}\times$  $T_B$

$T_A=$  $\frac{200}{350}\times$  $T_B$ =  $\frac{4}{7}\times$  $T_B$

 

Q.11.3 The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law :

R = Ro [1 + α(T –  ${\mathit{T}}_0$ )]

The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?

Ans.11.3: It is given that R =  $R_0$ [1 + α(T –  $T_0$ )] ………(i)

Where Ro and To are the initial resistance and temperature and R and T are the final resistance and temperature.

At the triple point of water, To = 273.15 K,  $R_0$ = 101.6 Ω

At normal melting point of lead, T = 600.5 K, R = 165.5 Ω

Substituting these values in equation (i), we get

165.5 =  $101.6$ [1 + α(600.5 –  $273.15$ )]

$\frac{165.5}{101.6}$ = 1 + 327.35 α, or α =  $\frac{0.629}{327.35}$ = 1.92  $\times {10}^{-3}$  $K^{-1}$

When R = 123.4 Ω, T can be calculated as

123.4 =  $101.6$ [1 + 1.92  $\times {10}^{-3}\times$ (T –  $273.15$ )]

1.214 = 1 + T1.92  $\times {10}^{-3}$ - 1.92  $\times {10}^{-3}\times$ 273.15

T = 384.6 K

 

Q.11.4 Answer the following :

(a) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale) ?

(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale ?

(c) The absolute temperature (Kelvin scale) T is related to the temperature  ${\mathit{t}}_{\mathit{c}}$ on

the Celsius scale by  ${\mathit{t}}_{\mathit{c}}$ = T – 273.15

Why do we have 273.15 in this relation, and not 273.16 ?

(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?

Ans.11.4 The triple point of water has a unique value of 273.16 K, irrespective of pressure and volume. Whereas, melting point of ice and boiling point of water, the temperature value depends on pressure and volume.

The other fixed point on Kelvin scale is 0 K.

The temperature 273.16 K is the triple point of water, it is not the melting point of ice. The melting point of ice is specified in Celsius scale as 0  $°C.$ Hence the absolute temperature in Kelvin scale,  $T_k$ is related to temperature  $T_c$ in Celsius scale as

$T_c=T_k-273.15$

Let  $T_f$ and  $T_k$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_f-32}{9}$ =  $\frac{T_k-273.15}{5}$ ……(i)

Let  $T_{f1}$ and  $T_{k1}$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_{f1}-32}{9}$ =  $\frac{T_{k1}-273.15}{5}$ ……(ii)

It is given  $T_{k1}-T_k$ = 1 K

Now subtracting (i) from (ii), we get

$\frac{T_{f1}-32}{9}$ -  $\frac{T_f-32}{9}$ =  $\frac{T_{k1}-273.15}{5}-\frac{T_k-273.15}{5}$

$\frac{T_{f1}-T_f}{9}$ =  $\frac{T_{k1}-T_k}{5}$

$T_{f1}-T_f$ =  $\frac{9}{5}$

Triple point of water = 273.16 K

Hence triple point of water in the absolute scale = 273.16  $\times$  $\frac{9}{5}$ = 491.69

 

Q.11.5 Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made:

Temperature                         Pressure                     Pressure

thermometer A          thermometer B

Triple-point of water            1.250 × 10⁵ Pa            0.200 × 10⁵ Pa

Normal melting point           1.797 × 10⁵ Pa            0.287 × 10⁵ Pa

of sulphur

(a) What is the absolute temperature of normal melting point of sulphur as read by thermometers A and B ?

(b) What do you think is the reason behind the slight difference in answers of thermometers A and B? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?

Ans.11.5 FOR THERMOMETER A

Triple point of water, T = 273.16 K

At this temperature, the pressure in thermometer A ,  $P_A$ = 1.250  $\times {10}^5$ Pa

Let  $T_1$ be the temperature for the normal melting point of sulphur and  $P_1$ be the corresponding pressure. It is given,  $P_1$ = 1.797  $\times {10}^5$ Pa

From Charles’ law, we get  $\frac{P_A}{T}$ =  $\frac{P_1}{T_1}$ ,  $T_1$ =  $\frac{P_1\times \mathrm{T}}{P_A}$ =  $\frac{1.797\mathrm{}\times {10}^5\times 273.16}{1.250\mathrm{}\times {10}^5}$ = 392.69 K

FOR THERMOMETER B

Triple point of water, T = 273.16 K

At this temperature, the pressure in thermometer B ,  $P_B$ = 0.2  $\times {10}^5$ Pa

Let  $T_1$ be the temperature for the normal melting point of sulphur and  $P_1$ be the corresponding pressure. It is given,  $P_1$ = 0.287  $\times {10}^5$ Pa

From Charles’ law, we get  $\frac{P_B}{T}$ =  $\frac{P_1}{T_1}$ ,  $T_1$ =  $\frac{P_1\times \mathrm{T}}{P_B}$ =  $\frac{0.287\mathrm{}\times {10}^5\times 273.16}{0.2\mathrm{}\times {10}^5}$ = 391.98 K

The oxygen and hydrogen gas present in thermometers A and B respectively are not perfect ideal gas, hence there is a slight difference in readings.

To reduce the difference between two readings, the measurement should be carried out at low pressure so that gases behave like an ideal gas.

 

Q.11.6 A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day ? What is the length of the same steel rod on a day when the temperature is 27.0 °C ? Coefficient of linear expansion of steel = 1.20 × 10^–5 K^–1 .

Ans.11.6 Length of the steel tape, l = 1 m = 100 cm, At temperature T = 27  $°$ C

Coefficient of linear expansion of steel  $\alpha$ = 1.2  $\times {10}^{-5}$ / K

Let  $l_1=63cm$ be the length of the steel rod at temperature  $T_1$ = 45.0 °C and

$l_2$ be the length of the steel rod and l’ be the length of the steel tape at 45.0 °C

We have l’ = l +  $\alpha l(T_1-T)$ = 100 + 1.2  $\times {10}^{-5}\times 100\times$ (45-27) = 100.0216 cm

$l_2$ can be calculated as  $l_2$ =  $\frac{l\text{'}}{l}\times 63$ = 63.0136 cm

 

Q.11.7 A large steel wheel is to be fitted on to a shaft of the same material. At 27 °C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range :  ${\mathit{\alpha }}_{\mathit{s}\mathit{t}\mathit{e}\mathit{e}\mathit{l}}$ = 1.20× ${10}^{-5}$  ${\mathit{K}}^{-1}$

Ans.11.7: Given, temperature  $T_1$ = 27 °C = 27 + 273.16 K = 300.16 K

Outer dia of the shaft at temp  $T_1$ ,  $d_1$ = 8.7 cm

Diameter of the central hole of the wheel,  $d_2$ = 8.69 cm

The change in diameter, Δd=  $d_2-d_1=$ 8.69 – 8.7 =  $-$ 0.01 cm

After the shaft is cooled in dry ice, its temperature becomes  $T_2$ . It can be calculated from the relation

Δd=  $d_1\times {\alpha }_{steel}$ (  $T_2-T_1)$

-0.01 = 8.7  $\times 1.20\mathrm{}\times \mathrm{}{10}^{-5}(T_2-300)$

$T_2-300$ = -95.78

$T_2$ = 204.22 K = -68.94  $℃$

 

Q.11.8 A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C?

Coefficient of linear expansion of copper = 1.70 × 10^–5 K^–1.

Ans.11.8 Initial temperature,  $T_1$ = 27.0 °C, Initial diameter of the hole,  $d_1$ = 4.24 cm

Final temperature,  $T_2$ = 227.0 °C, Final diameter of the hole  $=d_2$

Coefficient of linear expansion of copper,  ${\alpha }_{copper}$ = 1.70  $\times {10}^{-5}$ K–1

We know

$\frac{Changeinarea(∆A)}{Originalarea\left(A\right)}$ =  $\beta ∆$ T where  $\beta$ is the coefficient of superficial expansion,  $\beta =2{\alpha }_{copper}$

$\frac{(\mathit{\pi }\frac{{\mathit{d}}_2^2}{4}-\mathit{}\mathit{\pi }\frac{{\mathit{d}}_1^2}{4})}{\mathit{\pi }\frac{{\mathit{d}}_1^2}{4}}$ =  $2{\alpha }_{copper}∆$ T

$\frac{{\mathit{d}}_2^2-\mathit{}{\mathit{d}}_1^2}{{\mathit{d}}_1^2}$ =  $2{\alpha }_{copper}∆$ T

$\frac{{\mathit{d}}_2^2}{{\mathit{d}}_1^2}$ - 1=  $2{\alpha }_{copper}\left(T_2-T\right)=$ 2  $\times$ 1.70  $\times {10}^{-5}$ (227-27) = 6.8  $\times {10}^{-3}$

$d_2^2=1.0068\times 4.24\times 4.24$

$d_2$ = 4.2544 cm

So change in diameter = 4.2544 – 4.24 = 0.01439 cm

Diameter increase by 1.44  $\times {10}^{-2}$ cm

 

Q.11.9 A brass wire 1.8 m long at 27°C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of –39 °C, what is the tension developed in the wire, if its diameter is 2.0 mm ? Co-efficient of linear expansion of brass = 2.0 × 10^–5 K–1; Young’s modulus of brass = 0.91 × 10¹¹ Pa.

Ans.11.9 Initial temperature, $T_1$ = 27°C, Length of the wire  $l_1$ at  $T_1$ = 1.8 m

Final temperature,  $T_2$ = -39°C

Diameter of the wire, d = 2.0 mm = 2  $\times {10}^{-3}$ m

Coefficient of linear expansion of brass,  $\alpha =2\times {10}^{-5}$ /K

Youngs’ modulus of brass, Y = 0.91  $\times {10}^{11}$ Pa

Let the tension developed be F

We know Youngs’ modulus =  $\frac{Stress}{Strain}$ =  $\frac{\frac{F}{A}}{\frac{∆L}{L}}=Y$

Y  $\times \frac{∆L}{L}$ =  $\frac{F}{A}$ or F =  $\frac{AY∆L}{L}$

Here, A = cross-sectional area of the wire =  $\frac{\pi }{4}{d}^2$ =  $\frac{\pi }{4}{(2\mathrm{}\times {10}^{-3})}^2$  $m^2$ = 3.1416  $\times {10}^{-6}{m}^2$

Now  $∆L$ can be written as  $∆L$ =  $\alpha L(T_2-\mathrm{}{T}_1)$ = (  $2\times {10}^{-5})\times L\times (-39-27)$ = -1.32  $\times {10}^{-3}$ L

Substituting all values, we get

F = (3.1416  $\times {10}^{-6}\times 0.91\mathrm{}\times {10}^{11}\times (-1.32\times {10}^{-3})$ = -377.37 N

 

Q.11.10 A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction ? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10^–5 K^–1, steel = 1.2 × 10^–5 K^–1 ).

Ans.11.10 Initial temperature,  $T_1$ = 40.0°C, Final temperature,  $T_2$ = 250°C,  $∆$ T =  $T_2$ -  $T_1$ = 210°C

Initial length of the brass rod at  $T_1$ ,  $l_b$ = 50 cm, Initial diameter of the brass rod at  $T_1$ ,  $d_1$ = 3 mm

Length of the steel rod  $l_s=50cm$

For the expansion of the brass rod, we have:

$\frac{Changeinlength(∆l_{b)}}{Originallength(l_{b)}}$ =  ${\alpha }_b∆T$ , then  $∆l_b$ = 50  $\times 2.0\mathrm{}\times \mathrm{}{10}^{-5}\times 210$ = 0.21 cm

For the expansion of the steel rod, we have:

$\frac{Changeinlength(∆l_{s)}}{Originallength\left(l_s\right)}$ =  ${\alpha }_b∆T$ , then  $∆l_s$ = 50  $\times 1.2\mathrm{}\times \mathrm{}{10}^{-5}\times 210$ = 0.126 cm

Total change in length = 0.21 + 0.126 = 0.336 cm

Since the rods are free at the end, no thermal stress developed.

 

Q.11.11 The coefficient of volume expansion of glycerin is 49 × 10^–5 K^–1. What is the fractional change in its density for a 30 °C rise in temperature ?

Ans.11.11 Coefficient of volume expansion of glycerin,  ${\alpha }_V$ = 49  $\times {10}^{-5}$ /K

Rise in temperature,  $∆T$ = 30°C

Fractional change in volume =  $\frac{∆V}{V}$

We can write,  $\frac{∆V}{V}$ =  ${\alpha }_V\times ∆T$ = 49  $\times {10}^{-5}\times 30$ = 0.0147 ……(i)

If the final volume is  $V_2$ and initial volume is  $V_1$ , then

$\frac{∆V}{V}$ =  $\frac{V_2-V_1}{V_1}$

$V_2=\frac{m}{{\rho }_2}$ and  $V_1=\frac{m}{{\rho }_1}$ where  ${\rho }_1$ &  ${\rho }_2$ are initial and final densities

$\frac{∆V}{V}$ =  $\frac{V_2-V_1}{V_1}$ =  $\frac{{\rho }_2-{\rho }_1}{{\rho }_1}$ = fractional change in density = 0.0147 = 1.47  $\times$  ${10}^{-2}$

 

Q.11.12 A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings. Specific heat of aluminium = 0.91 J g^–1 K^–1.

Ans.11.12 Power of the drilling machine, P = 10 kW= 10  $\times {10}^3$ W

Mass of the Aluminium block, m = 8.0 kg = 8  $\times {10}^3$ gm

Time for which the machine is used, t = 2.5 minute = 2.5  $\times 60$ s = 150 s

Specific heat of Aluminium, c = 0.91 J/gK

Let the rise of temperature in the block after drilling be  $\delta$ T

Total energy consumed by the drilling machine= P  $\times t$ = 10  $\times {10}^3\times 150$ J = 1.5  $\times {10}^6$ J

It is given 50% of energy is useful.

So useful energy,  $∆Q$ = 50% of Pt= 0.5  $\times$ 1.5  $\times {10}^6=$ 7.5  $\times {10}^5$ J

We know,  $∆Q$ = mc  $∆$ T or T =  $\frac{∆Q}{mc}$ =  $\frac{7.5\mathrm{}\times {10}^5}{8\mathrm{}\times {10}^3\times 0.91}$ = 103  $℃$

Therefore 2.5 minute drilling will raise the block temperature by 103  $℃$

 

Q.11.13 A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500 °C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39 J g^–1 K^–1; heat of fusion of water = 335 J g^–1 ).

Ans.11.13 Mass of the copper block, m = 2.5 kg = 2.5  $\times {10}^3$ gm

Rise in temperature of the copper block,  $∆$ T = 500°C

Specific heat of the copper, C = 0.39 g–1 K–1

Heat of fusion of water, L = 335 J g–1

The maximum heat the copper block can lose, Q = mc  $∆$ T = 2.5  $\times {10}^3\times 0.39\times 500$ = 487500 J

Let  $m_1$ gm be the mass of the ice, which will melt because of the copper block.

Heat gained by ice block = Q =  $m_{1}L$

$m_1=\frac{Q}{L}$ =  $\frac{487500}{335}$ g = 1455.22 gm = 1.45 kg

 

Q.11.14 In an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150 °C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27 °C. The final temperature is 40 °C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal?

Ans.11.14 Mass of the metal, m = 0.20 kg = 200 g

Initial temperature of the metal,  $T_1$ = 150 °C, Final temperature of the metal,  $T_2$ = 40 °C

The water equivalent mass of the calorimeter, m’ = 0.025 kg = 25 g

Volume of water, V = 150 cm3

Mass of water, M at T = 27 °C, = 150  $\times 1=150g$

Fall in metal temperature,  $∆$ T =  $T_1-T_2$ = 150 – 40 = 110 °C

Specific heat of water,  $C_w$ = 4.186 J/g/  $°$ K

Let the specific heat of metal = C

Then, heat loss by the metal,  $\theta$ = mC  $∆$ T …….(i)

Rise in the water of the calorimeter system  $∆$ T’ = 40 – 27 = 13°C

Heat gained by the water and calorimeter system;  $\theta \text{'}$ = (M + m’)  $C_w∆$ T’ ……(ii)

Now heat lost by the metal = heat gained by the water and calorimeter system

mC  $∆$ T = (M + m’)  $C_w∆$ T’

C =  $\frac{(\mathrm{M}\mathrm{}+\mathrm{}\mathrm{m}\mathrm{’})C_w∆\mathrm{T}\mathrm{’}}{m∆\mathrm{T}}$ =  $\frac{(150+25)\times 4.186\times 13}{200\times 110}$ = 0.433 J/g/  $°$ K

 

Q.11.15 Given below are observations on molar specific heats at room temperature of some common gases.

Gas                                         Molar specific heat (Cv )

                                                (cal mo1^–1 K^–1)

Hydrogen                               4.87

Nitrogen                                 4.97

Oxygen                                   5.02

Nitric oxide                            4.99

Carbon monoxide                 5.01

Chlorine                                 6.17

The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine ?

Ans.11.15 The gases listed above are diatomic. Besides the translational degree of freedom, they have other degrees of freedom. Heat must be supplied to increase the temperature of these gases. This increases the average energy of all the modes of motion. Hence the molar specific heat of diatomic gases is more than that of monatomic gases.

If only rotational mode of motion considered, then the molar specific heat of a diatomic gas

=  $\frac{5}{2}$ R =  $\frac{5}{2}\times 1.98$ = 4.95 cal mo1^–1 K^–1

With the exception of Chlorine, all the observations given above agrees with (  $\frac{5}{2}$ R). This is because at room temperature, chlorine also has vibrational modes besides rotational and translational modes of motion.

 

Q.11.16 A child running a temperature of 101°F is given an antipyrin (i.e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to 98°F in 20 minutes, what is the average rate of extra evaporation caused, by the drug. Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of human body is approximately the same as that of water, and latent heat of evaporation of water at that temperature is about 580 cal g ^–1.

Ans.11.16 Initial body temp of the child,  $T_1$ = 101°F

Final body temp of the child,  $T_2$ = 98°F

Change in temperature,  $∆$ T =  $T_1-T_2=(101°\mathrm{F}-\mathrm{}$ 98°F) = 3 °F =  $\frac{5}{9}$ (3-32)  $°$ C = 1.666  $℃$

Time taken t achieve this temperature, t = 20 min

Specific heat of human body = Specific heat of water, c = 1000 cal/kg/  $℃$

Latent heat of evaporation of water, L = 580 cal/g

Mass of the child, m = 30 kg

The heat lost by the child is given as  $∆\theta =mc∆\mathrm{T}$ = 30  $\times 1000\times 1.666$ = 49980 cal

Let  $m_1$ be the mass of water evaporated from the child’s body in 20 mins.

Loss of heat  $∆\theta$ =  $m_1\times L$ = 580  $m_1$ =  $49980cal$

$m_1=$ 86.2 gm

Rate of evaporation =  $\frac{m_1}{t}$ = 4.31 g/min

 

Q.11.17 A ‘thermacole’ icebox is a cheap and an efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side 30 cm has a thickness of 5.0 cm. If 4.0 kg of ice is put in the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45 °C, and co-efficient of thermal conductivity of thermacole is 0.01 J s–1 m–1 K–1. [Heat of fusion of water = 335 × 103 J kg–1]

Ans.11.17 Size of the sides of cubical ice box, s = 30 cm =0.3 m

Thickness of the icebox, l = 5 cm = 0.05 m

Mass of ice kept in the box, m = 4 kg

Time gap , t = 6 h = 6  $\times 60\times 60$ s

Outside temperature, T = 45 °C

Coefficient of thermal conductivity of thermocole, K = 0.01 J  $s^{-1}{m}^{-1}{K}^{-1}$

Heat of fusion of water, L = 335  $\times {10}^3$ J  ${kg}^{-1}$

Let m’ be the mass of the ice melts in 6 h

The amount of heat lost by the food:  $\theta$ =  $\frac{KA\left(T-0\right)t}{l}$ ,where

A = Surface area of the box = 6  $s^2$ = 6  $\times {0.3}^2{m}^2$ = 0.54  $m^2$

$\theta$ =  $\frac{0.01\times 0.54\left(45-0\right)\times 6\mathrm{}\times 60\times 60}{0.05}$ = 104976 J

We also know  $\theta =m\text{'}L$ so m’ = 104976/(335  $\times {10}^3)$ = 0.313 kg

Hence the amount of ice remains after 6 h = 4 – 0.313 = 3.687 kg

 

Q.11.18 A brass boiler has a base area of 0.15 m² and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass = 109 J s^–1 m^–1 K^–1 ; Heat of vaporization of water = 2256 × 10³ J kg^–1.

Ans.11.18 Base area of the boiler, A = 0.15 m2

Thickness of the boiler, l = 1.0 cm = 0.01 m

Boiling rate of water, R = 6.0 kg/min

Let us assume the mass of the boiling water, m = 6 kg and the time to boil, t = 1 min = 60 s

Thermal conductivity of brass, K = 109 J s–1 m–1 K–1

The amount of heat flowing into water through the brass base of the boiler is given by:

$\theta$ =  $\frac{KA\left(T_1-T_2\right)t}{l}$ , where

$T_1$ = Flame temperature in contact with the boiler

$T_2$ = Boiling point of water = 100  $℃$

Heat required for boiling water  $\theta$ = mL, where L = heat of vaporization of water = 2256 × 103 J kg–1

By equating for  $\theta$ we get

6  $\times 2256\times {10}^3$ = 109  $\times 0.15\times \left(T_1-T_2\right)\times 60/0.01$

$\left(T_1-T_2\right)$ = 137.98  $℃$

$T_1$ = 237.98  $℃\left(\mathrm{F}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{b}\mathrm{o}\mathrm{i}\mathrm{l}\mathrm{e}\mathrm{r}\right)$

 

Q.11.19 Explain why :

(a) a body with large reflectivity is a poor emitter

(b) a brass tumbler feels much colder than a wooden tray on a chilly day

(c) an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace

(d) the earth without its atmosphere would be inhospitably cold

(e) heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water

Ans.11.19 A body with a large reflectivity is a bad absorber. A bad absorber will in turn be a poor emitter of radiations.

Brass is a good conductor of heat, when one touches a brass tumbler, heat is conducted from the body to the brass tumbler easily. Hence, the temperature of the body reduces to a colder value and one feels cold.

On the other hand, wood is a poor conductor of heat. Very little heat is conducted from the body to the wooden tray. Resulting in negligible drop in body temperature.

Thus a brass tumbler feels colder than a wooden tray on a chilly day.

Black body radiation equation is given by:

E =  $\sigma$ (  $T^4$ -  $T_o^4$ ), where

E = energy radiation

$\sigma$ = constant

$T=$ temperature of the optical pyrometer

$T_o$ = Temperature of open space

$\mathrm{H}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{}\mathrm{}\mathrm{a}\mathrm{n}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{}\mathrm{i}\mathrm{n}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{}\mathrm{o}\mathrm{f}\mathrm{}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{}\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}$

When the same piece of iron placed in a furnace, the radiation energy is E = $\sigma T^4$

In the absence of atmospheric gases, no extra heat will be trapped. All the heat would be radiated back from Earth’s surface.

A heating system based on the circulation of steam is more efficient in warming a building than that based on the circulation of hot water. This is because steam contains surplus heat in the form of latent heat ( 540 cal/g)

 

Q.11.20 A body cools from 80 °C to 50 °C in 5 minutes. Calculate the time it takes to cool from 60 °C to 30 °C. The temperature of the surroundings is 20 °C.

Ans.11.20 According to Newton’s law of cooling, we have   = K(T - $T_o$ ) or $\frac{dT}{K(T\mathrm{}-\mathrm{}{T}_o)}$ = -Kdt……(i)Where, temperature of the body = T

Temperature of the surroundings = $T_o$ = 20 °C

K is a constant

The temperature of the body falls from 80 $℃$  ${\mathrm{<br>}}_{}$ to 50 $℃intimet=5\min =300s$

Integrating equation (i), we get

$\mathrm{<br>}$ $\underset{80}{\overset{}{50}}\frac{dT}{K(T\mathrm{}-\mathrm{}{T}_o)}$ = - ${\int }_0^{300}Kd\mathrm{t\int }$ $\underset{}{\overset{}{\mathrm{<br>}}}$

${<br>}_{}^{}$ $\mapsto {\left[{\log }_e(T\mathrm{}-\mathrm{}{T}_o)\right]}_{30}^{80}$= -K ${\left[t\right]}_0^{300}$

${\left[\mathrm{<br>}\right]}_{}^{}$ $\mapsto \frac{2.3026}{K}{\log }_{10}\frac{80-20}{50-20}$= -300

$<br>$ $\mapsto \frac{2.3026}{300}{\log }_{10}2$ = K ….(ii)

The temperature of the body falls from 60 $℃$ $<br>$ to 30 $℃\mathrm{i}\mathrm{n}\mathrm{}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{}=\mathrm{}\mathrm{t}\mathrm{\text{'}}$ $\mathrm{<br>}$

Hence, we get:

$\mathrm{<br>}$ $\frac{2.3026}{K}{\log }_{10}\frac{60-20}{30-20}$ = -t'

$\frac{\mathrm{<br>}}{}$ $\mapsto \frac{-2.3026}{t\text{'}}{\log }_{10}4$ = K....(iii)

Equating equations (ii) and (iii), we get,

$<br>$ $\frac{2.3026}{300}{\log }_{10}2$= $\frac{-2.3026}{t\text{'}}{\log }_{10}4$

$\frac{<br>}{}$ $\mapsto t^{\text{'}}=300\times 2=600s$ = 10 min

Hence, the time taken to cool the body from 60 $℃$ $<br>$ to 30 $℃$ is 10 minutes.

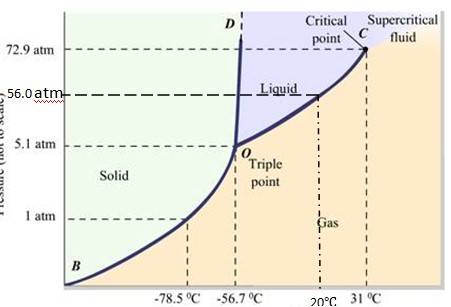
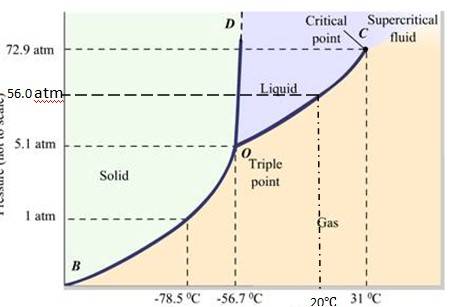
Q.11.21 Answer the following questions based on the P-T phase diagram of carbon dioxide:

(a) At what temperature and pressure can the solid, liquid and vapour phases of CO₂ co-exist in equilibrium ?

(b) What is the effect of decrease of pressure on the fusion and boiling point of CO₂ ?

(c) What are the critical temperature and pressure for CO₂ ? What is their significance?

(d) Is CO₂ solid, liquid or gas at (a) –70 °C under 1 atm, (b) –60 °C under 10 atm,

(c) 15 °C under 56 atm ?

Ans.11.21:

• The P-T phase diagram for CO₂ is shown here. O is the triple point of the CO₂ phase diagram. This means that at the temperature and pressure corresponding to this point, the solid, liquid and vaporous phases of CO₂ exists in equilibrium.
• The fusion and the boiling points of CO₂ decreases with a decrease in pressure.

• The critical temperature and critical pressure of CO₂ are 31 $℃$ 72.9 atm respectively. Even if it is compressed to a pressure greater than 72.9 atm, CO₂ will not liquefy above the critical temperature.

  It can be concluded from the P-T phase diagram of CO2 that:

  CO₂ is gaseous at -70 $℃\mathrm{<br>}\mathrm{<br>}$ , under 1 atm pressure.

  CO₂ is solid at -60 $℃$ , under 10 atm pressure.

  CO2 is liquid at 15  $℃$ , under 56 atm pressure.

 

Q.11.22 Answer the following questions based on the P – T phase diagram of CO₂:

(a) CO₂ at 1 atm pressure and temperature – 60 °C is compressed isothermally. Does it go through a liquid phase ?

(b) What happens when CO₂ at 4 atm pressure is cooled from room temperature at constant pressure ?

(c) Describe qualitatively the changes in a given mass of solid CO₂ at 10 atm pressure and temperature –65 °C as it is heated up to room temperature at constant pressure.

(d) CO₂ is heated to a temperature 70 °C and compressed isothermally. What changes in its properties do you expect to observe?

Ans.11.22

The fusion and boiling points are given by the intersection point where this parallel line cuts the fusion and vaporization curves. It departs from ideal gas behavior as pressure increases.

At 1 atm pressure and at – 60 °C, it lies left of -56.6  $℃$ (triple point O). Hence, it lies in the region of vapour and solid phases. Thus,  CO₂ condenses into solid state directly, without going through liquid phases.

At 4 atm pressure,  CO₂ lies below 5.11 atm (triple point O). Hence it lies in the region of vaporous and solid phases. Thus, CO₂ condenses into solid state directly, without going through liquid state..

When the temperature of a mass of solid  CO₂ ( at 10 atm pressure and at -65 $℃$ is increased, it changes to the liquid phase and then to the vaporous phase. It forms a line parallel to the temperature axis at 10 atm. The fusion and boiling points are given by the intersection point where this parallel line cuts the fusion and vaporization curves.

If CO2 is heated to 70  $℃)$ compressed isothermally, then it will not exhibit any transition to the liquid state. This because 70  $℃\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{}$ is higher than the critical temperature of  CO₂ . It will remain in the vapour state, but will depart from its ideal behavior as pressure increases.