Rachit Kumar SaxenaManager-Editorial
What are derivative?
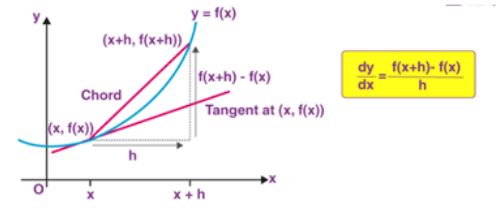
A derivative is the branch of calculus. It is termed as the rate of change of a quantity or a function with respect to other functions or quantity. Calculating the derivative of functions is known as differentiation. The formula for derivative is:
f'(x) = limΔx→0{f(Δx +x)−f(x)}/ Δx
If we have a function p(x), then the symbol of its derivative will be p'(x).
Properties of Derivatives:
If a(x) and b(x) are the functions, then the properties of derivatives will be:
d [a(x) + b(x)] /dx = d(a(x))/dx + d(b(x))/dx
d [a(x) - b(x)] /dx = d(a(x))/dx - d(b(x))/dx
d[a(x) * b(x)] /dx = d [(a(x)* b(x) + a(x)*d(b(x))/dx ] /dx
d/dx [a(x)/b(x)] = {d/dx [a(x)b(x) - a(x)d(b(x))/dx ]} / (b(x))2
Types of Derivatives
There are generally 2 types of derivatives:
First-Order Derivative: It explains the function's direction, whether it is increasing or decreasing.
Second-Order Derivative: This derivative helps in providing the graph's shape for the respective function.
Important Applications Derivatives in Mathematics
Derivatives have various applications in mathematics like:
- Normal and Tangent to a curve
- Newton's Method
- Linear Approximations
- Maximum and Minimum Values
- Increasing and Decreasing Functions
- General Formulas of Derivative:
Some of the general formulas are -
| d(x)/dx = |
1 |
| d(ax)/dx = |
a |
| d(xn)/dx = |
nxn-1 |
| d(sin x)/dx = |
cos x |
| d(cos x)/dx = |
- sin x |
| d(tan x)/dx = |
sec2 x |
| d(cot x)/dx = |
- cosec2 x |
| d(cosec x)/dx = |
- cosec x. cot x |
| d(sec x)/dx = |
sec x. tan x |
| d(ln x)/dx = |
1/x |
| d(ex)/dx = |
ex |
| d(ax)/dx = |
ax(ln a) |
| d(sin-1 x)/dx = |
1/√(1-x2) |
| d(tan-1 x)/dx = |
1/(1+x2) |
| d(sec-1 x)/dx = |
1/(|x|* √x2-1) |
Weightage of Derivative
The topic of derivatives has a weightage of nearly 4 to 6 marks. Around 2 to 3 questions are always asked in class 11th exams, and the questions range from easy to moderate level. The questions of class 12th also use the concept and applications of Limits and Derivatives. The chapter Limits and Derivatives, and its applications are present in both class 11th as well as class 12th. Limits is also a topic from the same chapter; Limit is termed as a value from a function f(x) when f(x) reaches the limit. It is used to define integral calculus, continuity, and
integration of the function. Other topics that are involved in the chapter Limits and Derivatives are:
- Defining Derivatives of a function
- Trigonometric Functions Limits
- Limits and Derivatives
FAQs on Derivative
Q: What is Partial Derivative?
Q: What will be the derivative of a constant?
A: The derivative of constants like numbers, unknown variables is always zero.
Q: Mention one example of Derivatives that exist in the real world.
A: We can use Derivatives for evaluating the profit and loss for an organization with the help of graphs.
Q: What will be the derivative of sinx*cosx?
A: d(sinx*cosx)/dx = cos2x - sin2x
Q: What is the formula for the limit of a function p(x)?
News & Updates
Maths Limits and Derivatives Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test