Triangle: Overview, Questions, Preparation

Triangles are one of the most important topics of mathematics. It studies the similarity of shapes, various theorems detailing a similar relationship between the two triangles. These theorems apply to every type of triangle, starting from an isosceles to a right-angled triangle. 

The following conditions for similar triangles, various similarity criteria theorems of triangles, and results derived from these criteria need to be understood and remember:

Similar Figures

Source: NCERT

Similar Triangles

Two triangles are said to be similar if:

1. Their corresponding sides are in the same proportion (ratio), 
2. And their corresponding angles are equal.

Various Criteria for Similarity of Triangles 

• AAA (Angle-Angle-Angle) Similarity Criteria

Two triangles are similar; if the two triangles' corresponding angles are equal, then their corresponding sides are in the same proportion. 

• AA (Angle-Angle) Similarity Criteria

If the two angles of one triangle are equal to two angles of the other triangle, both triangles are similar.

• SSS (Side-Side-Side) Similarity Criteria 

Two triangles are similar; if the corresponding sides of two triangles are in the same proportion, their corresponding angles are in the same ratio.

• SAS (Side-Angle-Side) Similarity Criteria

Two triangles are similar if one angle of a triangle is equal to the one angle of another triangle, and sides including these angles are in the same proportion.

Results derived from Similarity Criteria Theorems

• The ratio of Corresponding sides = Ratio of Corresponding Medians
• The ratio of Corresponding sides = Ratio of Corresponding Segments of an angle bisector.
• The ratio of Corresponding sides = Ratio of Corresponding Perimeters
• The ratio of Corresponding sides = Ratio of Corresponding Altitudes 

A triangle is a geometrical figure comprising three vertices and three sides. The sum of all angles in a triangle is 180 degrees, and this is the fundamental property of this three-sided figure.

Properties of a Triangle 

The important properties of a triangle, as stated below:

• Every triangle has three vertices and three sides. 
• The sum of all the interior angles of a triangle is equal to 180 degrees. If we consider the exterior angles, this measurement goes up to 360 degrees. 
• In a triangle, the addition of the lengths of two sides is always greater than the third side. Also, the difference of any two sides of a triangle is always less than the third side. 
• The smallest side of a triangle is always opposite to the smallest angle, whereas the largest side of a triangle is always opposite to the largest angle. 

Types of Triangles

Based on its sides’ length, a triangle has three types, viz. scalene, equilateral and isosceles triangle. Based on the measurement of its angles, a triangle has three types, viz. acute-angled triangle, obtuse-angled triangle, and right-angled triangle. 

Based on the sides

• Scalene - A triangle in which all the sides have different lengths.
• Isosceles - A triangle in which any two sides have equal length.
• Equilateral - A triangle in which all the sides have the same length.

Based on the angles

• Obtuse-angled triangle - If one angle of a triangle measures more than 90 degrees, it is an obtuse-angled triangle.
• Acute-angled triangle - If one angle of a triangle measures less than 90 degrees, it is an acute-angled triangle.
• Right-angled triangle - A triangle with one angle that measures up to 90 degrees, is called a right-angled triangle. 

Area & Perimeter of a Triangle 

The area of a triangle can be measured by multiplying the product of its base and height by half. 

Area of a triangle = ½ x base x height. 

The perimeter of a triangle is equal to the sum of its all sides.

Heron’s Formula

If the length of all the sides of a triangle is known, then its area can be measured by using Heron’s formula which says that area of a triangle ABC = √[s(s-a)(s-b)(s-c)], where s = perimeter of the triangle. 

This is an important chapter in class 10. 8-10 marks are allotted to this chapter. A student may expect 1 mark, 2 marks and 3 marks questions from this chapter. 

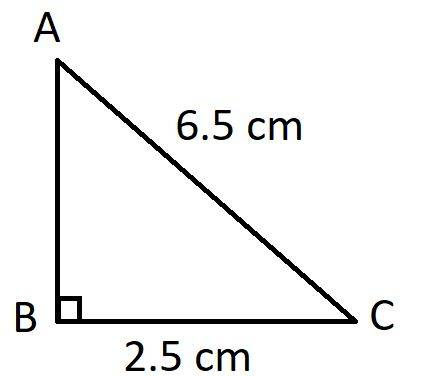
1. A 6.5 m long ladder is put against a wall so that its foot should rest at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it.

Solution: 
Let AC be the ladder and AB be the wall.
Given: AC = 6.5m =13/2 m
BC=2.5 m= 5/2m    
In Right angle triangle, ABC,

AB² + BC² = AC² (By using Pythagoras Theorem)

AB²+ (5/2)² = (13/2)²

AB²= 169/4 – 25/4

AB² = 144/4 = 36

∴Required height, AB = 6 m

2. If a line segment intersects sides AB and AC of an ∆ABC at D and E respectively and is parallel to BC, prove that AD/AB=AE/AC. 

Solution:
Given: In ∆ABC, DE || BC                                                                               

To prove: ∆DAB=∆EAC
Proof: 
In ∆ADE and ∆ABC    
∠1 = ∠1 … Common
∠2 = ∠3 … [Corresponding angles]
∆ADE ~ ∆ABC [AA similarity criteria]  
∴ AD/AB =AE/AC   [In similar ∆’s corresponding sides are proportional to each other.]

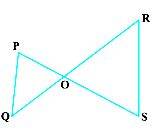
3. If PQ || RS, prove that ∆POQ ~ ∆SOR.

Solution:
PQ || RS (Given)

Source:NCERT
So, ∠ P = ∠ S (Alternate angles) 
∠Q = ∠ R
 ∠∆POQ = ∠∆SOR (Vertically opposite angles)
 Therefore, ∆POQ ~ ∆SOR (AAA similarity criterion)

4. The height of a triangle is 30cm and its base measures 45 cm. Find its area.

Solution:

Area of a triangle = ½ x base x height = ½ x 30 x 45 = 675 square cm. 

5. The perimeter of an equilateral triangle is 120 cm. Find its area. 

Solution:

In an equilateral triangle, each side has the same length. Therefore, if we consider each side to be of length x, then the perimeter can be given by:

3x = 120. 

Therefore, x = 40. 

From Heron’s formula the area of the triangle will be:

= √[s(s-a)(s-b)(s-c)]
= √[ 120 (120 - 40) (120 - 40) (120 - 40)]
= √[120 x 80 x 80 x 80]
= 5608679 square cm. 

6. In triangle ABC, AB = 5cm and BC = 7cm. Find the length of its other side if its perimeter is equal to 15cm. 

Solution:

Perimeter = sum of all sides = AB + BC + AC

15 - (5 + 7) = AC 

Therefore, AC = 3 cm.

Q: What is Thales Theorem?

Q: What is the converse of the Triangle Proportionality Theorem?

Q: Explain Angle Bisector Theorem?

Q: Explain Pythagoras Theorem?

Q: Explain Converse of Pythagoras Theorem?