Pythagoras Theorem: Overview, Questions, Preparation

The Pythagoras theorem states that “the area of the square of the hypotenuse in a right angle triangle is equal to the sum of the area of the square of the other two sides. Evidently, the 3 main sides of a right-angled triangle are known as the ‘Perpendicular’, ‘Base’, and ‘Hypotenuse’, where ‘hypotenuse’ is considered to be the longest since it is opposite to the 90-degree angle.

Pythagoras Theorem: Derivation 

We take a right-angled triangle ABC, with ∠B being 90°, where line BD is drawn perpendicular to hypotenuse AC, giving rise to triangle ADC. On comparing ADC and ADB,  

We know that ΔABC ~ ΔADB 

Hence, AD/AB = AB/AC (since they’re opposite sides of both Δs) 

AB²=ADxAC…….(i)
And, ΔBDC ~    ΔABC

BC²=CDxAC…….(ii)

Add equations (i) & (ii) 

AB²+BC²= ADxAC+ CDxAC

AB²+BC² = AC (AD+DC)
AD+CD = AC;
Hence, AC² = AB² + BC²

Pythagoras Theorem: Formula 

The Pythagoras theorem formula states that - 

Here ∠A is perpendicular, whereas ‘∠B is the base and ∠C is the hypotenuse. 

As per definition, Pythagoras theorem is derived from - 

Hypotenuse² = Perpendicular²+ base² 

 a²+b² = c²

Pythagoras theorem is one of the most interesting topics covered in the Geometry unit under the Class 10 ICSE syllabus alongside circles and construction. The Pythagoras theorem usually carries a total weightage of 15 marks in the question paper of 80 marks. 

Illustrated Examples on Pythagoras theorem

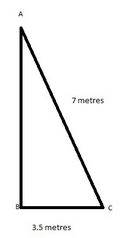
1: A platform ladder is placed against the wall with its foot at a distance of 3.5m & the top reaching a door above the ground at a distance of 7m. Find the length of the ladder. 

Solution:

Here AB is the platform and CA is the wall, where A is the window. 

BC = 3.5m 
CA = 7m 
Using Pythagoras theorem, 
AB² = BC²+CA² 
=1.87+49= 50.87 
AB = 7.13m

2: Find hypotenuse of a triangle with 2 sides measuring 9 cm & 5 cm.

Solution:

Hypotenuse² = Perpendicular²+ Base² 

Hypotenuse² = (9)²+ (5)²
 
                = 81+25 = √106 
                 = 10.29 

3: In a right-angled triangle, the hypotenuse is 12 cm and another side is 4cm, find the third side. 

Solution:

Hypotenuse² = Perpendicular²+ Base² 

\(a^{2}=b^{2}+c^{2}\)

\(12^{2}=4^{2}+c^{2}\)
\(c =\sqrt{12^{2}-4^{2}}=\sqrt{144-16}= 128 = 11.3 cm 

Q: What is Pythagoras theorem’s formula? 

Q: For which type of triangles can the Pythagoras theorem be applied? 

Q: How can I obtain the length of a triangle? 

Q: Which is the longest side of a right-angled triangle? 

Q: What is the formula to find the length of a hypotenuse?